[Paper Review] Understanding Dimensional Collapse in Contrastive Self-Supervised Learning
Paper Review
Understanding Dimensional Collapse in Contrastive Self-Supervised Learning

병리 이미지 특성 상 labeling 에 들어가는 비용이 높기 때문에 이 분야에서는 self-supervised learning 이 심심치 않게 사용된다. BYOL, SimCLR, MoCo 등의 논문을 보면 collapse를 막기 위해 이 방법을 사용했다 라는 statement를 자주 볼 수 있다. 이번 포스팅에서는 ICLR 2022에 억셉된 paper를 통해 dimensional collapse 가 무엇인지, 기존 모델의 구조는 어떻게 dimensional collapse 를 막았는지 등에 대해 정리해보려 한다.
Introduction
Self-supervised visual representation learning은 human annotation의 도움 없이 embedding space에 유용한 representation을 배우도록 해준다. Joint embedding approach 는 다른 view로 본 같은 image 사이의 거리를 minimizing 하는 방식으로 학습하는데, 이는 적절한 보완이 없다면 모델이 trivial constant solution 을 내놓는 문제, complete collapse problem을 야기할 수 있다. Contrastive learning 의 경우 negative sample과 positive sample의 repulsive effect를 통해 이 문제를 완화하는데, 그럼에도 embedding vector가 특정 dimension으로 표상되는 dimensional collapse 문제가 발생한다. 저자는 dimensional collapse를 야기하는 contrastive learning의 dynamic을 관찰하고 두 가지 원인을 제안, 분석하여 새로운 contrastive learning method DirectCLR 를 제안한다.
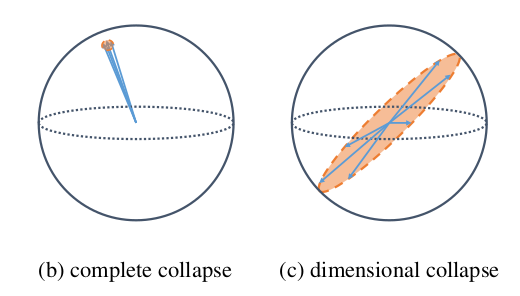
we summarize our contributions as follows:
- We empirically show that contrastive self-supervised learning suffers from dimensional collapse whereby all the embedding vectors fall into a lower-dimensional subspace instead of the entire available embedding space.
- We showed that there are two mechanisms causing the dimensional collapse in contrastive learning: (1) strong augmentation along feature dimensions (2) implicit regularization driving models toward low-rank solutions.
- We propose DirectCLR, a novel contrastive learning method that directly optimizes the representation space without relying on an explicit trainable projector. DirectCLR outperforms SimCLR with a linear trainable projector.
Self-supervised Learning methods
Joint embedding 방식은 training instance에 다른 augmentation을 적용하고 이들의 representation space 상의 거리가 가깝도록 표상하는 방식이다. Contrastive methods는 각 sample이 own class로 정의되고 그 이외의 것은 모두 negative sample로 정의되며, 보통 InfoNCE contrastive loss 를 기반으로 학습된다. In practice, CL 방식은 많은 수의 negative sample이 필요한 것으로 알려져 있다. Non contrastive methods는 clustering based method, redundancy reduction methods, methods using special architecture design 등을 포함한다.
underlying dynamics of SSL methods remains poorly understood
- theoretically proved that the learned representation via CL are useful for downstream task
- explained why non-CL methods like BYOL and SimSiam work
: the dynamics of the alignment of eigenspaces between the predictor and its input correlation matrix play a key role in preventing complete collapse
Implicit Regularization
기존 연구 결과, linear neural network setting 에서 gradient descent 가 adjacent matrices alignment 상황을 초래하고, 이 setting 에서 gradient descent 가 minimal nuclear norm solution 을 derive 함이 보여졌다. 나아가 deep linear network can derive low-rank solution 임을 이론적으로, 실험적으로 증명하였다. In general, over-parameterized neural networks tend to find flatter local minima.
Dimensional Collapse
CL methods prevent complete collapse via the negative term that pushes embedding vectors of different input images away from each other. 하지만 complete collapse를 막음에도 여전히 dimensional collapse 문제가 있음을 다음 실험으로 확인함.
- train SimCLR model with a two layer MLP projector
- standard recipe and trained the model on ImageNet for 100 epoch
- evaluate dimensionality by collecting embedding vector in validation set (d=128)
- covariance matrix of embedding layer and do SVD
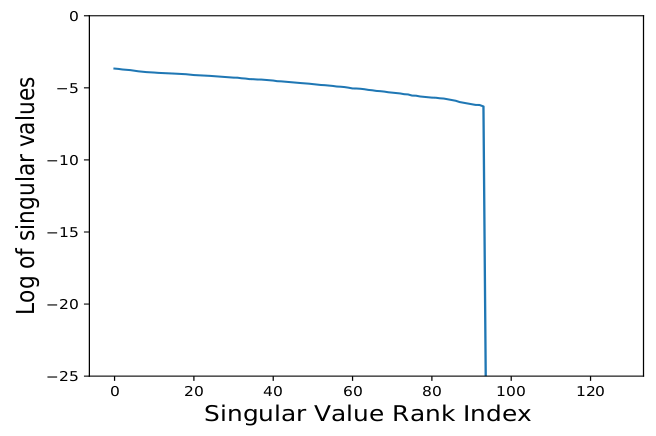
: we observe that a number of singular values collapse to zero, thus representing collapse dimensions
two difference mechanisms that cause collapsing
1) along the feature direction,, where data augmentation 에 의한 variance가 data distribution 자체의 variance 보다 클 때, weight collapse.
2) augmentation 에 의한 영향이 적더라도, interplay of weight matrices at different layers (implicit regularization) 에 의해 weght will still collapse.
Dimensional Collapse caused by Strong Augmentation
explained one scenario for CL to have collapsed embedding dimensions, where the augmentation surpasses input information.
- simple linear network 에 초점을 맞춤.
- intput vector as x, augmetation is an additive noise
- focus on typical CL loss, InfoNCE
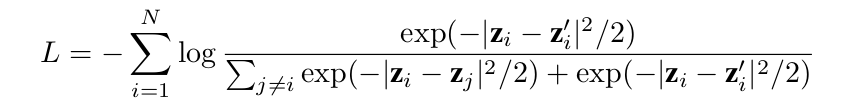
zi, zi' : pair of embedding vectors / zj : negative samples within minibatch
Gradient flow dynamics
We study the dynamics via gradient flow, i.e., gradient descent with an infinitesimally small learning rate.
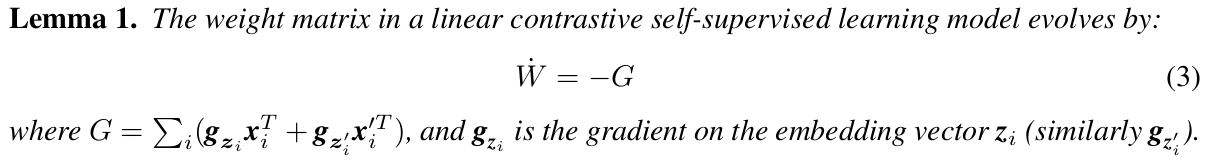
증명과정은 chain rule을 통해 설명될 수 있다. 이 때, InfoNCE loss를 통해 gradient를 써서 이리저리 수식을 정리해보면 다음과 같은 관계식을 도출해낼 수 있다.

또한 G 를 표현하고 있는 X 는 수식을 정리했을 때, weighted data distribution vocariance matrix 와 weighted augmentation distribution covariance matrix의 차이로 표현된다.
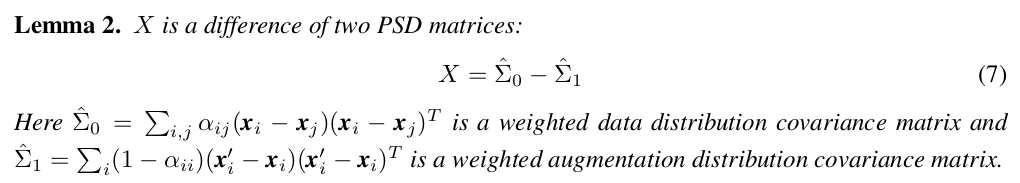
식을 잠시 들여다보면, X는 two PSD matrices (covariance matrices는 PSD) 의 차이로 표현되고, 이를 이용해 제안한 첫번째 mechanism 대로 augmentation 의 크기를 크다라고 가정한 뒤 weight matrix W 의 dynamic을 관찰할 수 있게 된다.
Theorem 1. With fixed matrix X (defined in Eqn 6) and strong augmentation such that X has negative eigenvalues, the weight matrix W has vanishing singular values.
증명을 간단히 설명하자면, lemma 1에 의해 이고, eigen decomposition에 의해 로 표현 가능하고, X가 negative eigenvalues를 가지고 있다 했으므로 t가 infinite로 갈 때, W(inf)도 rank deficient이므로 weight matrix W 가 vanishing singular value를 가진다 설명할 수 있다. 따라서,
Corollary 1 With strong augmentation,the embedding space covariance matrix becomes low-rank.
(covariance matrix 식의 weight가 rank deficiency를 띄므로 C 또한 low-rank, indicating dimensional collapse.)
또한 numerical simulation을 통해 이론적 증명을 확인하려는 시도를 거쳤다. augmentation 을 additive Gaussian with covariance matrix 로 잡고, k (augmentation 세기) 의 크기를 늘리면서 singular value rank index를 확인하였다.
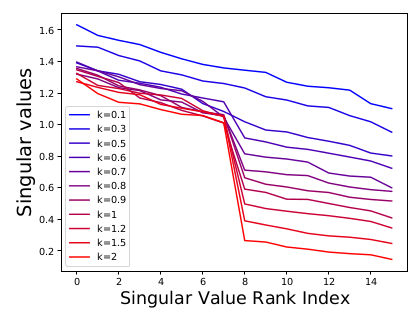
이는 linear network setting 에서 strong augmentation 이 embedding space 상의 dimension collapse 를 야기함을 보여준다.
Dimensional Collapse caused by Implicit Regularization
strong augmentation이 없을 땐 X matrix는 PSD 이고 논리대로 라면 single linear model은 dimensional collapsing이 없어야 한다. 하지만, deep network 상에선 여전히 dimensional collapsing이 발생하였고, over-parametrized linear network가 low-rank solution을 찾으려는 경향인 implicit regularization 측면에서 설명하고자 하였다.
- two-layer linear MLP without bias (simple over-parameterized setting)
- intput vector x, augmentation is additive noise
- , not normlized z
- used InfoNCE loss, basic SGD without momentum or weight decay

Gradient flow dynamics

strong augmentation 에서의 과정과 비슷하게, two linear layer setting 에서의 weight 변화를 표현하였고, 이에 InfoNCE loss 를 적용하여 수식을 정리하여 위와 같이 식을 정리하였다. 이 때, augmentation이 강하지 않다는 설정을 통해 X 가 PSD 라는 조건도 가져갈 수 있다.
Weight alignment
Implicit regularization은 explicit regularization 과 달리 별도의 penalty term이 없음에도 불구하고, deep network 에서 서로 다른 layer의 weight 의 interplay 로 인해 모델이 low-rank solution 을 찾으려는 tendency 를 의미한다. 이를 확인하기 위한 첫번째 질문은 "how they interact with each other?"이다. 와 사이의 interaction을 보기 위해 SVD로 쪼개었고, A라는 alignment matrix 을 중심으로 증명을 전개했다.

Theorem 2. If for all t, is positive-definite and , have distinctive singular values, then the alignment matrix .
증명 과정을 간단히 요약하면, lemma3를 이용하여 와 의 변화량이 같음을 보이고, 식과 (Frobenius norm을 통해 weight matrix가 grow to infinitely 상황을 가정) 상황을 통해 을 보여 , 를 보인다.

또한 실험적으로 absolute value of the alignment matrix A가 identity matrix I로 수렴함을 보인다. (real scenario에선 alignment matrix가 block-diagonal matrix로 수렴함을 확인, 각 block은 representing group of degenrate singular values)
이제 위를 통해 증명한 "singular vectors corresonding to the same singular value align" 이라는 명제를 통해, 각 weight matrix의 dynamic을 관찰할 수 있게 되었다.
Therorem 3. If and are aligned (i.e., ), then the singular values of the weight matrices and under InfoNCE loss evolve by:
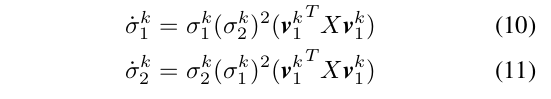
따라서 (10), (11)과 같은 식이 성립함을 알 수 있다. 해석하자면, pair of singular values (same ranking을 가진 서로 다른 weight layer의 singular value, sig1^k, sig2^k) 의 gradient는 proportional to themselves 한다는 것을 알 수 있다. 이 때 X는 항상 PSD 이고, v1 어쩌구 식도 항상 non-negative 이다. 따라서 위 식들은 왜 the smallest group of singular value가 확연하게 느리게 grow 하는지 설명해준다.

Corollary 2 With small augmentation and over-parametrized linear networks, the embedding space covariance matrix becomes low-rank.
corollary 1 과 마찬가지로, embedding space는 embedding vector의 covariance matrix의 singular value spectrum에 의해 정의되므로, 가 evolves to low-rank 라면 C도 low-rank, 즉 dimensional collapse이 일어남이 설명된다.
DirectCLR
motivation
앞선 theoritical finding을 바탕으로 novel algorithm을 제시한다. 실험적으로, "projector" 를 뒷단에 추가하는 것이 learned representation 의 quality 와 downstream performance 를 향상한다는 연구 결과가 있었다. (SimCLR의 projection head는 none->linear->nonlinear 순으로 성능이 높아졌던 바 있음.) 이 논문에서도 앞선 방법을 적용하여 singular value rank spectrum 을 관찰하여, 실제로 projector의 유무가 dimensional collapse에 중요하다는 결과를 얻는다.
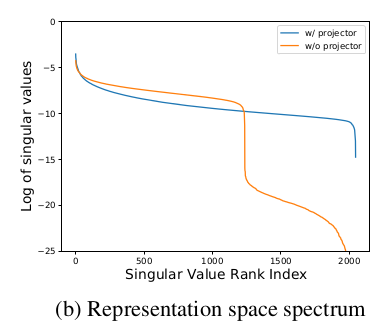
이를 바탕으로, contrastive learning에서의 projector 가 어떤 메커니즘으로 dimensional collapse 를 막는지에 대한 proposition 2개를 제시한다.
Proposition 1. A linear projector weight matrix only needs to be diagonal.
Implicit regularization 파트에서 보였듯, adjacent layer 간 alignment로 dynamic은 각 weight matrix의 singular value , 에 의해 결정된다. 또한, 방향으로 evolve 하기에, orthogonal matrices (, )는 redundant 하다.
여기서 linear projector SimCLR model 을 생각해 봤을 때, 을 encoder의 last layer, 를 projector weight matrix 라 치면, 이 사람들은 의 orthogonal component인 는 생략될 수 있다 주장한다. layer 이 fully trainable 하면 align 되는 방향으로 가서 결국 의 orthogonal component인 는 방향으로 학습될 것이기에, final behavior of projector는 singular values ()에 의해서만 결정될 것이라는 주장이다. 이를 통해 weight의 orthogonal component는 크게 중요치 않고 diagonal matrix 만이 (prevent dimensional collapse에) 영향을 미칠 것이라는 내용의 proposition 1 을 제안한다.
Proposition 2. A linear projector weight matrix only needs to be low-rank.
또한 저자는 weight matrix will always converge to low-rank 임을 dynamic을 통해 설명한 바 있다. (앞선, encoder가 W1이고 projector의 앞단이 W2라는 가정은 잠시 잊자.) 여기서, singular value diagonal matrix 가 naturally becomes low-rank 되는 현상이 있으므로, 아예 처음부터 low rank로 set 해버리면 어떻겠냐는 제안을 한다.
Also, according to our theory, the weight matrix will always converge to the low-rank. The singular value diagonal matrix naturally becomes low-rank, so why not just set it low-rank directly? This is the motivation of Proposition 2.
위 두 proposition 이 맞는지 아래 실험을 통해 확인하고자 하였다.
main idea
DirectCLR은 projector의 어떤 구조(성분)가 prevent dimensional collapse에 영향을 주는지 확인하기 위해, projector 없애고 대신 projector의 일부 구조(성분)만 이용하여 directly optimizes representation space 를 하고 성능을 확인한다.
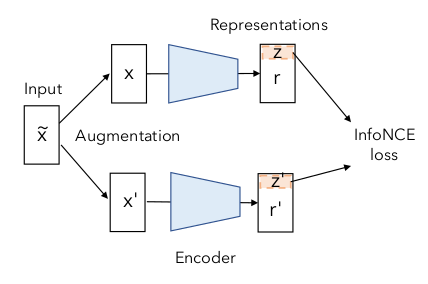
특히 위 그림에서 보이듯, DirectCLR은 representation z에서 subvector를 pick 하는 방법을 제안한다.

Table 1 과 Figure 9 에서 볼 수 있듯이 SimCLR 에서 projector 구조가 없을 때엔 dimensional collapse 가 일어나고, projector 구조가 없어도 DirectCLR - picking subvector 방식을 사용하면 dimensional collapse 가 완화되는 것을 확인할 수 있다.

마지막으로 ablation study 를 통해 proposition 을 검증한다.
Conclusion
위 논문에서는 contrastive self-supervised learning 가 겪는 dimensional collapse 문제에 대해 규명하고, 이를 야기하는 두 가지 메커니즘을 제안하여 이론적으로, 실험적으로 증명하였다. 또한 이론적 토대를 바탕으로 DirectCLR 모델, trainable projector 없이 representation space 를 directly optimize 하는 방식을 제안하여 SimCLR with a linear projector 를 outperform 하는 결과를 도출함.
와 재밌다
