Learning efficient task-dependent representations with synaptic plasticity

• constructed stochastic RNN using novel form of reward-modulated Hebbian synaptic plasticity
• compared each hidden unit activity in two different tasks
• analyzed effects of noise

Task-dependent synaptic plasticity

Stochastic circuit model

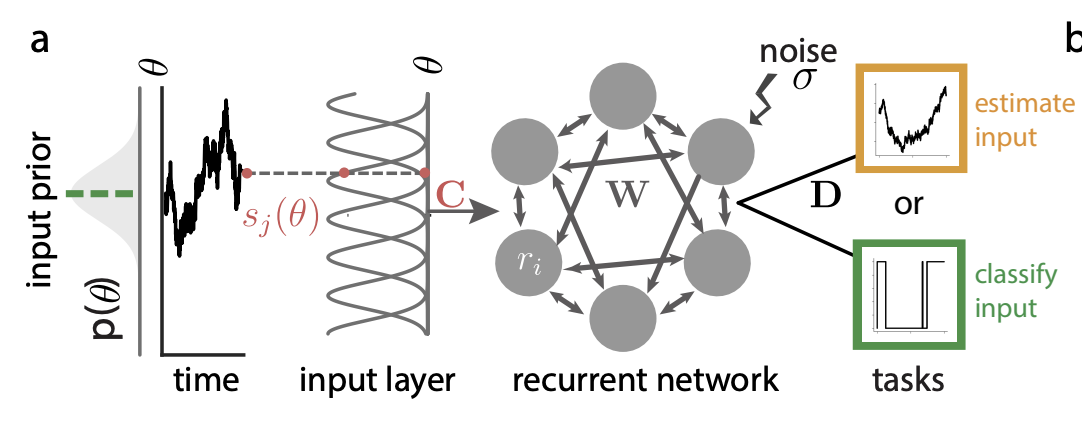
• stimuli orientation theta is drawn from von Mises distribution
• each neuron has fixed tuning s_j(theta)
• estimation task: replicate the input theta / classification task: classify theta >0 or not

The stochastic dynamics governing the activity of recurrent neurons

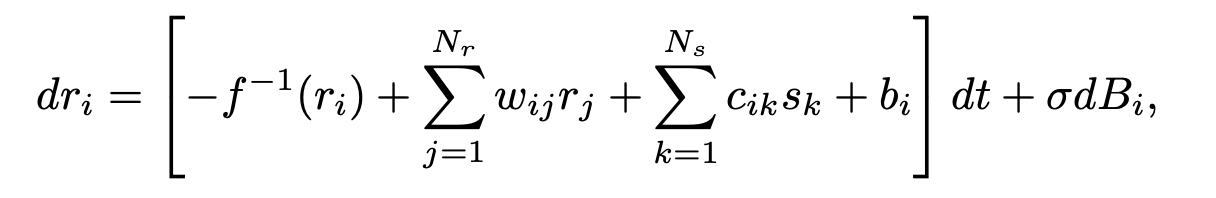
f: nonlinear fuunction.
if we consider steady-state dynamics, at equilibrium,

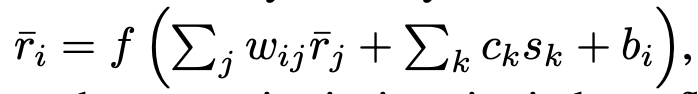
and you could see the origin form of the stochastic dynamics.
Also the Brownian noise B_i added independently to each neuron, and in terms of steady-state dynamics, this noise induces fluctuations about this fixed point (steady-states).

When the recurrent weight W is symmetric, the energy function.

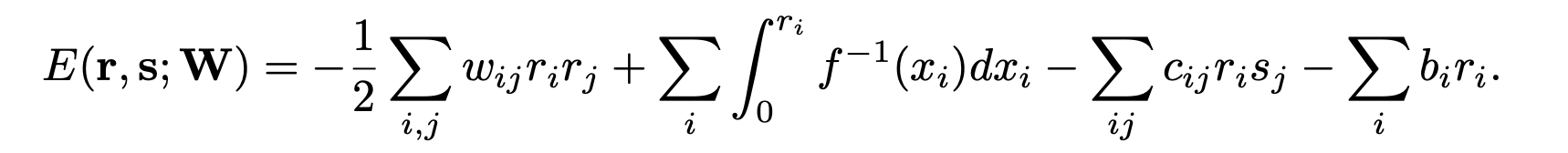
the network dynamics implement SGD on this energy function, which corresponds to Langevin sampling from the stimulus-dependent steady-state probability distribution.

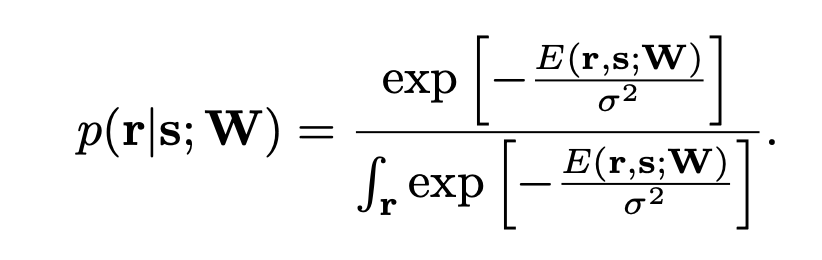
Instead of using backpropagation, they used Langevin sampling (or using Euler-Maruyama integration) for the update.
(d_ri) = -∇E (direction energy diminishing) + noise
--> network sampling with repect to this energy function and the gradient can be approximated with calculating the SDE

https://github.dev/colinbredenberg/Efficient-Plasticity-Camera-Ready

Task dependent objectives

Task-specific objective function

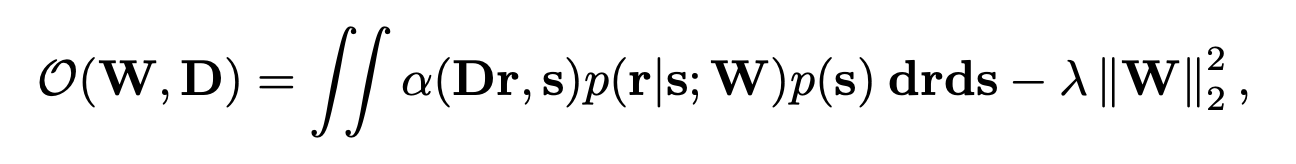
Dr: readout, alpha: task specific loss (cross entropy or MSE)

Local task-dependent learning

They derived synaptic plasticity rules by maximizing O using gradient ascent.

Suggested weight update is similar to a standard reward-Hebbian plasticity rule. (in that, alpha(Dr, s): reward, and rirj-terms: pre-, post-synaptic activity)

Learning the decoder

p(r|s;W) does not depend on D

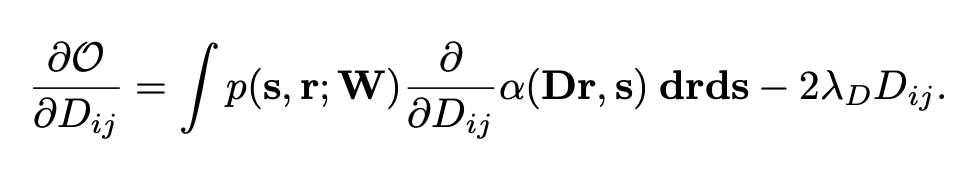
Numerical results

stimulus encoding

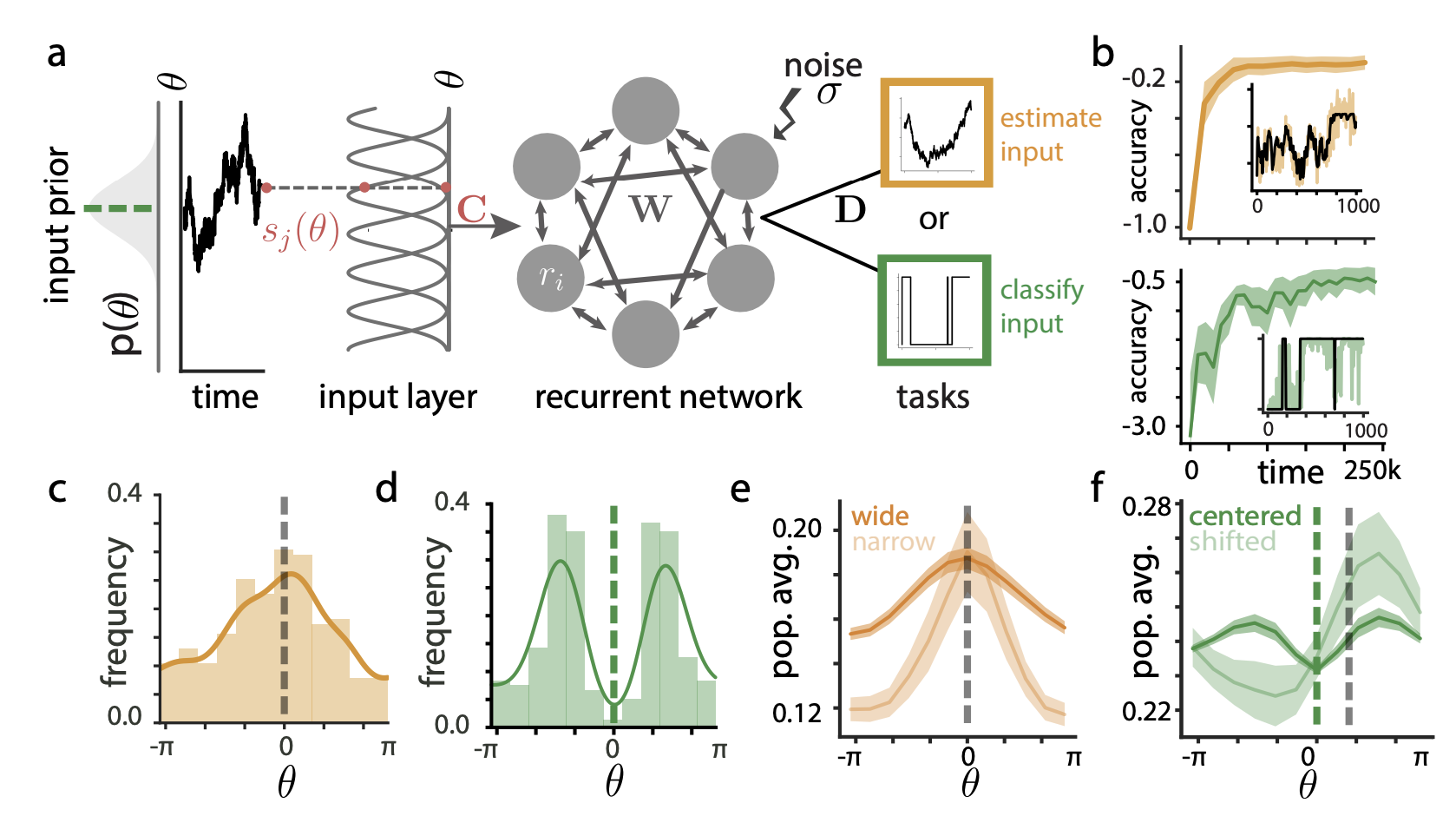
figure1: Recurrent neural network architecture and task learning
figure1b : derived local plasticity rules quickly converge to good solution

figure1c and d: distribution of preferred orientation for each neuron (histogram)

• estimation: concentrated highly probable stimulus
• classification: bimodal

figure 1e and f: average population activies
: encoded prior probability

tested narrower input theta distribution on estimation task, prior encoded.
shifted prior theta distribution in discrimination task --> break symmetricity

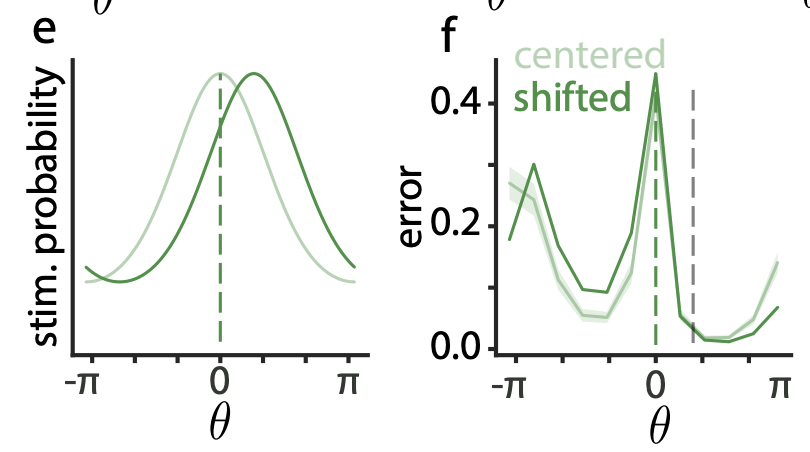
supplementary results, f: broken symmetricity on shifted exp condition.

decoded outputs

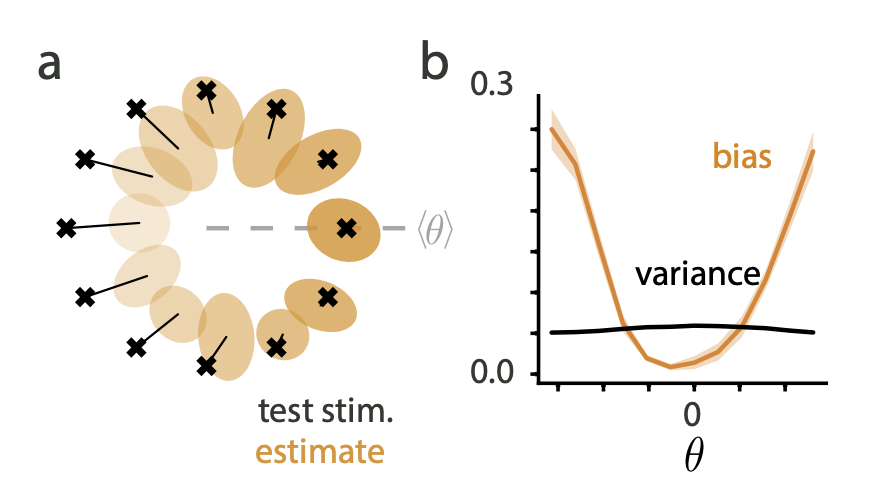
• responses are systematically biased for less probable stimuli.
• effect of variance was much weaker.

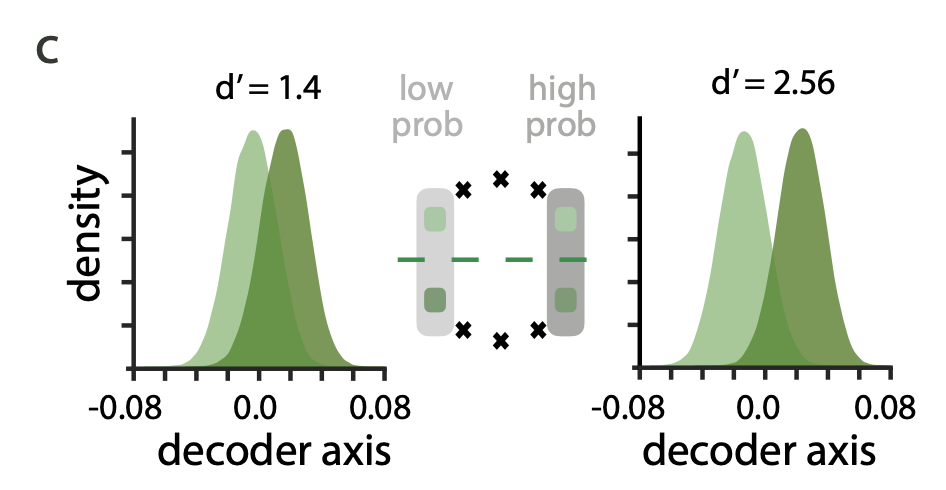
left: theta nearby pi (less probable region), right: theta nearby 0 (most concentrated region)
d': sensitivity index, discriminability

• high discriminability in high probability stimuli region.
  

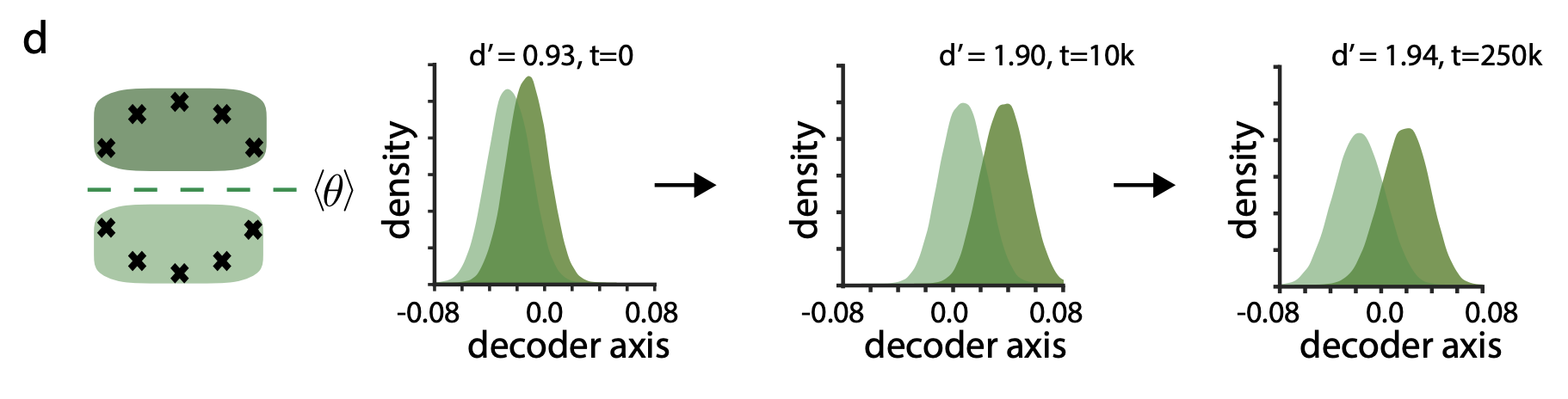
discriminability increased as evidence cumulated

effects of internal noise

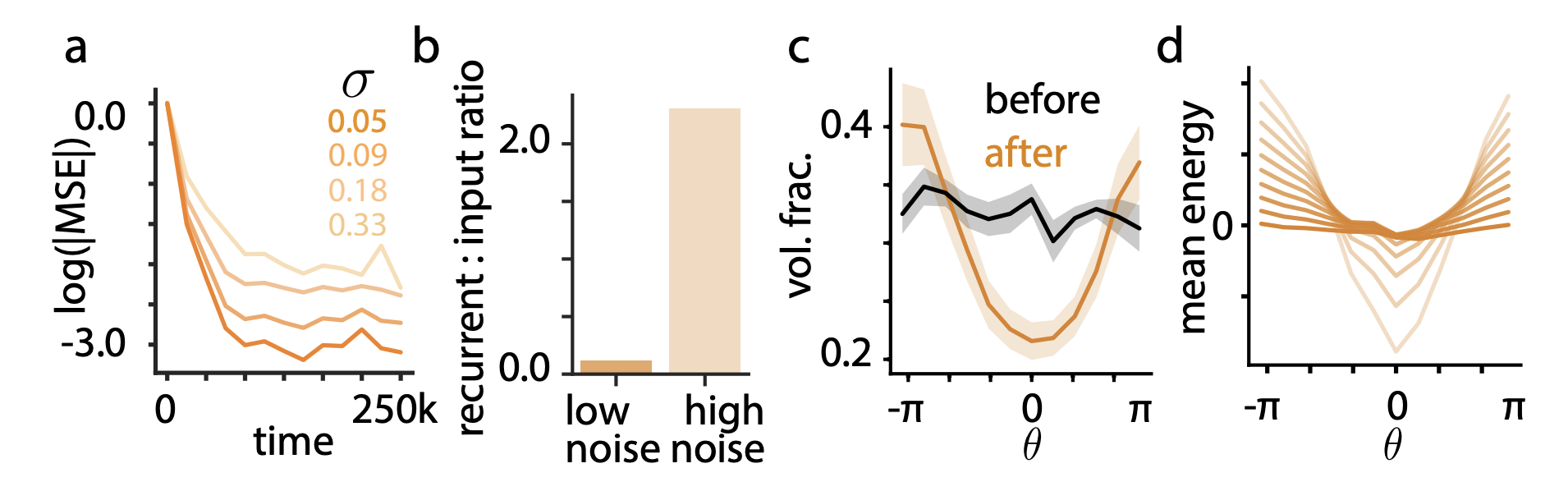
a: increased noise leads to slower learning, worse asymptotic performance
b: higher noise increased engagement of recurrent connectivity after learning. (meaning more bias on previous observations?) - exploit encoded prior distribution more (?)

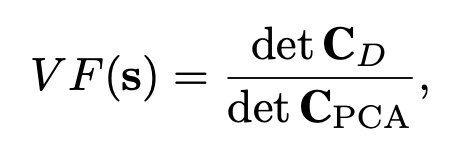
• noise volume fraction (calculated by covariance matrix of r projected onto the two output diensions and covariance matrix of r projected on to the two principal components of the neural activity in fixed stimulus s)

c: after learning, VF much smaller for probable stimulus --> network has learned to effectively "hide" more of its noise for frequent input. (!!) resilient for noise in probable stimulus region

d: interms of energy function, noise variance acts as a temperature. energy landscape "flattens" with increasing noise.

Thoughts

This paper was really inspiring. Although its focus is slightly different from ours—since it proposes a network trained only with local learning rules and analyzes tuning curves and the effects of noise, I thought it would be interesting for us to consider using this model or introducing stochasticity to examine the influence of noise.

Also, the observation that bias increases for improbable stimuli was consistent with my own results. I really liked how they plotted the argmax frequency histogram for each neuron and the average population activity. It gave me the idea that, in our case, it could be valuable to plot neuronal activity across different within-trial steps (steps 0 to 11). My intuition is that there might not be neurons that respond specifically to individual steps, but rather, there may be a directional dynamic that pushes activity forward across the trial.

I also think it would be interesting to plot the recurrent-to-input ratio at each step. Since our task is an integration task, my intuition is that the recurrent contribution should naturally become more dominant in the later steps of each trial.