[Paper Review] Learning Efficient Coding of Natural Images with Maximum Manifold Capacity Representations (WIP)
Paper Review
Learning Efficient Coding of Natural Images with Maximum Manifold Capacity Representations

개인적으로 팔로우 하고 있는 computational neuroscience 분야 정수연 (SueYeon Chung) 교수님 연구실에서 나온 연구이다. 교수님의 2018년 paper Classification and Geometry of General Perceptual Manifolds 에서 manifold capacity 및 manifold dimension & radius framework 가 처음 연구되었고 2020년 center correlation 과 관련된 저서 (Nature comm) 와 함께 visual, language, auditory 분야에서 separability 및 geometry 가 연구되었었다. 이번 연구에서는 manifold capacity framework 에 기반하여 새로운 contrastive learning framework, Maximum Manifold Capacity Representation (MMCR) 을 제안하였다.
정수연 교수님의 저서 An Information-Theoretic Understanding of Maximum Manifold Capacity Representations 내용이 대거 포함되어 있다.
Introduction
위에서 언급했던 대로, 2018년 geometry (size & dimensionality) of neural representation 과 linear decoding capacity 를 연결짓는 새로운 이론, Manifold capacity theory 가 고안되었고, 여러 modality 에서 검증되었다. 하지만 이러한 접근은 데이터를 평가하고 brain function 을 이해하는 방법으로써 연구되어왔고, constructive usage 에 대해서는 덜 연구되어 왔다. 본 연구는 다음 내용을 처음으로 demonstration 하였다.
- optimizing a network for manifold capacity (MMCR) results in good representation for object recognition, when evaluated using the stadard linear evaluation paradigm. approximately matched recent SSL methods
- examining the learning signal reveals the mechanism underlying the emergence of semantically relevant features from data
- MMCR renders interpretable geomteric properties that result in increased robustness to adversarial attack
Related Work
closely related to recent advances in contrastive SSL, but has diff motivation and formulation
- maximize the mutual info btw augmented representations (diff view, same object) --> estimating mutual info is difficult
- SwAV 에서 multi-crop 전략 사용한 것과 비슷하게, different views of image form continuous manifold 라는 가설을 설정.
- point 간의 distance or similarity 를 사용하지 않고, characterize each set of image views with the spectrum of singular values of their representations, using the nuclear norm as a combined measure of the manifold size and dimensionality (geometry)
- 특히 nuclear norm 사용하여 InfoNCE loss 의 regularizer 로서 사용, high rank likelihood 사용 --> discourage dimensional collapse
- encouraging maximal rank --> simplex equiangular tight frame (sETF) representation.. (이 부분은 공부가 필요함)
- spectral decomposition of the population augmentation graph -> SSL objective 로 발전되었는데 이런 approach 도 사용. (잘 몰라서 공부 필요함..)
Maximum manifold capacity representations
Manifold Capacity Theory
D dimensionality 를 가진 feature space 에 embed된 P개의 manifolds (각각은 class label) 가 있다고 생각할 때, manifold theory 는 "what is the largest value of such that there exists a hyperplane separating the random dischotomy?" 라는 질문에 답하고자 한다. 위에서 언급했던 2018년 연구에서 의 upper bound 인 를 manifold capacity 로 정의하고 existence such that when the probability of finding a separating hyperplane is approximately 1.0, and when the probability is approximately 0.0. 임을 증명하였다.
Models of Manifolds
이 연구에 대한 이해가 반드시 필요하다고 생각하기 때문에 잠시 언급하겠다. P 개의 manifold 안에는 같은 class 에 해당하는 여러 data point 들이 있고, neural network 라는 w 로 parameterization 된 함수를 사용하여, 저 P개의 manifold 를 separate 하도록 train 된다고 생각할 때, 먼저 w 의 solution space의 부피를 계산한다. Gardner's framework 에 기반하여 statistical average of log Z, where Z is the volume of the space of the solutions 를 다음 처럼 계산한다.

이 식을 이해하기 위해 기본 setting 에 대해 설명하면 다음과 같다.
각 manifold 는 1~P개의 compact subset of an affine subspace of with affine dimension D with D<N. point of manifold 는 아래와 같이 parameterize 된다.

는 set of orthonormal bases of the (D+1)-dimensional linear subspace containing . 그리고 는 coordinate of manifold point 이고, 라는 큰 set 의 element인 set 에 의해 constrain 된다. 큰 set 자체는 manifold 의 shape 를 결정 짓고, 가정상으로 모든 manifold 에 적용되도록 한다.
두개의 binary label 을 separate 한다는 설정 하에, margin kappa 에 대해 hyperplane 은 모든 에 대해 다음 조건을 만족한다.
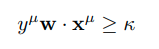
linear separability 는 convex problem 이기 때문에, manifold 를 나누는 것은 convex hull conv() 를 나누는 것과 같고, 이는 다음과 같이 작성할 수 있다.
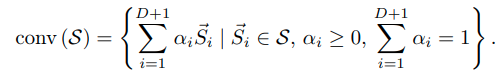
또, affine subspace 의 position 은 origin 과 가장 가까운 translation vector 로 정의될 수 있는데, 이 orthogonal translation vector, 는 의 affine displacement vector 와 모두 수직이고, 그렇기에 아래 사진과 같이, subspace 상 vector와도 모두 수직관계가 성립한다.
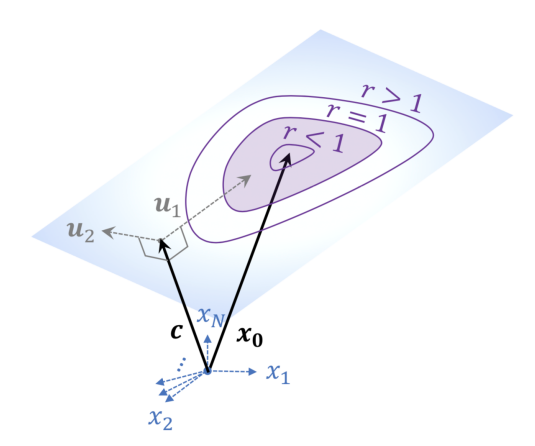
separability propoerties of manifolds 를 조사하기 위해서 shape changing 없이 r 이라는 scaling factor 를 도입하였다. 는 big set S 의 element 이자 각 의 center 이다.
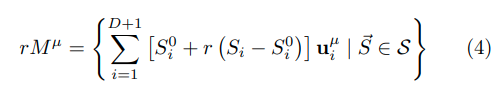
r 이 0으로 수렴할 때 도 point 로 수렴하고, r 이 무한대로 발산할 때 는 affine subspace 전체를 span 하게 된다.
Bounds on linear separability of manifolds
조금 다른 이야기로 넘어와서 Bounds on linear separability of manifolds 에 대해 설명한다. dischotomies of P input points in at zero margin 은 다음과 같다.
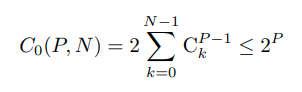
이 때 주목할 점은, 충분히 큰 P 와 N 에 대해서, P = 2N 즉 일 때 sharp transition 이 일어난다.
또한 scaling factor r 이 0으로 수렴할 때와 무한대로 발산할 때의 상황을 고려했을 때 다음과 같은 relationship 이 성립한다.
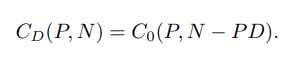
이 relationship 에 기반하여, D-dimensional affine subspace 상에서의 linear separability 는, 충분히 큰 P 와 N 에 대해서, 아예 불가능 -> 모두 가능 을 결정 짓는 critical ratio 를 보인다. finite size 를 가진 D-dimensional manifolds 에 대해, dischotomies (linear separable) 의 lower bound 와 upper bound 는 각각 Cd(P,N), C0(P,N) 이 될 것이고, 여기서 manifold capacity 를 의미하는 가 정의된다. 이는 maximal load such that randomly labeled manifolds are linearly separable with a margin 이다. 위에서 정의한 식에 따라 이 alpha 의 inverse 는 다음과 같은 부등식을 만족하게 된다.
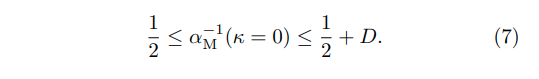
저자는 위와 같이 bound 된 식을 통해, manifold 안에 무한한 점이 존재한다고 하더라도, the maximal number of separable finite-dimensional manifolds 는 N과 비례한다고 언급한다. 이는 이 다음 언급될 statistical mechanical evaluation of the maximal alpha 에 대해 다룰 수 있도록 한다.
Statistical Mechanical Theory
몇가지 가정을 추가한다. individual component of 는 zero mean, 1/N variance 의 Gaussian distribution 으로부터, label y 도 random하게 독립추출된다. N과 P 가 P/N=alpha 라는 finite load 를 만족하면서 동시에 infinite 로 발산한다는 thermodynamic limit과 함께, equation (7) 은 아래와 같이 margin kappa 에 대해 generalize 될 수 있다.

위 식에서 부등식을 만족하는 공간이 overly loose 하기 때문에, 저 양을 잘 estimate 하고 capacity 와 natureo f the solution on geometrical properties of the manifolds 간의 dependence 를 잘 평가하는 것이 중요하다.
Mean field theory of manifold separation capacity

그 사이의 volume of the space of the solution 을 위와 같이 쓸 수 있다. 그 후에 maximum margin solution with fixed kappa 혹은 given alphaM 상황에서의 maximum margin kappa 에 대한 solution 을 계산하고자 하였다. 위에서 언급했던 P/N = constant, P, N -> infinite 라는 thermodynamic limit 을 적용했을 때 general form of the inverse capacity 를 다음과 같이 구하였다. (appendixA 참조)

조금 더 부연설명을 하자면, vector V 는 separability 를 만족하는 vector 를 의미하고, random 하게 sample 된 T 들에 대해 가장 가까운 V 들의 average 를 구한 것이 inverse capacity 라고 이해할 수 있다. 다르게 작성하면 아래와 같이 작성할 수도 있다.

Karush-Kuhn-Tucker (KKT) conditions
이제 이 maximum margin solution 를 해결하기 위해 KKT condition 과 lagrangian 을 도입한다.
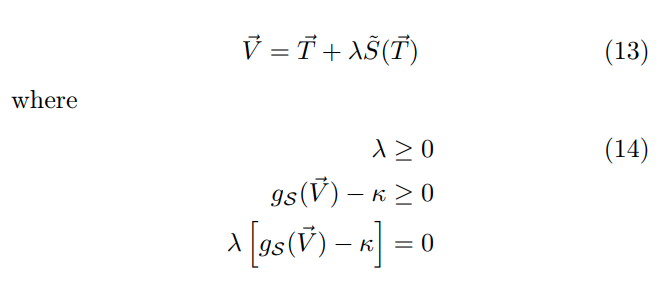
이 때 저 는 subgradient of the support function at 이다. minimal overlap 을 가지면서 S 의 convex hull 에 위치하는 point 이다. support function 이 differentiable 한 경우에는subgradient 가 unique 하게 결정되는데, 우리의 경우 g 가 not differentiable 한 경우에, 그 subgradient 자체가 conv(S) 자체에 들어가 있지 않기 때문에, convex hull 이용해 optimization 했을 때 lambda 는 self consistent equation 을 가진다.

Mean field interpretation of the KKT relations
KKT relations 는 mean field theory framework 에서 큰 기여를 한다. 우선 lambda 를 위에서 정의 했기 때문에 one per manifold 에 대해서 solution 은 다음과 같이 쓰여진다.

이를 square 하면 아래와 같이 계산이 되고,

correlation 을 무시했을 때 아래와 같은 KKT expression for the capacity 를 얻게 된다.
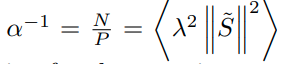
mean field theory 를 통해 self-consistent equation of the fields 로부터 "single" manifold 상의 적절한 statistics 를 유도할 수 있다. 이를 확인하기 위해, 저자는 solution vector w 를 하나의 manifold 위에 projection 시켰고, 이로부터 유도한 w 식이 결국 최적화 문제의 시작 (equation 13) 과 닮아 있음을 확인함으로써, equation 13 이 just the decomposition of the field induced on a specific manifold into the contribution induced by that specific manifold 이라는 것을 관찰한다.
Anchor points and manifold supports
vectors 들을 라고 denote 하고 "manifold anchor points" 라고 새롭게 정의한다. 특정 manfold configuration 에서 manifold 들은 set of P anchor point 로 되어도 같은 maximum margin solution 을 내뱉는다. 하지만 individual anchor point 는 manifold configuration 에 의해서도 결정되지만, random orientations of all the other manifolds 에 의해서도 결정된다. fixed manifold 가 있을 때 location of anchor point 는 다른 manifold 위치에 따라 달라지는데, 이 variation 은 mean field theory 에서 dependence of the anchor point on the random Gausian vector 에 의해 설명될 수 있다.
특히, 이 anchor point location in convex hull 은 manifold 와 margin planes 간의 관계를 설명한다. 일반적으로 일부 manifold 는 margin hyperplanes 와 intersection 이 있는데 얘네는 support manifolds of the system 이다. 이 "touching manifold" 의 variation 은 dimension of the span of the intersecting set of conv (S) with the margin planes "k" 에 의해 설명된다. intersect 가 일어나는 곳은 manifold 의 anchor point 이며, k=1 일 때 특히 boundary of S 에서 만나게 된다. 반대로 K=D+1 일 때 fully supporting manifolds 는 completely reside in the margin hyperplane 하는 성질을 갖게 된다. 이 경우 S 의 translation vector c 와 V 는 parallel 관계이고, S 안의 모든 point 는 support vector 이며 V 와 kappa 라는 same overlap 을 가지게 된다. 또한 interior point of conv(S) 의 unique point 만이 equation 13 (self-consistent equation) 을 따르게 된다.
Conic decomposition
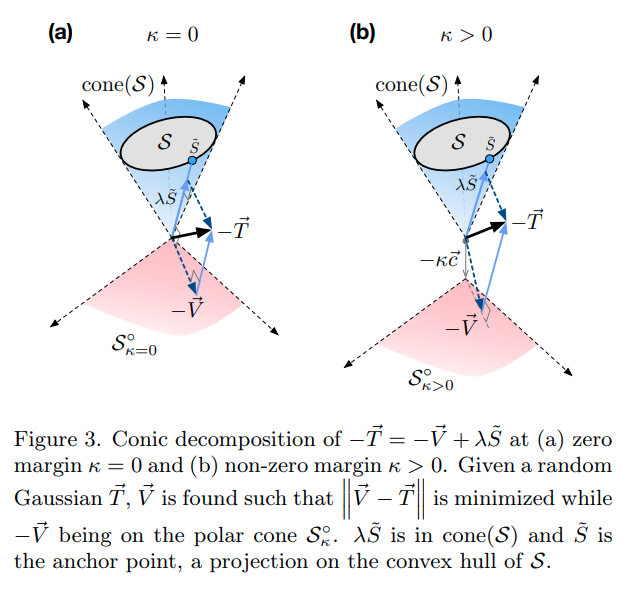
KKT conditions 는 conic decomposition of 관점에서도 해석할 수 있다. 이는 Euclidean projection 을 통해 해당 벡터를 linear subspaces 와 their null space 로 분해할 수 있다. 마찬가지로 fully suporting manifold 의 경우 는 cone(S) 내부에 위치하게 되고, 관계를 만족한다.
Numerical solution of the mean field equations
먼저 mean field equation 을 푸는 과정은 두 stage 로 나뉜다. 첫 번째 단계에서는, 주어진 에 대해 와 를 결정하기 위해, qudratic semi-infinite programming (QSIP) 문제를 해결한다. 특히, l2 ellipsoids 와 같은 간단한 기하학적 구조 상에서 analytically solve 가 가능하고, 이는 무한히 많은 점을 포함할 수 있는 manifold S에 대해 수행되는데, QSIP 문제를 효율적으로 해결하기 위해 cutting edge method 방법이 새롭게 고안되었다. 두번째로 Gaussian in D+1 dimension 에서 sampling 하고 mean field methods 에서 했던 것 처럼 average 하여 expectation, 즉 inverse capacity 를 계산한다.
work in progress...
