
📕 범위를 반씩 좁혀가는 탐색
📜 순차탐색
리스트 안에 있는 특정한 데이터를 찾기 위해 앞에서부터 데이터를 하나씩 차례대로 확인하는 방법이다.
- 따라서 데이터의 개수가 N개면 최악의 경우 시간복잡도 O(n)을 가지게 된다.
import java.util.*;
public class Main {
// 순차 탐색 소스코드 구현
public static int sequantialSearch(int n, String target, String[] arr) {
// 각 원소를 하나씩 확인하며
for (int i = 0; i < n; i++) {
System.out.println(arr[i]);
// 현재의 원소가 찾고자 하는 원소와 동일한 경우
if (arr[i].equals(target)) {
return i + 1; // 현재의 위치 반환 (인덱스는 0부터 시작하므로 1 더하기)
}
}
return -1; // 원소를 찾지 못한 경우 -1 반환
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
System.out.println("생성할 원소 개수를 입력한 다음 한 칸 띄고 찾을 문자열을 입력하세요.");
// 원소의 개수
int n = sc.nextInt();
// 찾고자 하는 문자열
String target = sc.next();
System.out.println("앞서 적은 원소 개수만큼 문자열을 입력하세요. 구분은 띄어쓰기 한 칸으로 합니다.");
String[] arr = new String[n];
for (int i = 0; i < n; i++) {
arr[i] = sc.next();
}
// 순차 탐색 수행 결과 출력
System.out.println(sequantialSearch(n, target, arr));
}
}📜 이진탐색 : 반으로 쪼개면서 탐색하기
배열 내부의 데이터가 정렬되어 있어야 사용할 수 있는 알고리즘입니다. 찾으려는 데이터와 중간점 위치에 있는 데이터를 반복적으로 비교해서 원하는 데이터를 찾습니다.
- 위치를 나타내는 변수 3개를 가지고 있습니다.
- 시작점
- 중간점(소수점 이하는 버립니다.)
- 끝점
- 1번 확인할 때마다 절반이 사라지기 때문에 시간복잡도 O(logN)을 가지게 됩니다.
- 이진 탐색을 구현하는 방법에는 2가지가 있습니다.
- 재귀 함수
- 반복문
- 탐색 범위가 2000만을 넘어가면 이진탐색으로 접근합니다.
- 보통 처리할 데이터 양이 1000만 단위 이상이 되면 이진탐색과 같은 O(logN)방법으로 해결해야 합니다.
🔔 재귀 함수 방식
import java.util.*;
public class Main {
// 이진 탐색 소스코드 구현(재귀 함수)
public static int binarySearch(int[] arr, int target, int start, int end) {
if (start > end) return -1;
int mid = (start + end) / 2;
// 찾은 경우 중간점 인덱스 반환
if (arr[mid] == target) return mid;
// 중간점의 값보다 찾고자 하는 값이 작은 경우 왼쪽 확인
else if (arr[mid] > target) return binarySearch(arr, target, start, mid - 1);
// 중간점의 값보다 찾고자 하는 값이 큰 경우 오른쪽 확인
else return binarySearch(arr, target, mid + 1, end);
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// 원소의 개수(n)와 찾고자 하는 값(target)을 입력받기
int n = sc.nextInt();
int target = sc.nextInt();
// 전체 원소 입력받기
int[] arr = new int[n];
for (int i = 0; i < n; i++) {
arr[i] = sc.nextInt();
}
// 이진 탐색 수행 결과 출력
int result = binarySearch(arr, target, 0, n - 1);
if (result == -1) {
System.out.println("원소가 존재하지 않습니다.");
}
else {
System.out.println(result + 1);
}
}
}🔔 반복문
import java.util.*;
public class Main {
// 이진 탐색 소스코드 구현(반복문)
public static int binarySearch(int[] arr, int target, int start, int end) {
while (start <= end) {
int mid = (start + end) / 2;
// 찾은 경우 중간점 인덱스 반환
if (arr[mid] == target) return mid;
// 중간점의 값보다 찾고자 하는 값이 작은 경우 왼쪽 확인
else if (arr[mid] > target) end = mid - 1;
// 중간점의 값보다 찾고자 하는 값이 큰 경우 오른쪽 확인
else start = mid + 1;
}
return -1;
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// 원소의 개수(n)와 찾고자 하는 값(target)을 입력받기
int n = sc.nextInt();
int target = sc.nextInt();
// 전체 원소 입력받기
int[] arr = new int[n];
for (int i = 0; i < n; i++) {
arr[i] = sc.nextInt();
}
// 이진 탐색 수행 결과 출력
int result = binarySearch(arr, target, 0, n - 1);
if (result == -1) {
System.out.println("원소가 존재하지 않습니다.");
}
else {
System.out.println(result + 1);
}
}
}
🔔 파라메트릭 서치
최적화 문제를 결정 문제로 바꾸어 해결하는 기법이다. '원하는 조건을 만족하는 가장 알맞는 값을 찾는 문제'에 주로 사용이 된다.
- 이진탐색을 이용하면 된다.
- 떡복이 떡 만들기 문제
📜 트리 자료구조
DB에서 트리 자료구조를 이용해서 항상 데이터가 정렬이 되어있습니다. 이진탐색과 비슷한 방법을 이용해서 탐색을 매우 빠르게 합니다.
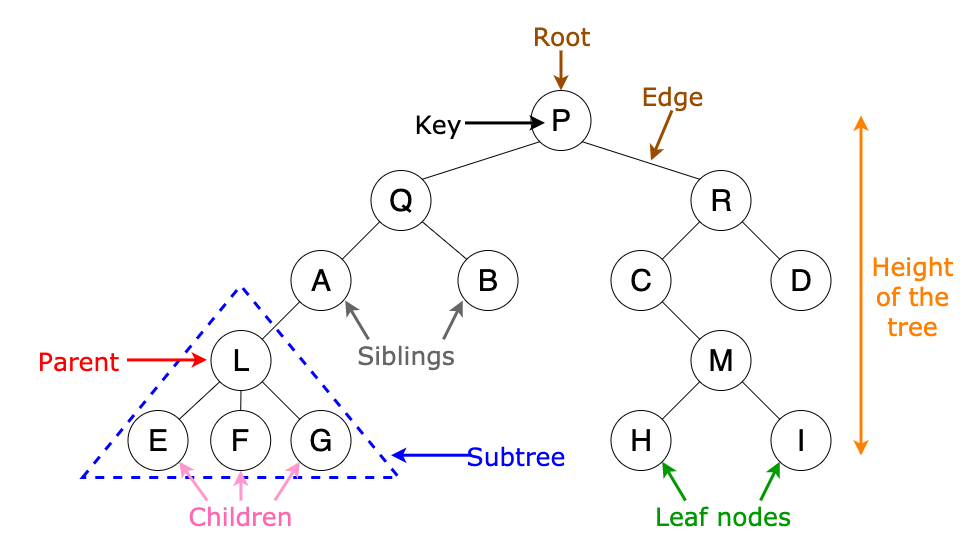
- 노드와 노드의 연결로 표현하며 여기에서 노드는 정보의 단위로서 어떠한 정보를 가지고 있는 개체로 이해할 수 있습니다.
- 그래프에서의 노드와 동일합니다.
🔔 트리 자료구조 특징
- 트리는 부모노드와 자식노드의 관계로 표현된다.
- 트리의 최상단 노드를 루트노드라고 한다.
- 트리의 최하단 노드를 단말노드라고 한다.
- 트리에서 일부를 떼어내도 트리 구조이며 이를 서브 트리라고 한다.
- 트레는 파일 세스템과 같이 계층적이고 정렬된 데이터를 다루기에 적합하다.
📜 이진 탐색 트리
이진 탐색이 동작할 수 있도록 고안된, 효율적인 탐색이 가능한 알고리즘입니다.
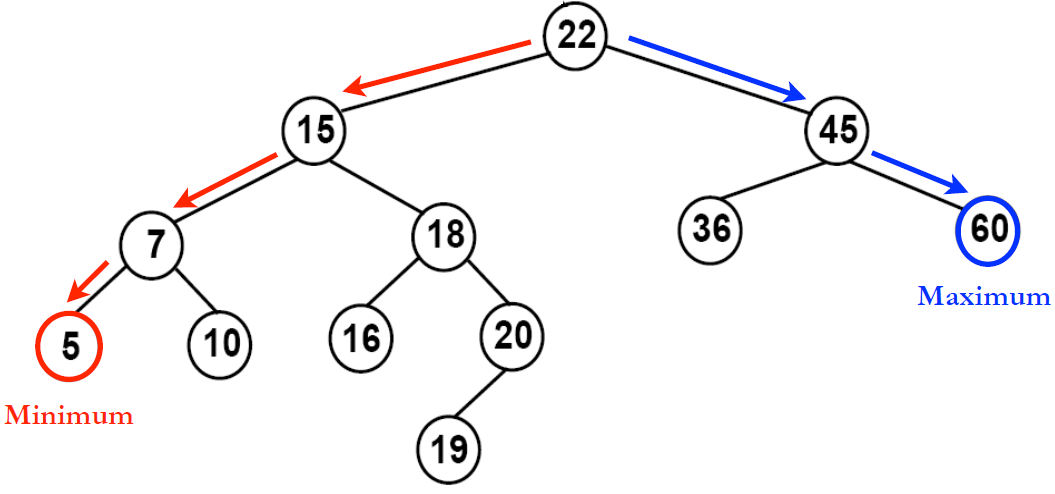
🔔 이진 탐색 트리 특징
- 부모 노드보다 왼쪽 자식 노드가 작다.
- 부모 노드보다 오른쪽 자식 노드가 크다.
- 왼쪽 자식 노드 < 부모 노드 < 오른쪽 자식 노드
참조
https://hanamon.kr/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-tree-%ED%8A%B8%EB%A6%AC/
.
https://ratsgo.github.io/data%20structure&algorithm/2017/10/22/bst/
