🎈 문제 풀이

• 상대적으로 고난도 문제이므로 이 문항에 대한 답안을 내지 못했다고 해서 지나치게 아쉬워하지 않아도 괜찮습니다. 이 문항에서 사용되는 자료구조/알고리즘 (아이디어) 학습에 중점을 두어 읽어주시기 바랍니다.
• Lv.3 문항은 충분한 학습의 시간을 가진 뒤에 다시 복습하는 것도 좋습니다.

풀이1 - 트리를 이용한 풀이

문제 단순화하기

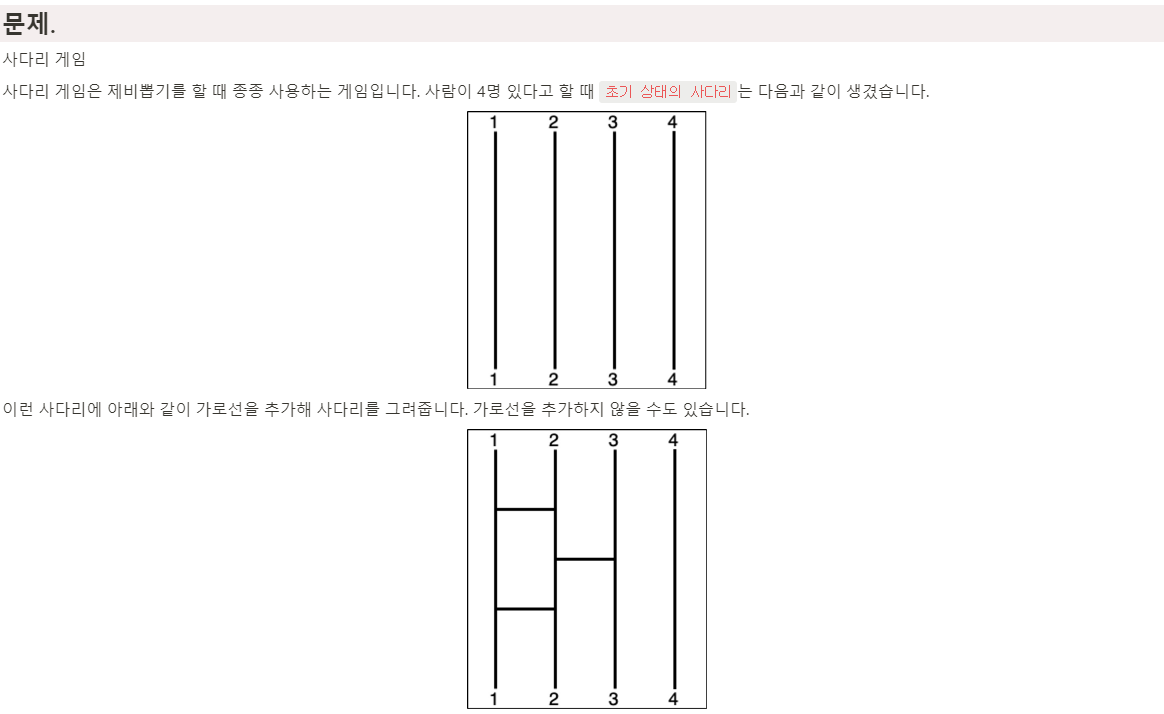
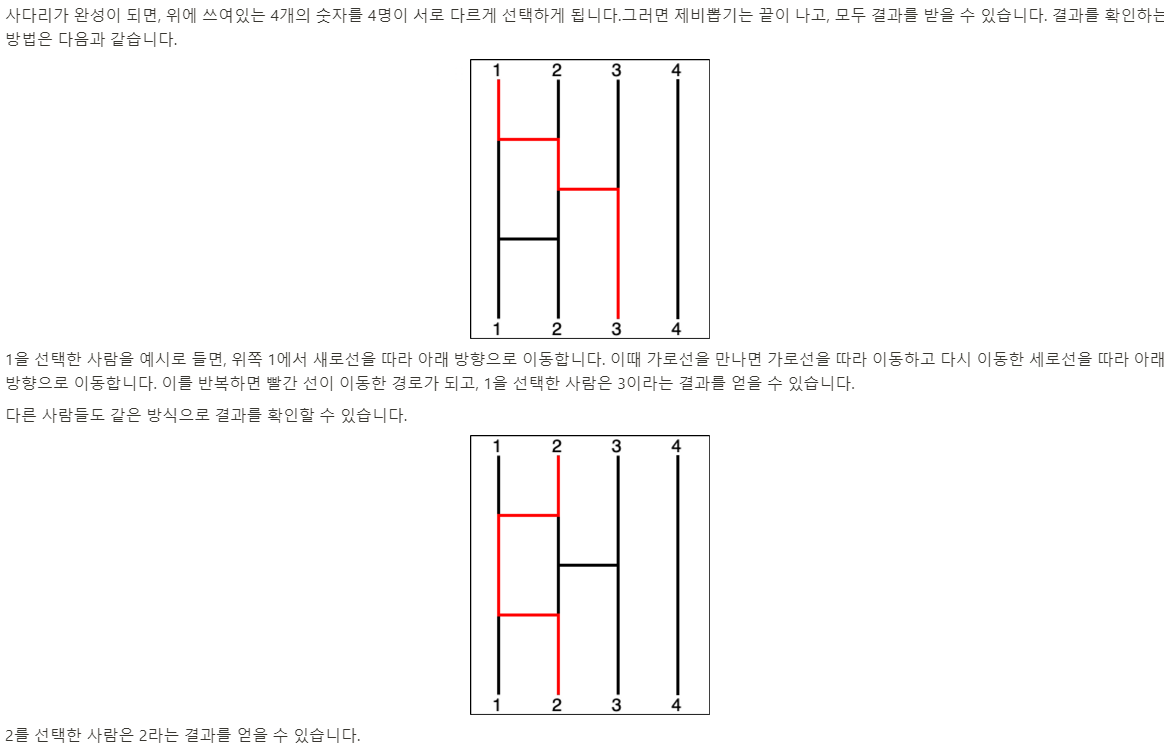
이러한 류의 문제는 문제를 있는 그대로 받아들이기 전에, 우선 문제를 단순화시킬 수 있는지 생각해보아야 합니다. 사다리 게임에서 사다리에 가로선을 추가하는 것은 어떤 의미를 가지는지 생각해보겠습니다. 가로선을 추가하면 그 가로선이 연결 하는 두 숫자의 흐름은 서로 바뀌게 되는데 이는 결과적으로 두 숫자를 바꾸는(Swap) 효과와 같습니다.

추가로, 가로선은 항상 서 로 인접한 세로선 사이에만 추가할 수 있기 때문에 사다리 게임에서 가로선을 추가하는 행동은 인접한 두 숫자를 바꾸는 것과 동치 입니다.

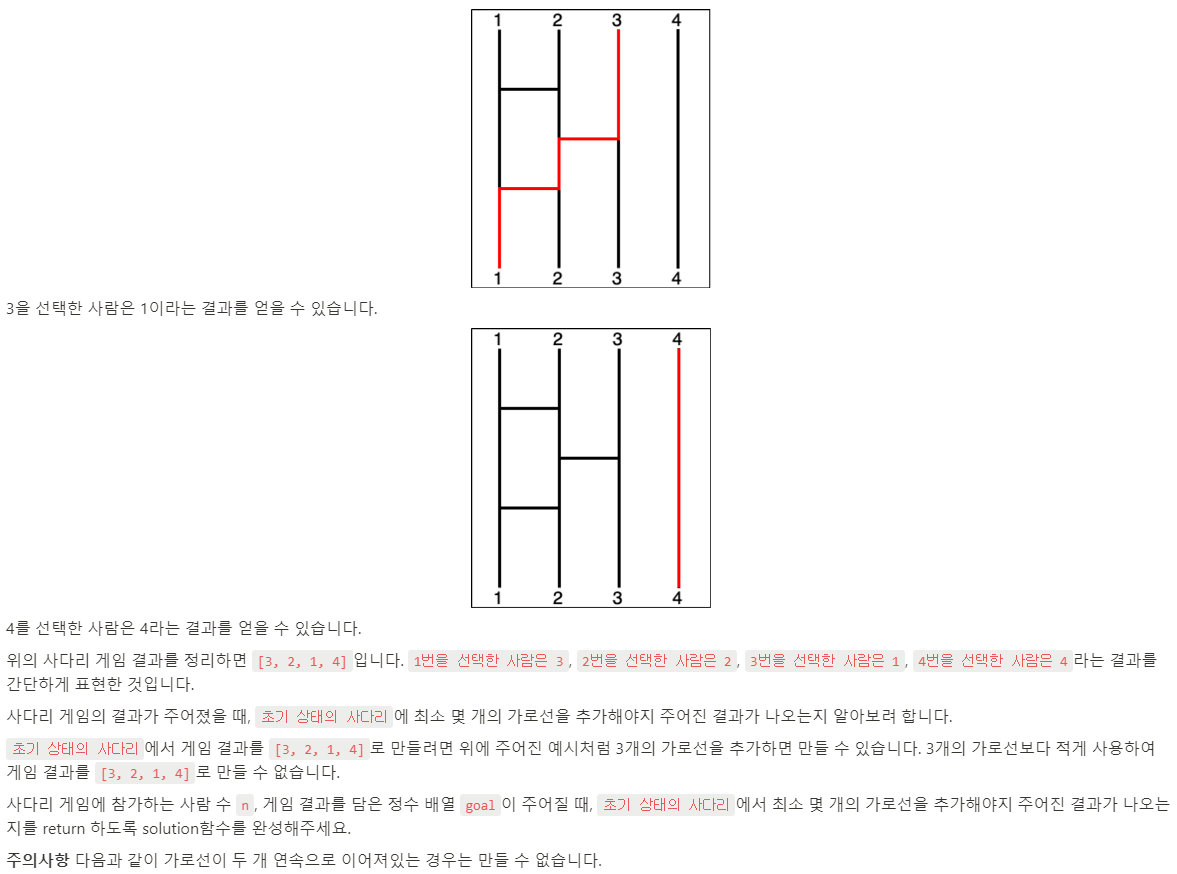
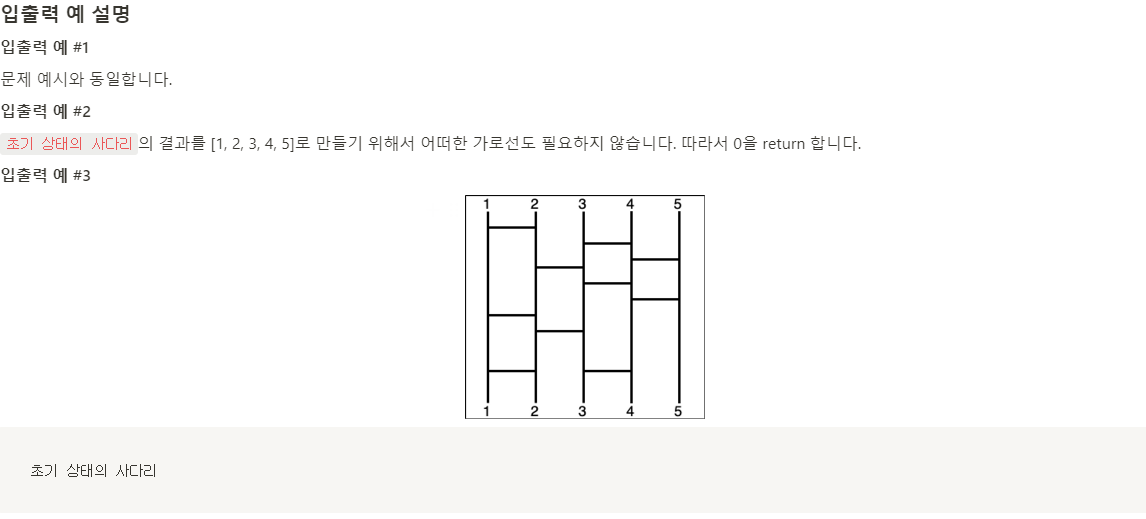
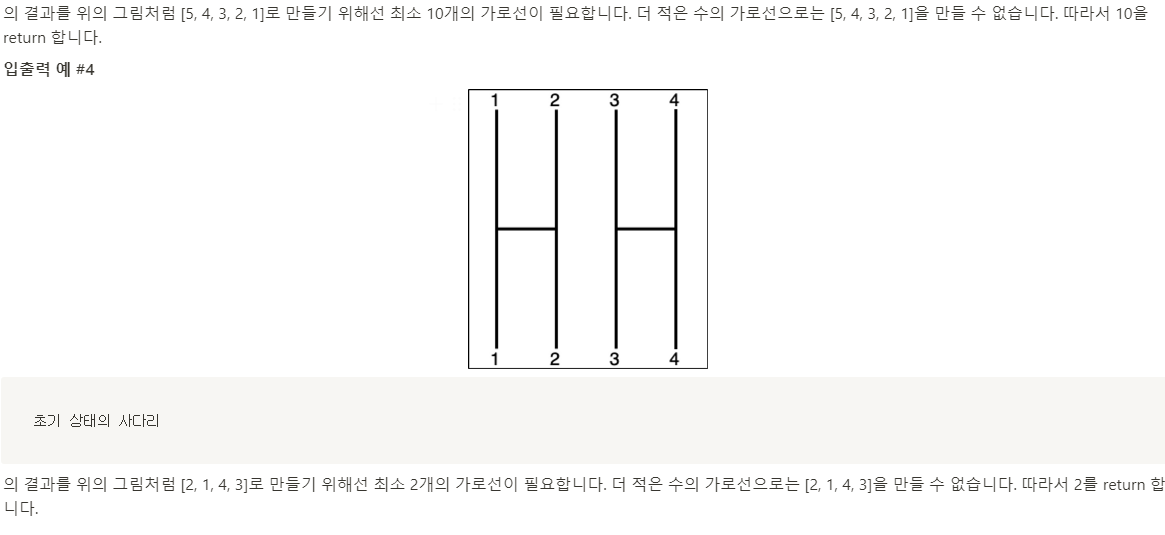
예를 들어, 입출력 첫번째 예시로 주어진 [3, 2, 1, 4] 는 그림에서 볼 수 있듯 1-2 사이 가로선, 2-3 사이 가로선, 1-2 사이 가 로선이 순서대로 배치되어있는 사다리의 결과 리스트입니다. 이는 [1, 2, 3, 4] 배열에서 첫번째와 두번째, 두번째와 세번째, 첫번째와 두번째 원소를 Swap한 뒤의 결과와 같습니다.

이를 통해 우리가 알 수 있는 가장 큰 힌트는, 문제 상황이 아래와 같이 단순화될 수 있다는 것입니다.

길이가 n인 배열이 주어진다. 인접한 두 원소의 값을 바꾸는 연산을 최소한으로 적용하여 배열을 정렬된 상태로 만들고 싶다. 필요한 연산의 최소 횟수는 얼마인가?

이와 같이 정렬을 하는데 필요한 Swap의 최소 횟수를 묻는 문제는 이미 잘 알려져있습니다.[1][2][3]

그리고 이러한 문제 상황에 서 필요한 Swap의 최소 횟수는 배열에 존재하는 Inversion의 개수와 같습니다.

여기서 Inversion이란, 정렬 순서를 위배하는 한 쌍의 원소를 말합니다.

(이를 조금 더 엄밀히 설명하면 배열의 두 인덱스 $i$, $j$ 에 대하여 $i < j$이고 $a_i > a_j$이면 이 $(i, j)$를 Inversion이라고 부릅니다. 코딩 테스트 해설 등에서 종종 등장하는 용어이니 알아두는 것이 좋습니다.)

필요한 Swap의 횟수가 Inversion의 수와 같다는 것을 수학적으로 엄밀하게 증명할 수도 있겠지만

여기서는 조금 직관적으로 논해봅시다. (좀 더 엄밀한 증명은 외부에서 쉽게 찾을 수 있습니다.[4])
배열과 Inversion의 수에는 아래와 같은 성질이 성립합니다.

• 이미 정렬된 배열에는 Inversion의 수가 0이다.
• 배열에서 인접한 Swap을 한번 수행하면 Inversion을 최대 1만큼 줄일 수 있다.
• Inversion이 존재하는 배열이라면 인접한 Swap을 통해 Inversion이 감소하는 위치가 무조건 존재한다.

위 세가지 성질을 생각하면, Swap을 여러번 수행하면서 Inversion 개수를 1씩 줄여나가다보면 언젠가 Inversion이 없는, 정렬 된 상태의 배열을 얻을 수 있고, 필요한 Swap의 횟수는 Inversion의 개수와 같다는 것을 도출할 수 있습니다.

이렇게 되면 문제는 더욱 간단해집니다.

길이가 인 배열에 존재하는 Inversion의 수를 구하여라.

Inversion의 개수 구하기

그럼 Inversion의 개수를 구해봅시다. 배열에서 Inversion의 개수를 세려면,
배열을 첫 원소부터 끝까지 순회하면서, 현재 $i$번째 원소를 보고 있다면 $[0, i - 1]$에 속하는 원소들 중 $a_i$보다 큰 원소의 개수를 세고 이를 정답 변수에 합해주는 것을 반복하면 됩니다.
이전 위치에서 현재 값보다 큰 원소의 개수를 세는 것이 결국 정렬 순서를 위배하는 쌍의 개수를 구하는 것과 같기 때문입니다.

이를 구현하는데 세그먼트 트리(Segment Tree)[5]나 펜윅 트리(Fenwick Tree)[6]와 같이

구간 합을 빠르게 구하고 특정 위치의 값을 업데이트하는 것을 지원하는 자료구조(특별한 형태의 트리)를 이용할 수 있습니다. 이 두 자료구조는 최근 코딩 테스트에서 고난이도 문제에 등장하는 자료구조입니다.

세그먼트 트리와 펜윅 트리는 모두 특별한 형태의 트리입니다. 
코딩테스트/알고리즘 대회에서 트리를 활용할 때에는 내장 라이브러리를 사용하는 경우와 
직접 트리를 정의하여 사용하는 경우로 나뉘는데, 
세그먼트 트리와 펜윅 트리는 모두 후자(직접 트리를 정의하여 사용하는 경우)에 속한다고 볼 수 있습니다.
이진 트리를 직접 정의하여 활용하는 것에 익숙하다면 위 두 트리를 이해하는 것도 어렵지 않을 것입니다.

배열에 존재하는 원소의 최댓값이 $n$이므로 1부터 $n$까지의 구간을 표현할 수 있는 트리를 만드는 것으로 시작합니다.

현재 $i$번째 원소를 보고 있다면 트리를 통해 값이 $[a_i + 1, n]$에 속하는 개수를 세고
이를 정답 변수에 합해준 뒤, 트리의 $a_i$위치에 1을 더해 주면 됩니다.

둘 중 어느 자료구조를 사용해도 Inversion을 구하는데 활용할 수 있기 때문에 개인의 기호에 따라 선택해도 되지만, 펜윅 트리는 세그먼트 트리보다 구현이 훨씬 간단하기 때문에 시간이 한정되어있는 코딩 테스트에 안성맞춤입니다.

풀이2 - 병합 정렬을 이용한 풀이

이 문제는 다른 방향으로 문제를 바라볼 수 있습니다.

사다리 타기의 가로선에 대해서 다시 생각해봅시다.

가로선이 생기면 인접한 두 라인이 서로 가로선에 의해 바뀌게 됩니다.

예를 들어, 1번 라인과 2번 라인에 가로선을 그리면 1번 라인은 2번으로, 2번 라인은 1번으로 가게 됩니다.

즉, 가로선을 그리는 행위는 라인을 SWAP 하는 것과 동일한다는 것을 알 수 있습니다.

문제의 요구 사항에 대해 생각해봅시다. 우리는 최소한의 가로선을 이용해서 [1, 2, 3, …, N] 인 사다리를
주어진 Goal 상태로 결과가 나오도록 변경해야됩니다. 반대로 생각하면 우리는 Goal 상태를 [1, 2, 3, …, N]
으로 바꾼다고 생각해도 됩니다.

위의 두 가지 사실을 통해, 우리는 주어진 Goal 배열을 [1, 2, 3, …, N] 상태로 만드는데 최소 몇번의
SWAP이 필요한지로 문제를 다르게 해석 할 수 있습니다.

이제 여기에 Merge Sort(합병정렬) 알고리즘을 도입해보겠습니다.

주어진 Goal 배열을 [1, 2, 3, …, N] 으로 만든다는 것을 오름차순으로 정렬하는 것과 동일합니다.

즉, Merge Sort 과정에서 몇 번의 SWAP 이 일어나는지 알 수 있다면 문제를 해결 할 수 있습니다.

Merge Sort 는 크게 Divide and Conquer 부분과 Merge 과정으로 나누어 생각 할 수 있는데,

Merge 과정에서 우측에 있는 숫자들이 왼쪽에 있는 숫자보다 작다면 재배치가 일어나게 되고 이때 SWAP이 발생하게 됩니다.

주어진 Goal 을 Merge Sort 로 정렬하면서 SWAP 이 몇 번 일어났는지 Count 하면 문제를 해결 할 수 있습니다.

import java.util.Arrays;

public class Solution {
    int[] arr; // 분할 정복을 위해 선언한 전역배열, goal 값으로 세팅해준다.
    int[] tmp; // 분할 정복을 위한 임시배열
    long answer;

    public long solution(int n, int[] goal) {
        arr = Arrays.copyOf(goal, n);
        tmp = new int[n];

        answer = 0;

        mergeSort(0, n - 1);

        return answer;
    }

    /**
     *  분할 정복을 이용한 Merge Sort 를 진행한다.
     */
    void mergeSort(int start, int end) {
        if (start >= end) { // 끝까지 분할 한 경우
            return;
        }

        int mid = (start + end) / 2;
        mergeSort(start, mid);
        mergeSort(mid + 1, end);
        merge(start, end);
    }

    /**
     *  분할 List를 Merge 한다.
     */
    void merge(int left, int right) {
        int mid = (left + right) / 2;
        int leftIdx = left;     // 좌측 배열 탐색 인덱스
        int rightIdx = mid + 1;   // 우측 배열 탐색 인덱스
        int tempIdx = left;     // 임시 저장 배열 인덱스

        while (leftIdx <= mid && rightIdx <= right) {
            if (arr[leftIdx] <= arr[rightIdx]) {
                tmp[tempIdx++] = arr[leftIdx++];
            } else {
                tmp[tempIdx++] = arr[rightIdx++];
                answer += (mid - leftIdx + 1); // !몇 번의 SWAP을 통해 Merge 할 수 있는지 Count 합니다.!
            }
        }

        while (leftIdx <= mid) {
            tmp[tempIdx++] = arr[leftIdx++];
        }

        while (rightIdx <= right) {
            tmp[tempIdx++] = arr[rightIdx++];
        }

        for(int i = left; i <= right; i++) {
            arr[i] = tmp[i];
        }
    }

}

[1][https://www.geeksforgeeks.org/number-swaps-sort-adjacent-swapping-allowed/](https://www.geeksforgeeks.org/number-swaps-sort-adjacent-swapping-allowed/)

[2][https://stackoverflow.com/questions/20990127/sorting-a-sequence-by-swapping-adjacent-elements-using-minimum-swaps](https://stackoverflow.com/questions/20990127/sorting-a-sequence-by-swapping-adjacent-elements-using-minimum-swaps)

[3][https://www.acmicpc.net/problem/10090](https://www.acmicpc.net/problem/10090)

[4][https://stackoverflow.com/questions/20990127/sorting-a-sequence-by-swapping-adjacent-elements-using-minimum-swaps](https://stackoverflow.com/questions/20990127/sorting-a-sequence-by-swapping-adjacent-elements-using-minimum-swaps)

[5][https://codingnojam.tistory.com/49](https://codingnojam.tistory.com/49)

[6][https://loosie.tistory.com/647](https://loosie.tistory.com/647)

import java.util.Arrays;

public class Solution {
    public long solution(int n, int[] goal) {
        // 해설에서 설명한 것 처럼, 필요한 가로선의 수는
        // 결론적으로 배열에 존재하는 Inversion의 개수에 비례함.
        // Inversion의 개수를 저장하는 answer 변수와
        // 각 숫자의 개수를 저장하고 업데이트하는 것을 효율적으로 수행하는
        // FenwickTree(또는 Segment Tree도 가능)를 초기화.
        long answer = 0;
        FenwickTree count = new FenwickTree(n+1);
        for (int i = 0; i < n; ++i) {
            count.update(goal[i], 1);
            // 이전에 본 숫자들 중 goal[i]+1 이상 n 이하인 원소는
            // 정렬 순서를 위배하는, 즉 Inversion에 해당하는 원소임.
            answer += count.query(goal[i]+1, n);
        }
        return answer;
    }
}

// 같은 일을 하는 Segment Tree로 대체 가능.
// 그러나, Segment Tree보다 Fenwick Tree가 훨씬
// 간단하기 때문에, 시간내에 구현하기 쉬움.
class FenwickTree {
    private long[] tree;
    
    public long query(int end) {
        long result = 0;
        while (end > 0) {
            result += tree[end];
            end -= (end & -end);
        }
        return result;
    }

    public void update(int pos, long add) {
        while (pos < tree.length) {
            tree[pos] += add;
            pos += (pos & -pos);
        }
    }

    public long query(int start, int end) {
        return query(end) - query(start-1);
    }

    public FenwickTree(int count) {
        tree = new long[count];
        Arrays.fill(tree, 0);
    }
}