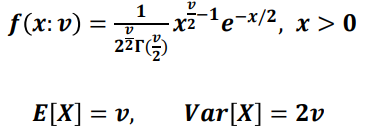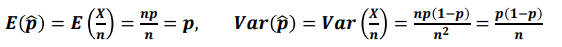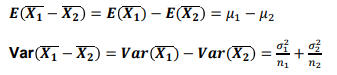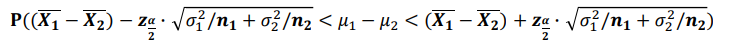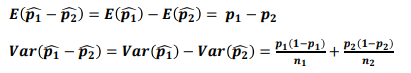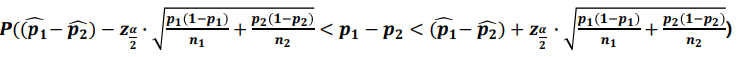통계 기초_2

YJ·2023년 5월 1일

통계

📖 05_모집단과 표본 분포

1) 모집단과 표본

2) 표본 분포

📖 06_추정

▷ 오늘 학습 계획: 통계 강의(기초 4~5)

📖 05_모집단과 표본 분포

1) 모집단과 표본

표본추출(Sampling): 모집단으로 부터 표본을 추출 하는 것
복원추출(Sampling with replacement)
비복원추출(Sampling without replacement)
Random Sampling

불균형 데이터(Imbalanced Data)의 문제
예측 대상이 전체 대비 아주 낮다면 Sampling 기법(Over Sampling, Under sampling) 또는 모델을 통한 성능 개선
Over Sampling → 과도적합의 문제
Under sampling → 데이터가 편향 될 수 있음, 모형의 성능이 떨어질 수 있음

2) 표본 분포

통계량(Statistic): 표본에 기초하여 계산되는 수치 함수
표본분포(Sampling distribution): 통계량들이 이루는 분포

중심극한 정리

카이제곱 분포(Chi-square distribution)

자유도(degree of freedom): 일반적으로 n-1을 사용함
자유도 v의 크기에 따라 모양이 달라짐(자유도가 커질수록 좌우 대칭)
자유도가 커지면서 표준정규 분포에 근사하며 v>=30이면 확률을 근사적으로 정규분포로 구할 수 있음

T분포(t-distribution)

F분포(F distribution)

서로 독립인 두 정규모집단의 분산 또는 표준편차들의 비율에 대한 통계적 추론, 분산분석 등에 활용

📖 06_추정

1) 추정

추정(estimation): 모집단의 모수를 모를 경우 표본으로 추출된 통계량을 모집단의 근사값으로 사용하는 것
추정량(estimator): 표본 평균으로 모평균을 추정할 때 표본 평균을 모평균에 대한 추정량이라고 함

점추정: 모수를 하나의 특정값으로 추정

일치성(Consistency): 표본의 크기가 모집단의 크기에 근접
불편성(unbiased estimator): 추정량이 모수와 같아야 함
유효성(efficiency): 추정량의 분산이 최소값이어야 함
평균오차제곱(Mean Squared Error, MSE)이 최소

구간 추정: 모수가 포함될 수 있는 구간을 추정

신뢰구간(confidence level): 추정값이 존재하는 구간에 모수가 포함될 확률
100*(1-a)%로 계산 하며, a는 오차 수준
오차 = 유의수준(significant level)

모평균의 구간추정

모집단의 분산을 아는 경우

모집단의 분산을 모르는 경우 → t분포

허용오차(permissible error)
추정한 값이 틀려도 허용할 수 있는 오차 → 표본의 크기 결정

2) 모비율 추정

모비율의 점추정

모비율의 점추정량을 표본 비율(sample proportion)이라고 함

모비율의 구간 추정

모비율 구간 추정에서 정규분포의 근사가 가능한 대표본은
보통 np>5, n(1-p)>5 를 동시에 만족

모평균 차이의 추정(점추정)

모평균 차이의 추정(구간추정: 대표본)

모평균 차이의 추정(구간추정: 소표본, 모분산을 모를 때) → 등분산 가정

모비율 차이의 추정(점추정)

모비율 차이의 추정(구간추정)