문제
N명의 사람이 있고, 여기서 세 사람 A, B, C를 고르려고 한다. 세 사람은 모두 친구여야 한다.
세 사람을 고르는 방법은 매우 많이 있을 수 있다. 이때, A의 친구 수 + B의 친구 수 + C의 친구 수가 최소가 되어야 한다. 친구 수의 합을 계산할 때, 세 사람은 빼고 계산해야 한다. 즉, A의 친구 수를 계산할 때, B와 C는 빼고 계산해야 하고, B의 친구 수를 계산할 때는 A와 C, C의 친구 수를 계산할 때는 A와 B를 빼고 계산해야 한다.
입력
첫째 줄에 사람의 수 N(3 ≤ N ≤ 4,000), 친구 관계의 수 M(0 ≤ M ≤ 4,000)이 주어진다. 둘째 줄부터 M개의 줄에는 친구 관계를 의미하는 두 정수 A, B가 주어진다. 친구 관계는 A와 B, 그리고 B와 A가 친구라는 것을 의미한다.
사람은 1번부터 N번까지 번호가 매겨져 있다. 같은 친구 관계가 두 번 이상 주어지는 경우는 없다.
출력
첫째 줄에 A의 친구 수 + B의 친구 수 + C의 친구 수의 최솟값을 출력한다. 만약, 문제 조건대로 세 사람을 고를 수 없는 경우에는 -1을 출력한다.
풀이 및 회고
풀이
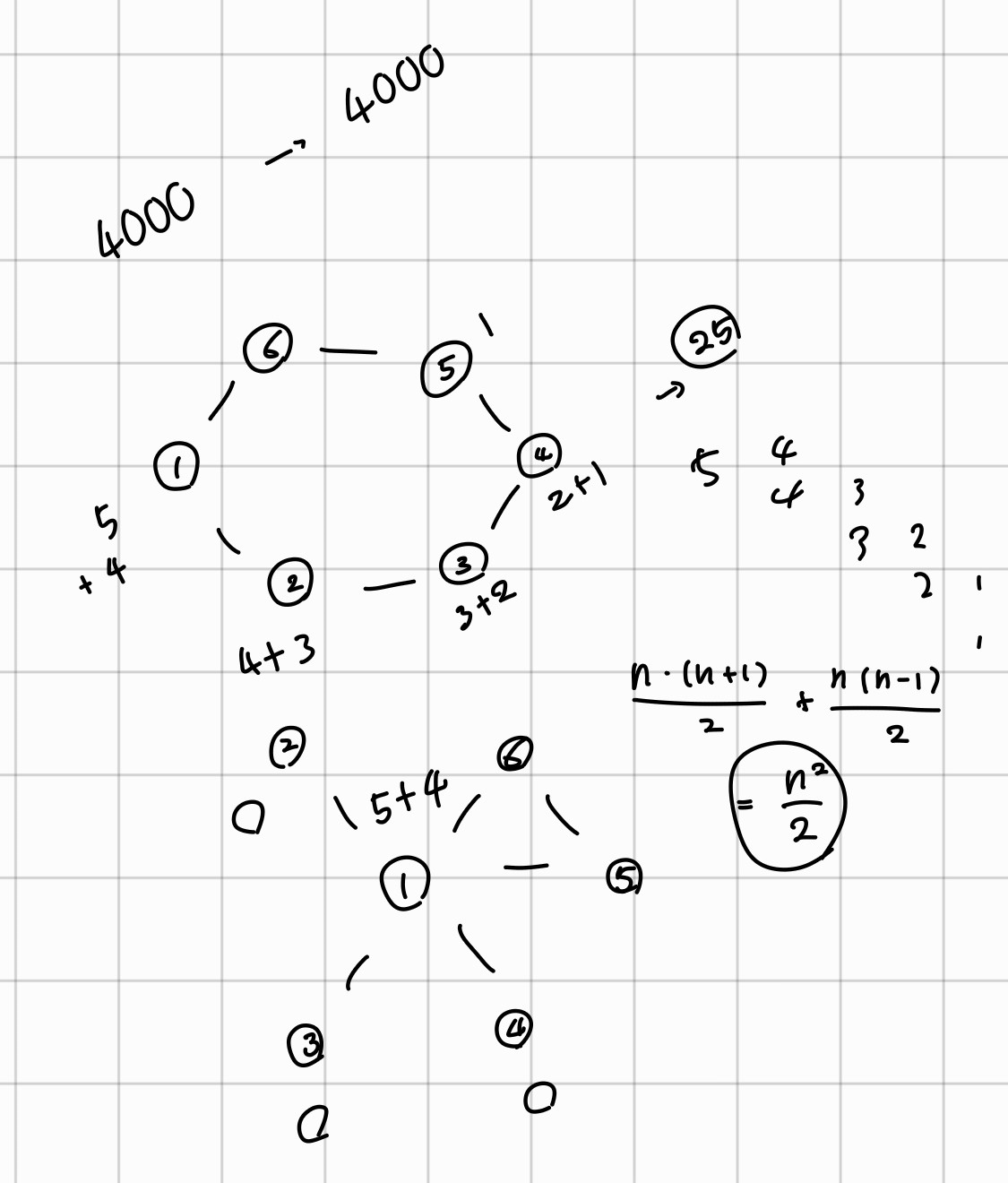
3중 반복문을 이용하여 모든 경우에 대해 탐색한다. 주어진 관계의 최댓값이 4000이므로 4000의 3제곱번 만큼의 계산은 이루어지지 않는다. 가장 최악의 경우는 모두가 관계를 가지는 사이클 형태의 그래프일 때 n**2 / 2의 시간복잡도를 가진다.(여러 케이스를 직접 계산해본 결과)
회고
처음에는 조합으로 여차저차 하려했지만 어림도없지 실패했다. 그래서 질문 게시판을 가봤더니 'n**3 같은데 왜 될까요?'라는 질문이 있길래 대충 증명해보고 맞췄다.. 증명에 꽤 시간을 써서 이게 해설을 한건지 내가 푼건지 헷갈리지만 뭐 어쨌든.. 증명한 그림이라도 첨부하겠다.
코드
n, m = map(int, input().split())
graph = [[0] * (n + 1) for _ in range(n + 1)]
friend_quantity = [0] * (n + 1)
for _ in range(m):
a, b = map(int, input().split())
graph[a][b] = 1
graph[b][a] = 1
friend_quantity[a] += 1
friend_quantity[b] += 1
minimum = 15000
for i in range(1, n - 1):
for j in range(i + 1, n):
if graph[i][j]:
for k in range(j + 1, n + 1):
if graph[i][k] == 1 and graph[j][k]:
minimum = min(
minimum,
friend_quantity[i]
+ friend_quantity[j]
+ friend_quantity[k]
- 6,
)
print(minimum if minimum < 15000 else -1)