서론

파이썬을 2.x버전(2.7)을 사용하거나 다른 언어들에서 소수를 사용하다보면 가끔 내가 저장했던 값과 다른 값이 저장되어 있는 모습을 볼 수 있다.

#include <stdio.h>

int main() {
    double pi = 3.14;
    double e = 2.71828;
    double y = 365.365;
    printf("%.20lf\n", pi);
    printf("%.20lf\n", e);
    printf("%.20lf\n", y);
    return 0;
}

C언어의 경우 위를 실행하면 각각 3.14000000000000012434.., 2.71828000000000002956..,
365.36500000000000909495..가 출력되는 것을 확인할 수 있다. 내가 저장했던 값과 다른 결과가 출력되는 것을 확인할 수 있는데 도대체 왜 이러한 문제가 생기는 걸까?

본론

소수를 저장하는 방식

소수를 저장하는 방식에는 두가지가 있다. 하나는 "고정소수점" 방식이고, 나머지 하나는 "부동소수점" 방식이다.

고정소수점 방식

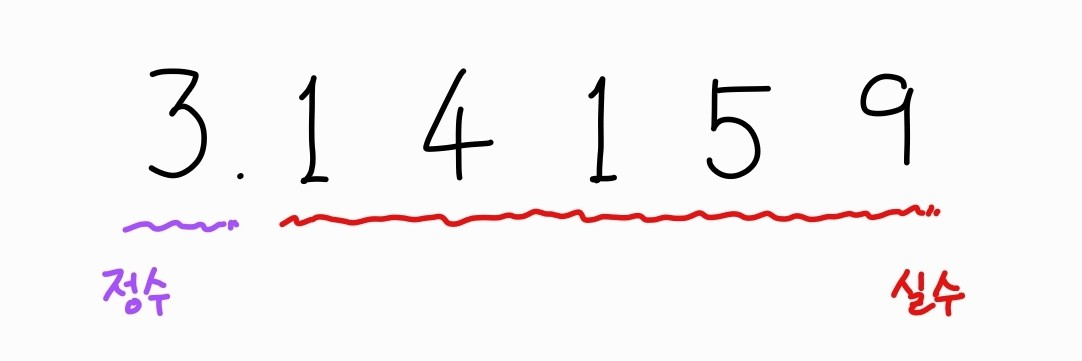
우리가 평소에 일상생활에서 사용하는 방식이 고정소수점 방식이다. 단순히 소수점을 기준으로 앞에는 정수부분을 기록하고 뒤에는 소수부분을 기록하는 방식이다. 무엇보다 보기 편하고, 소수점을 기준으로 표현해 비교적 단순하다는 장점이 있다.

고정소수점 방식으로 컴퓨터에 저장한다고 하면 부호, 정수부, 소수부로 총 3가지 요소가 필요하다. 첫 비트로 부호를 표현하고 미리 정해놓은 비트의 수로 정수부와 소수부를 표현한다.

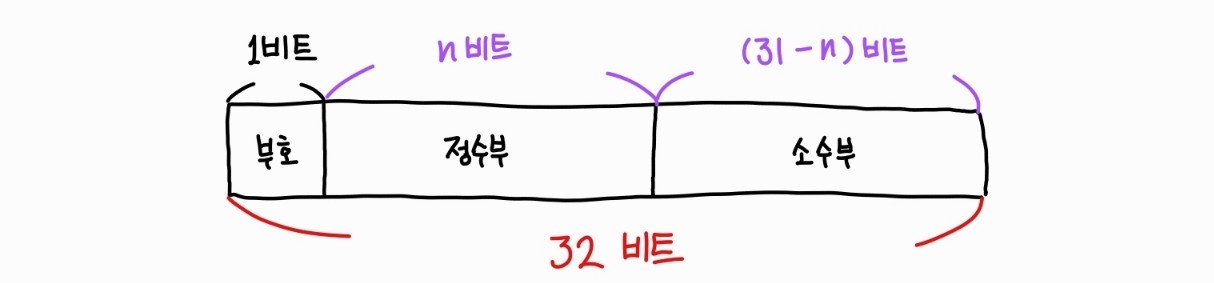
그러나 고정소수점 방식으로 컴퓨터에 저장할 경우에는 n의 값을 얼마로 설정해야하는지에 대한 딜레마가 생긴다. n의 값이 클 경우에는 큰 수를 표현하는 데에 있어서 장점을 보이지만 소수 부분의 값을 세밀하게 표현하지 못한다는 단점이 생긴다. 반면 n의 값이 작을 경우에는 소수 부분의 값을 세밀하게 표현한다는 장점이 있지만 큰 수를 표현할 수 없다는 단점이 생긴다.

이러한 딜레마를 해결하기 위해 컴퓨터에서는 부동소수점 방식을 채택하여 소수를 저장한다.

부동소수점 방식

부동소수점 방식은 소수를 표현하는 새로운 규칙을 제시한다.

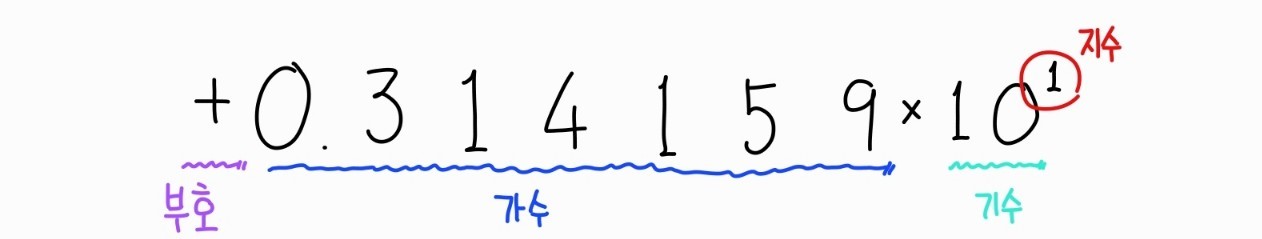
보통 계산기에서 지나치게 큰 값을 입력하면 '3.9e+30'와 같은 표현을 볼 수 있는데 이것이 바로 부동소수점 방식의 표현법이다! 위 표현은 '+3.9x10^30'을 의미한다.

이진수의 경우 다음과 같이 표현한다. '3.14159'를 예시로 들어보자. '3.14159'는 이진수로 '0011.00100100001..'(자세한건 소수를 이진수로 변환하는 법을 찾아보세요)이다. 위의 10진수와 별차이 없이 기수만을 2로 하여 '1.100100100001..x2^1'와 같이 표현하면 된다.

부동소수점 방식으로 컴퓨터에 저장할 때는 IEEE(Institute of Electrical and Electronics Engineers, 전지전자공학자협회)의 표준에 따라 표현에는 부호, 지수, 가수만을 사용한다.(기수는 당연히 2이므로 생략한다) 단정도 부동소수점(float: 32비트)은 부호 1비트, 지수 8비트, 가수 23비트로 구성하고, 배정도 부동소수점(double: 64비트)은 부호 1비트, 지수 11비트, 가수 52비트로 구성한다.(파이썬의 경우 배정도 부동소수점을 사용한다.) 위의 '3.14159'에 대한 예시로 알 수 있듯이 가수부분은 무한히 이어지는데, 가수부분은 미리 정해놓은 비트까지(23비트, 52비트)만을 사용하고 나머지 부분은 사용하지 않는다. 아래 그림은 단정도 부동소수점의 구성이다.

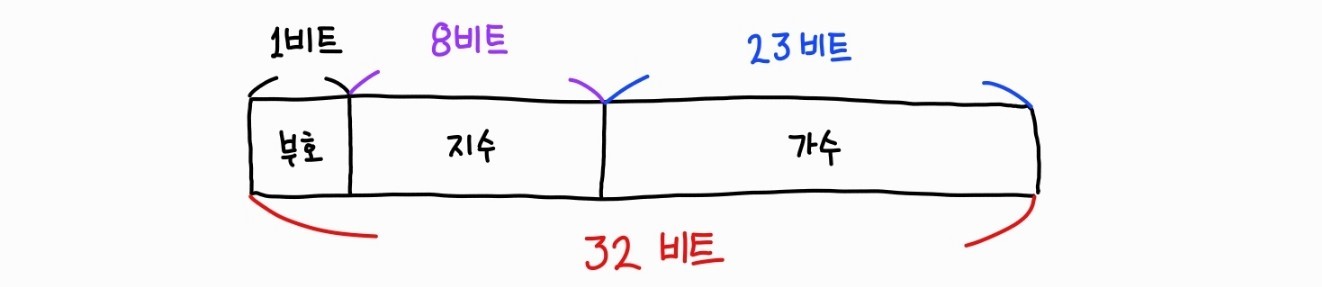
위에 예시로 든 '3.14159'('1.100100100001..x2^1')를 위의 그림에 끼워맞춰보자. 우선 부호의 경우 양수이므로 '1', 지수는 '1'이므로 '00000001', 가수는 맨 앞의 숫자는 항상 1이기 때문에 생략하여 '100100100001..'로 표현하며 이들을 전부 합하여 '10000000 11001001 00001..'와 같이 표현한다.

그러나 위처럼 표현하면 지수가 음수일 경우 문제가 생긴다. 위처럼 표시하면 지수의 범위는 0~255만을 표현할 수 있기 때문에 음수를 표현할 수 없다. 이를 해결하기 위해 지수가 -127~128의 범위를 표현할 수 있도록 기존의 지수에 127을 더하여 표현한다. 이러한 방식으로 표현하면 '00000000'은 '-127'을 의미하며, '11111111'은 128을 의미하고 '01111111'은 0을 의미한다. 따라서 위에서 지수는 '10000000'으로 표현되며 '3.14159'의 경우 '11000000 01001001 00001..'으로 표현한다.

오차가 생기는 이유

위에서 설명한 컴퓨터에서 부동소수점 방식으로 소수를 저장하는 방식에서 가수부분을 전부 사용하는 것이 아니라 미리 정해놓은 비트의 수 만큼만 사용하고 나머지는 사용하지 않는다. 정확하게는 24번째 비트(단정도 부동소수점의 경우)에서 반올림을 하여 사용하는데(1이면 올림, 0이면 내림), 이러한 과정에서 오차가 발생하는 것이다. 이는 0과 1을 기본으로 사용하는 컴퓨터의 본질적인 한계이기에 어쩔 수 없는 오차인 것이다.

결론

소수를 저장할 때 발생하는 오차는 컴퓨터의 본질적인 한계이다. 이를 방지하고 싶다면 소수를 정수의 형태로 저장한 후 사용할 때 마다 소수처럼 사용하는 방식은 어떨까?