[백준1707] 이분 그래프 / Java

링크 | https://www.acmicpc.net/problem/1707

문제 |

그래프의 정점의 집합을 둘로 분할하여, 각 집합에 속한 정점끼리는 서로 인접하지 않도록 분할할 수 있을 때, 그러한 그래프를 특별히 이분 그래프 (Bipartite Graph) 라 부른다.

그래프가 입력으로 주어졌을 때, 이 그래프가 이분 그래프인지 아닌지 판별하는 프로그램을 작성하시오.

입력 |

입력은 여러 개의 테스트 케이스로 구성되어 있는데, 첫째 줄에 테스트 케이스의 개수 K가 주어진다. 각 테스트 케이스의 첫째 줄에는 그래프의 정점의 개수 V와 간선의 개수 E가 빈 칸을 사이에 두고 순서대로 주어진다. 각 정점에는 1부터 V까지 차례로 번호가 붙어 있다. 이어서 둘째 줄부터 E개의 줄에 걸쳐 간선에 대한 정보가 주어지는데, 각 줄에 인접한 두 정점의 번호 u, v (u ≠ v)가 빈 칸을 사이에 두고 주어진다.

출력 |

K개의 줄에 걸쳐 입력으로 주어진 그래프가 이분 그래프이면 YES, 아니면 NO를 순서대로 출력한다.

• 2 ≤ K ≤ 5
• 1 ≤ V ≤ 20,000
• 1 ≤ E ≤ 200,000

예제 |

입력

2
3 2
1 3
2 3
4 4
1 2
2 3
3 4
4 2

출력

YES
NO

Solution |

• BFS와 DFS를 이용한 방식을 각각 구현하였다.

• 비연결 그래프를 고려하기 위해 모든 정점을 확인해야하므로 모든 정점에서 시작하는 DFS/BFS를 실행한다.

• 방문하지 않은 노드에 그 전 노드와 다른 색을 넣어준다.

• 방문한 정점들 중 연결된 정점의 색이 같은 경우를 check하여 색이 같으면 이분그래프에 부합하므로 false return

• DFS는 재귀함수를 이용하여 boolean이 아닌 void 함수 사용.

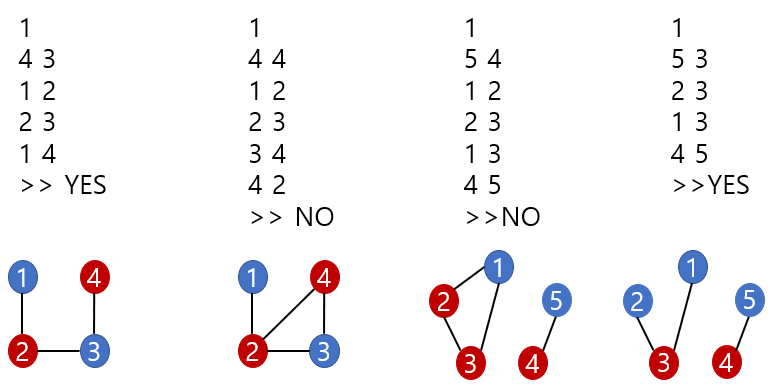
cf) 오류 시 반례 체크

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.LinkedList;
import java.util.StringTokenizer;

public class Bipartite_Graph {
	static int V, E;
	static Node[] nodes;
	static boolean[] visited;
	static boolean ans;
	
	static class Node{
		int idx;
		boolean color;
		// 연결된 리스트_간선
		LinkedList<Node> child = new LinkedList<>(); 
		
		public Node(int idx) {
			this.idx = idx;
		}
		public void setColor(boolean color) {
			this.color = color;
		}
	}
	
	public static void main(String[] args) throws IOException {
		int v, w;
		StringBuilder sb = new StringBuilder();
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));			
			
		int K = Integer.parseInt(br.readLine());
		
		while (K--!=0) {
			StringTokenizer s = new StringTokenizer(br.readLine());		
			V = Integer.parseInt(s.nextToken()); // 정점
			E = Integer.parseInt(s.nextToken()); // 간선
			
			nodes = new Node[V+1];
			visited = new boolean[V+1];
			for(int i=0; i<=V; i++) {
				nodes[i]=new Node(i);
			}

			for (int i=0; i<E; i++) {
				StringTokenizer vw = new StringTokenizer(br.readLine());
				v = Integer.parseInt(vw.nextToken());
				w = Integer.parseInt(vw.nextToken());

				nodes[v].child.add(nodes[w]);
				nodes[w].child.add(nodes[v]);
			}
			
			boolean ans = true;
			//비연결 그래프를 고려하기 위해 모든 정점을 확인해야 함
			
			for(int i = 1; i<=V; i++) {
				if (!visited[i]) {
					visited[i]=true;
					nodes[i].setColor(true);
					//BFS
//					if(!BFS(i)) {
//						ans = false; 
//						break;
//					}
					
					//DFS
					DFS(i);
					if(!ans) {
						break;
					}
				}
			}	
			sb.append(ans?"YES":"NO").append('\n');
		}
		System.out.println(sb);
	}
	
	static boolean BFS(int idx) {
		LinkedList<Node> queue = new LinkedList<>();
		queue.add(nodes[idx]);

		while (!queue.isEmpty()) {
			Node node=queue.poll();
			if(check(node)) {
				return false;
			}else {		
			    for (Node c : node.child) {		    	
			        if (!visited[c.idx]) { 
				        visited[c.idx] = true;
				        // 연결된 이전 정점과 다른 색으로 설정 
				        c.setColor(!node.color);
				        queue.add(c);
				    }
			    }
			}
		}
		return true;
	}
	static void DFS(int idx) {
		if(check(nodes[idx])) {
			ans = false;
			return;
		}else {		
		    for (Node c : nodes[idx].child) {		    	
		        if (visited[c.idx]) { continue;}
		        
			    visited[c.idx] = true;
			    c.setColor(!nodes[idx].color);
			    DFS(c.idx);
		    }
		}
	}
	static boolean check(Node node) {
		for (Node n : node.child) {
			//방문한 적 있고 연결된 정점의 색이 같은 경우 true(이분리스트x)
			if(visited[n.idx] && n.color == node.color) {
				return true;
			}
		}
		return false;
	}
}