[백준10844] 쉬운 계단 수 / Java

링크 | https://www.acmicpc.net/problem/10844

문제 |

45656이란 수를 보자.
이 수는 인접한 모든 자리의 차이가 1이다. 이런 수를 계단 수라고 한다.
N이 주어질 때, 길이가 N인 계단 수가 총 몇 개 있는지 구해보자. 0으로 시작하는 수는 계단수가 아니다.

입력 |

첫째 줄에 N이 주어진다. N은 1보다 크거나 같고, 100보다 작거나 같은 자연수이다.

출력 |

첫째 줄에 정답을 1,000,000,000으로 나눈 나머지를 출력한다.

예제 |

입력           1
출력           9

입력           2
출력           17

Solution |

• i번째 자리에 들어갈 수 있는 숫자를 카운트한다.
  ex) 0 1 2 3만으로 이루어진 세자리수 계단수를 구한다고 가정해보자. 백의 자리에는 0을 제외한 1 2 3이 가능하다. 백의자리가 1인경우 십의자리 숫자에는 0 또는 2만 가능하고, 십의자리가 0일때 일의자리에는 1, 2일때는 1과 3이 가능하다.
  
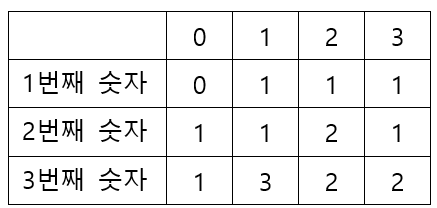
• 0부터 9까지의 숫자를 이용한 계단수를 구하다보니 int의 범위를 초과한다.(int범위 -2^32~2^32)
  결과값에서 1000,000,000을 나눈 나머지를 구하는 것이므로 과정 중간에 각각 1000,000,000으로 %연산을 하여도 무방하다.
• 모듈러연산: 어떤 정수 a를 b로 나눴을때 몫 q 나머지 r은 유일하다. 즉, 유일하게 a=bq+r로 표현된다.
  a=bq+r
  c=Bq+R
  a+c= (b+B)q+r+R
  (a+c) %q= (r+ R)%q
  (a%q+c%q)%q= (r+R)%q
  a와 c를 각각 q로 나눈 나머지값을 더한 것과 a+c를 q로 나눈 나머지 값은 동일하다. 그러므로 해당 프로그램에서 1000,000,000을 위의 식과 같이 나누어 주어도 구하고자 하는 값을 얻을 수 있다.

import java.util.Scanner;

//계산수
public class StepNumber {
	public static void main(String[] args) {
		int N;
	    long cnt=0, mod = 1000000000;
		Scanner input = new Scanner(System.in);
		N = input.nextInt();
		long[][] arr = new long[N+1][10]; //N번째 자리에 0~9 숫자가 들어갈 경우의 수
		
		//첫번째 자리에 들어갈 수 있는 경우의 수는 한개 1~9
		arr[1][0] = 0;
		for (int i=1; i<10; i++) {
			arr[1][i] = 1;
		}
		
		//i번째 지리수가 0일때는 1, 9일때는 8만 가능
		for (int i=2; i<N+1; i++) {
			for (int j=0; j<10; j++) {
				if (j==0) {
					arr[i][0] = arr[i-1][1]% mod;
				}else if(j==9) {
					arr[i][9] = arr[i-1][8]% mod;
				}else {
					arr[i][j] = (arr[i-1][j-1] + arr[i-1][j+1])% mod;
				}
			}
		}
       
		for (int i=0; i<10; i++) {
			cnt += arr[N][i];
		}
		
		System.out.println(cnt%mod);
		input.close();
	}
}