부동소수점(C++)

Kiwoong Park·2023년 6월 17일

출처 : C++ 실력 완성 올인원 패키지 Online.[FastCampus]

부동소수점의 출력

#include <iostream>
using namespace std;
int main() 
{
	float num0 = 1.5;
	float num1 = num0 * 1.5;
	float num2 = num0 / 2;
	float num3 = num0 - 3;

	cout << "num0 " << num0 << endl; // 1.5
	cout << "num1 " << num1 << endl; // 2.25
	cout << "num2 " << num1 << endl; // 0.75
	cout << "num3 " << num1 << endl; // -1.5

}

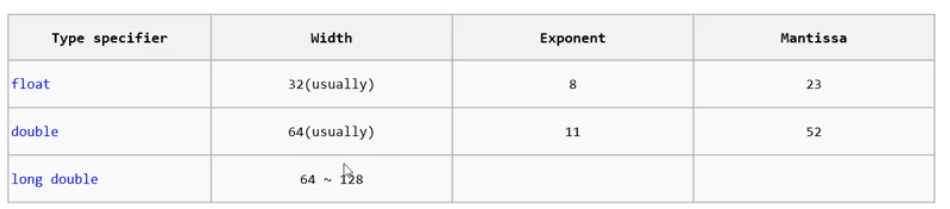
Exponent : 지수부
Mantissa : 가수부

부동소수점 자료형들의 Size

	float num0 = 1.0;
	double dbl = 1.0;
	long double ldbl = 1.0;
    
    // float은 4바이트, double은 8바이트(대부분)
    // 환경에 따라 사이즈가 다를 수 있음(특히 long double)
	cout << sizeof(num0) << endl; // 4byte = 32bit
	cout << sizeof(dbl) << endl; // 8byte = 64bit
	cout << sizeof(ldbl) << endl; // 8byte = 64bit

접미사의 표현 (f:float, none:double, L: long double)

// 리터럴에 어떤 접미사를 붙이는 가에 따라 세부 자료형을 정할 수 있다 

cout << sizeof(1.0f) << endl; // 4
cout << sizeof(1.0) << endl;  // 8 ~ 부동소수점에서는 접미사가 없는 경우 기본적으로 double
cout << sizeof(1.0L) << endl; // 8

IEEE754 ~ 부동소수점을 표현하는 표준

부동소수점의 메모리 표현

음수이고 1보다 큰 경우

위 그림과 같이 2진수로 표현한다.

2진수로 표현한 수를 1.~~ 으로 맞추어 가수부와 지수부로 나눈다.

부호는 그대로 메모리에 쓰고 -> 1(음수), 0(양수)

가수부는 32bits 메모리의 경우 뒤 23bits에 그대로 쓴다 -> 110110101+나머지 bit는 0으로

지수부의 경우 기준 값은 127이 0이다(?)
그 이유는, 예제에서는 2^6을 표현하였는데 실제로 2^(음수), Ex. 2^(-6)인 경우도 표현해야 하기 때문이다. 만약 그냥 2^6을 00000110 (2)로 표현한다면 2^(-6)을 8bits상에 표현할 수 없을 것이다.
물론 2의 보수 등을 취하는 방법을 사용할 수 있으나 부동소수점의 경우 그러한 전략을 취하지는 않았다.

127을 0으로 간주하고 2(10)의 6제곱이므로 6을 더하면 133이 되며,
이를 비트로 표현하면 10000101 // 128 + 4 + 1

양수이고 1보다 작은 경우

위 그림과 같이 가수부는 그대로 쓰고, 지수부는 127-3= 124를 비트로 표현하여 01111100(2) 을 지수부로 표현한다.

	unsigned int unum;
	float fnum = 0.231689453125f;
	memcpy(&unum, &fnum, sizeof(fnum)); // fnum에 있는 값을 unum으로 카피한다. unum = fnum 과 다른 결과 

	cout << unum << endl; // 1047347200 -> 0|01111100|11011010100000000000000(2)
	cout << fnum << endl; // 0.231689

부동소수점의 크기 비교

0.1f와 같은 수는 2진수로 정확히 표현할 수 없기 때문에 가장 근사한 수로 나타내게 된다.
오차율로 인해 정확한 크기 비교가 불가능하기 때문에 부동소수점으로 크기 비교를 할 때는 항상 유의해야 한다.

	float n0 = 0.1f;
	float n1 = 0.02f * 5.0f;

	if (n0 == n1) // False
		cout << "Equal 1" << endl;
	if (n0 == 0.1f) // True
		cout << "Equal 2" << endl;
	if (n0 == 0.1) // False float의 0.1과  double의 0.1은 실제 다름
		cout << "Equal 3" << endl;
	if (n0 == 0.1L)
		cout << "Equal 4" << endl;


	cout.precision(64);
	cout << n0 << endl; // 0.100000001490116119384765625 ~ 십진수 0.1f은 2진수로 표현할 수 없기 때문에..
	cout << n1 << endl; // 0.0999999940395355224609375
	cout << 0.1 << endl; // 0.1000000000000000055511151231257827021181583404541015625
	cout << 0.1L << endl; // 0.1000000000000000055511151231257827021181583404541015625

부동소수점 오차의 누적

#include <iostream>
#include <cfloat>
using namespace std;
int main() 
{
	float n0 = 1.0f;
	float n1 = 0.0f;
	for (int i = 0; i < 1000; i++)
		n1 = n1 + 0.001;
	if (n0 == n1)  // False
		cout << "Equal0" << endl;
	if (fabsf(n0 - n1) <= FLT_EPSILON) // False
		cout << "Equal 1" << endl;
	
}

위 코드와 같이 2진수로 표현할 수 없는 숫자를 누적해서 더하는 경우 오차가 쌓이면서 Epsilon으로도 제대로된 크기 비교를 할 수가 없다.

Epsilon 크기 구하기

0 표현하기

#include <iostream>
#include <cfloat>
using namespace std;
int main() 
{
	unsigned int num0 = 0b00111111100000000000000000000000;
	float num1;
	memcpy(&num1, &num0, sizeof(num0));
	cout.precision(64);
	cout << "num1 " << num1 << endl; // num1 1;
	
}

float의 가장 작은 수 표현하기

#include <iostream>
#include <cfloat>
using namespace std;
int main() 
{	
	unsigned int num2 = 0b00111111100000000000000000000001; // 0보다 가수부로 1큰 수
	float num3;
	memcpy(&num3, &num2, sizeof(num2));
	cout.precision(64);
	cout << "num3 " << num3 << endl; // num3 1.00000011920928955078125;

	cout << num3 - num1 << endl; // 1.1920928955078125e-07
	cout << FLT_EPSILON << endl; // 1.1920928955078125e-07 float로 표현할 수 있는 가장 작은 수가 Epsilon 값이 된다.

}

수를 더했지만 값은 그대로입니다?!

1.0에 더할 수 있는 최솟값을 더하면?

int main()
{
	float num0 = 1.0f;
    
    unsigned int num1 = 0b00110100000000000000000000000000;
    float num2;
    memcpy(&num2, &num1, sizeof(num1));
    
    cout.precision(64);
    cout << num0 + num2; // 1.00000011920928955078125
    
}

// 0011,1111,1000,0000,0000,0000,0000,0000 = 1.0(2) (32bits 가정 시) 
// 2^(-23)을 32bits 로 표현하면 지수부는 127-23 = 104 이므로 
// 0011,0100,0000,0000,0000,0000,0000,0000 = 1.0(2) * 10^(-23)

int main()
{
	float num0 = 1.0f;
    
    unsigned int num1 = 0b00110011100000000000000000000000;
    float num2;
    memcpy(&num2, &num1, sizeof(num1));
    
    cout.precision(64);
    cout << num0 + num2; // 1
    
}
// 0011,0011,1000,0000,0000,0000,0000,0000 = 1.0(2) * 10^(-24) 를 더한다면?
// 더한 수를 인지 못하고 그냥 1이 출력된다.
// 1.000...00001인데 가수부가 24bit로 23bit 0에서 잘리게 되기 때문

1에 다 10(2)^23을 더하면?

int main()
{
	float num0 = 1.0f;
    
    unsigned int num1 = 0b01001011000000000000000000000000;
    float num2;
    memcpy(&num2, &num1, sizeof(num1));
    
    cout.precision(64);
    cout << num2 << endl; // 8388608 = 2^23
    cout << num0 + num2 << endl; // 8388609 = 2^23 + 1    
}
// 0100,1011,0000,0000,0000,0000,0000,0000 = 1.0(2) * 10^23(2)

1에 10(2)^24을 더하면?

int main()
{
	float num0 = 1.0f;
    
    unsigned int num1 = 0b01001011100000000000000000000000;
    float num2;
    memcpy(&num2, &num1, sizeof(num1));
    
    cout.precision(64);
    cout << num2 << endl; // 16777216
    cout << num0 + num2 << endl; // 16777216
    
}
// 0100,1011,1000,0000,0000,0000,0000,0000 = 1.0(2) * 10^24(2)
// 1이 더해지지 않고 버려진다.

즉 큰 수에서는 작은 수를 더하면 버려지기 때문에, 큰 수를 표현하면서 정밀도가 필요하다면 다른 라이브러리나 정수형을 활용해야 된다!

최대값?

#include <iostream>
#include <cfloat>
#include <cstring>
using namespace std;

int main()
{
	float num0 = FLT_MAX;
    
    cout.precision(64);
    cout << num0 << endl;
    
    float num1;
    // unsigned int num2 = 0b01111111111111111111111111111111; // nan
    // unsigned int num2 = 0b01111111011111111111111111111111; // 최대값
     unsigned int num2 = 0b01111111100000000000000000000000; // inf
    memcpy(&num1, &num2, sizeof(num2));
    
    cout << num1 << endl;
    
    // 340282346638528859811704183484516925440
    // nan ~ 지수부 비트가 다 켜져있으면 다른 취급을 함.
    // 지수부 비트가 다 켜져있고, 가수부 비트가 하나라도 켜져 있으면 nan 취취급을
    // 최대 max값은 지수값을 하나만 내린 것으로 
    // 0b01111111011111111111111111111111; 이 경우 아래 값이 나옴
    // 340282346638528859811704183484516925440
    
    // 또, 지수부가 전부 1로 세팅되고 가수부가 전부 0으로 세팅되면 inf 가 나옴
}

최소값?!

#include <iostream>
#include <cfloat>
#include <cstring>
using namespace std;

int main()
{
	float fltMin = FLT_MIN;
	unsigned int ifltMin;
	memcpy(&ifltMin, &fltMin, sizeof(fltMin));
	
	float fltTrueMin = FLT_TRUE_MIN;
	unsigned int ifltTrueMin;
	memcpy(&ifltTrueMin, &fltTrueMin, sizeof(fltTrueMin));

    cout << fltMin << endl; // 1.17549e-38
    cout << fltTrueMin << endl; // 1.4013e-45
    cout << ifltMin << endl; // 8388608 
    // 0000,0000,1000,0000,0000,0000,0000,0000 즉 지수비트가 1인 경우 = 10^(-126)(2)
    cout << ifltTrueMin << endl; // 1
    // 0000,0000,1000,0000,0000,0000,0000,0000 즉 가수비트가 1인 경우 = 10^(-126)(2) * 10^(-23)(2)
    // 지수 비트가 다 0 인 경우 1.~ 으로 가정하지 않고 0.~~으로 가정함.
    
    
    
}

Kiwoong Park

You matter, never give up

이전 포스트

정수형(C++)

다음 포스트

부동소수점(C++)

부동소수점의 출력

부동소수점 자료형들의 Size

접미사의 표현 (f:float, none:double, L: long double)

IEEE754 ~ 부동소수점을 표현하는 표준

부동소수점의 메모리 표현

음수이고 1보다 큰 경우

양수이고 1보다 작은 경우

부동소수점의 크기 비교

부동소수점 오차의 누적

Epsilon 크기 구하기

0 표현하기

float의 가장 작은 수 표현하기

수를 더했지만 값은 그대로입니다?!

최대값?

최소값?!

정수형(C++)

printf

0개의 댓글