[leetcode]221.Maximal Square

문제

Given an m x n binary matrix filled with 0's and 1's, find the largest square containing only 1's and return its area.

예제

• Example 1:

  	- Input: matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
  	- Output: 4

• Example 2:

  	- Input: matrix = [["0","1"],["1","0"]]
  	- Output: 1

• Example 3:

  	- Input: matrix = [["0"]]
  	- Output: 0

제한사항

Constraints:

m == matrix.length
n == matrix[i].length
1 <= m, n <= 300
matrix[i][j] is '0' or '1'.

풀이

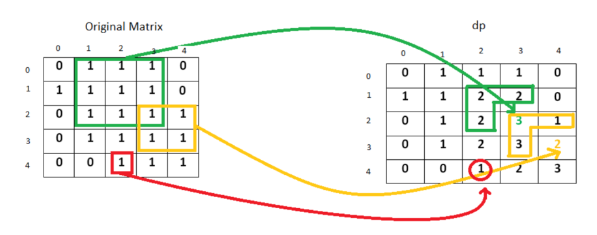
정사각형의 최대 개수를 찾는 것이다.
00부터 nn을 확인하는데 해당 칸의 왼쪽, 위쪽, 왼쪽 대각선을 확인해서 가장 작은 dp값의 + 1 을 해준다.

위 사진을 보고 정확하게 깨닫을 수 있었다.

var maximalSquare = function(matrix) {
    const row=matrix.length;
    const column=matrix[0].length;
 
    if(row<=1&&column<=1){
        return matrix[0][0]
    }
  
    const dp= Array.from({length:row},()=>Array.from({length:column},()=>0))
    
    let max=0;
    for(let i=0 ;i<column;i++){
        if(matrix[0][i]=="1"){
            max=1;
            dp[0][i]=1}
  
    }
    for(let i=0 ;i<row;i++){
        if(matrix[i][0]=="1"){
            max=1;
            dp[i][0]=1}
    }
    
    
    for(let i=1 ;i<row;i++){
        for(let j=1;j<column;j++){
            if(matrix[i][j]=="1"){
                dp[i][j]=Math.min(dp[i][j-1], dp[i-1][j], dp[i-1][j-1])+1;
                max=max<dp[i][j]?dp[i][j]:max
            }
        }
    }

    return max*max
};

dp를 처음 만들 때 첫 Column과, 첫 row를 이용하게 되는데, 그게 전부일 수도 있기 때문에, 예외처리를 해주었다.