트리

• 그래프 중 하나로 정점과 간선으로 이루어져 있고, 트리 구조로 배열된 일종의 계층적 데이터의 집합

구성

• 루트 노드
  • 가장 위에 있는 노드
    • 트리를 탐색할 때 보통 루트 노드를 중심으로 탐색한다.
  • 내부노드
    • 루트 노드와 내부 노드 사이에 있는 노드
  • 리프노
    • 자식 노드가 없는 노드

특징

1. 부모, 자식 계층 구조를 가진다.
2. V - 1 = E라는 특징이 있다.
   • 간선 수 = 노드수 -1
3. 트리 내의 어떤 노드와 어떤 노드까지의 경로는 반드시 존재한다.

종류

• 이진트리: 모든 node의 child nodes의 갯수가 2 이하인 트리
• 정이진트리 : 자식 노드가 0 또는 두개인 이진트리
• 완전 이진 트리: 왼쪽에서부터 채워져 있는 이진 트리, 마지막을 제외하고는 모든 레벨이 채워져 있으며, 마지막 레벨의 경우 왼쪽 부터 채워져 있다.
  
• 변질 이진 트리: 자식 노드가 하나 밖에 없는 이진트리
• 포화 이진 트리 : 모든 노드가 꽉 차 있는 이진트리
• 균형 이진 트리 : 왼쪽과 오른쪽 노드의 높이 차이가 1 이하인 이진 트리 map, set을 구성하는 레드 블랙 트리는 균형 이진 트리 중 하나이다.
  • AVL트리
  • Red-black tree

이진 탐색 트리(BST)

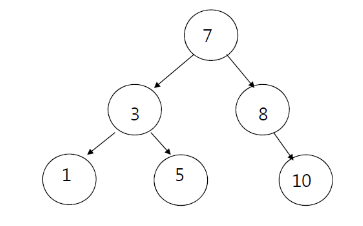
• 이진탐색트리(Binary Search Tree; BST)는 저장과 동시에 정렬을 하는 자료구조
• 어느 node를 선택하든 해당 node의 left subtree에는 그 node의 값보다 작은 값들을 지닌 node들로만 이루어져 있고, node의 right subtree에는 그 node의 값보다 큰 값들을 지닌 node들로만 이루어져 있는 binary tree입니다.
  

조건

1. root node의 값보다 작은 값은 left subtree에, 큰 값은 right subtree에 있다.
2. subtree도 1번 조건을 만족한다.(Recursive)

• 검색과 삽입, 삭제의 시간복잡도는 모두 $O(logn)$이고, worst case는 한쪽으로 치우친 tree가 됐을 때 $O(n)$입니다(Linked list와 다를게 없어지기때문).

AVL트리

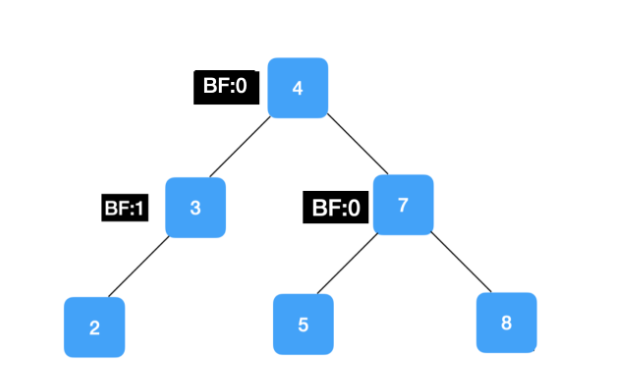
• BST가 최악의 경우 선형적인 트리가 되는 것을 방지하고 스스로 균형을 잡는 이진 탐색트리
  • 두 자식 서브트리의 높이는 항상 최대 1만큼 차이가 난다.
  • 탐색, 삽입, 삭제 모두 시간 복잡도가 O(logn)
  • 삽입, 삭제를 할 때마다 균형이 안맞는 것을 맞추기 위해 트리 일부를 왼쪽 도는 혹은 오른쪽으로 회전시키며 균형을 맞춘다.

레드 블랙 트리

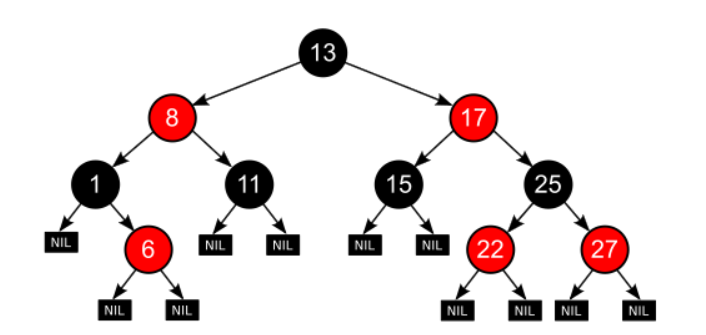
• 균형 이진 탐색 트리로 탐색, 삽입 삭제 모두 시간 복잡도가 O(logn)입니다.
• 각 노드는 빨간색 또는 검은색의 색상을 나타내는 추가 비트를 저장하며, 삽입 삭제 중에 트리가 균형을 유지하도록 하는데 사용된다.

정의

• 각 노드의 색은 red 또는 black이다.
• root 노드는 black이다.
• 모든 말단노드(leaf node)는 black이다.(NIL이 black이 된다.)
• red 노드의 자식노드들은 전부 black이다.(즉, red 노드는 연속되어 등장할 수 없다.)
• Root 노드에서 시작해서 자손인 leaf 노드에 이르는 모든 경로에는 동일한 개수의 black노드가존재한다.

힙

이미지 출처 : https://velog.io/@yanghl98/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-Heap%ED%9E%99-%EA%B0%9C%EB%85%90-%EC%A2%85%EB%A5%98-%ED%99%9C%EC%9A%A9-%EC%98%88%EC%8B%9C-%EA%B5%AC%ED%98%84

• 완전 이진 트리 기반의 자료구조

종류

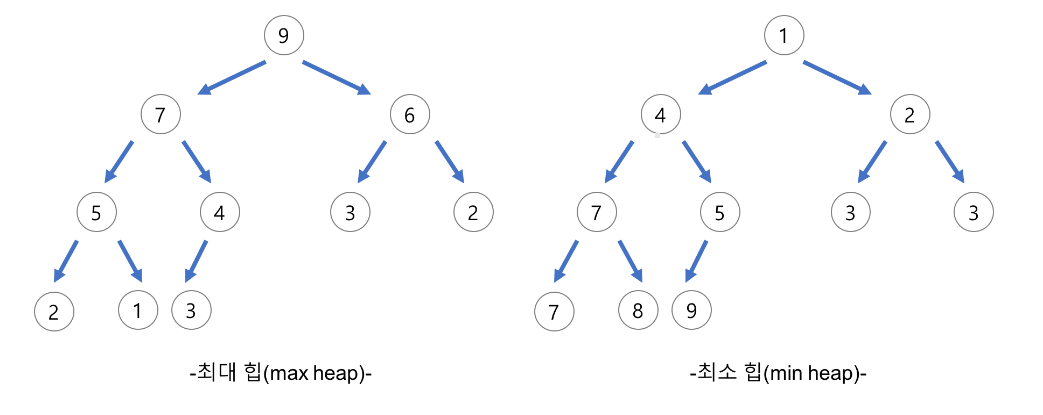
• 최소힙
  • 각 node에 저장된 값은 child node들에 저장된 값보다 작거나 같다 ⇒ root node에 저장된 값이 가장 작은 값이 된다.
    
• 최대힙
  • 각 node에 저장된 값은 child node들에 저장된 값보다 크거나 같다 ⇒ root node에 저장된 값이 가장 큰 값이 된다.
    

Heap 구현

• 트리는 보통 Linked list로 구현합니다. 하지만 Heap은 tree임에도 불구하고 array를 기반으로 구현해야 합니다. 그 이유는 새로운 node를 힙의 ‘마지막 위치’에 추가해야 하는데, 이 때 array기반으로 구현해야 이 과정이 수월해지기 때문입니다.
  • 구현의 편의를 위해 array의 0번 째 index는 사용하지 않습니다.
  • 완전이진트리의 특성을 활용하여 array의 index만으로 부모 자식간의 관계를 정의합니다.
    • $n$번 째 node의 left child node = $2n$
    • $n$번 째 node의 right child node = $2n+1$
    • $n$번 째 node의 parent node = $n/2$
• push - $O(logn)$
  • heap tree의 높이는 $logN$입니다.
  • push() 를 했을 때, swap하는 과정이 최대 $logN$번 반복되기 때문에 시간복잡도는 $O(logn)$입니다.
  • 새로운 노드를 힙의 마지막 노드에 이어서 삽입하고 이 노드를 부모 노드 들과의 크기를 비교하며 교환해서 힙의 성질을 만족시킨다.
• pop - $O(logn)$
  • pop()을 했을 때, swap하는 과정이 최대 $logN$번 반복되기 때문에 시간복잡도는 $O(logn)$입니다.
  • 루트 노드가 삭제되고, 그 이후 마지막 노드와 루트 노드를 스왑하여 스왑 과정을 거쳐 재구성한다.