백준 Java 9095_1,2,3 더하기

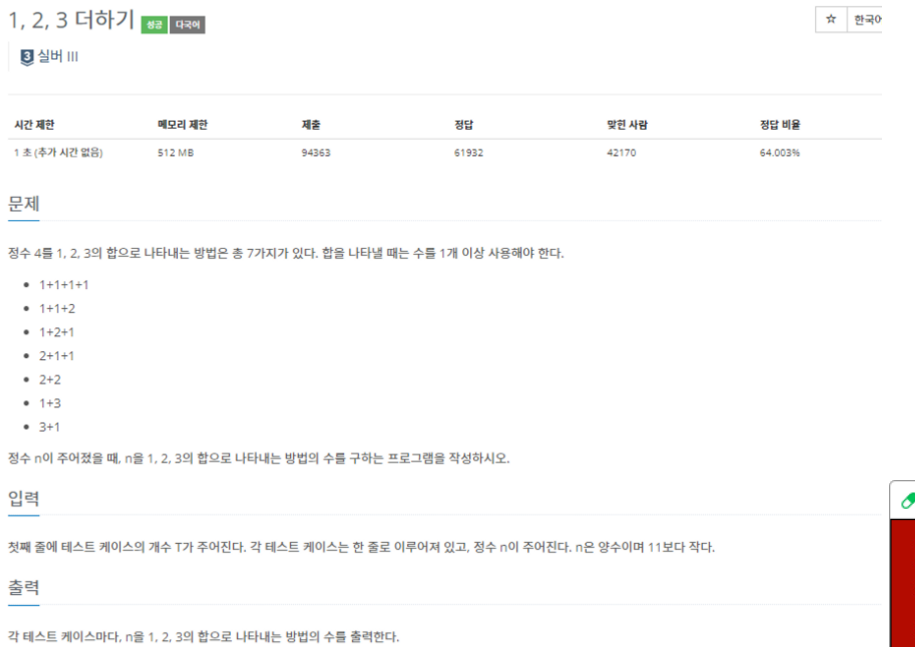
• 1 ={1}로 한 개, 2 = {1+1, 2}로 2개, 3 = {1+1+1, 1+2, 2+1, 3}으로 4개이다.
• 각 경우의 수에 1, 2, 3만을 더해주므로 전체적인 경우의 수는 변합이 없게 되고 결과적으로 4 + 2 + 1로 7개라는 경우의 수가 발생한다.
• 따라서, 점화식은 dp [n] = dp [n-1] + dp [n-2] + dp [n-3] 이된다.

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringBuilder sb = new StringBuilder();
        int k = Integer.parseInt(br.readLine());

        while (k > 0) {
            int p = Integer.parseInt(br.readLine());
            int[] dp = new int[100];
            dp[1]=1;
            dp[2]=2;
            dp[3]= 4;
            for (int i = 4; i < p +1; i++) {
                dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3];
            }
            sb.append(dp[p]).append("\n");
            k--;
        }

        System.out.println(sb);

    }
}