백준 Java 11057_오르막 수

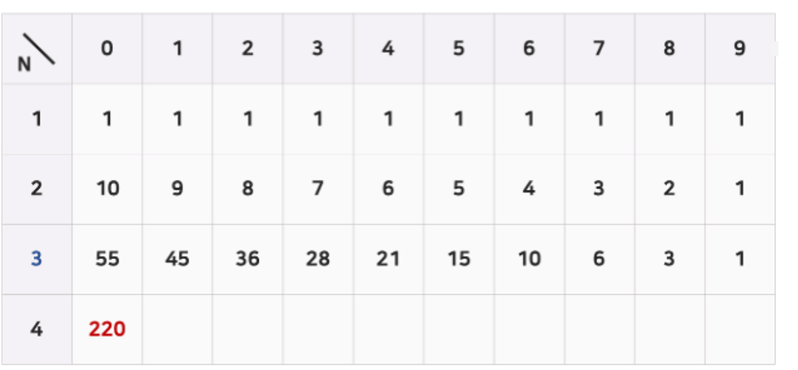
N=1 한자릿수일 경우 0~9까지 각 숫자들을 한 번씩 이용해 총 10가지의 오르막수를 만들 수 있다.

N=2 두자릿수일 경우

00, 01, 02 ... 09 -> 10 가지

11, 12, 13 ... 19 -> 9가지

22, 23 ... 29 -> 8가지

...

88, 89 -> 2가지

99 -> 1가지

로 총 55가지의 오르막수를 만들 수 있다.

즉, 0~9까지의 각 숫자(j)에서 만들 수 있는 오르막수는 이전 자릿수 N-1에서의 j부터 마지막 9까지의 합이다.

자릿수가 1인 경우, 각 숫자에서의 dp값이 모두 1 -> 이를 초기값으로 지정해줌

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

public class Main {
    static int[][] dp;
    static long[]result;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int k = Integer.parseInt(br.readLine());
        result = new long[k+1];
        dp = new int[k + 1][10];
        for (int i = 0; i < 10; i++) {
            dp[1][i] =1;
        }
        result[1] = 10;
        for (int i = 2; i <= k; i++) {
            for (int j = 0; j < 10; j++) {
                if (j == 0) {
                    dp[i][j] = dp[i - 1][j];
                }
                else {
                    dp[i][j] = dp[i][j - 1] + dp[i - 1][j];
//맨 마지막에 정답을 출력할 때만 나누어주면 된다고 생각했다.하지만 dp계산 후에도 나머지연산을 해줘야 한다.
//왜냐하면 자릿수가 40만 넘어가도 값이 한참 클터이니 dp후에도 모듈러 연산을 해준다
                    dp[i][j] %= 10007;
                }
                result[i] += dp[i][j];
            }
        }

        System.out.println(result[k] %10007);
        }
        }

참조 : https://minhamina.tistory.com/147