1. 자료구조(Data Structure)
들어가기 앞서
❓ 자료구조와 알고리즘을 왜 배워야 할까?!
- 코드에 버그도 없고 배포까지 마쳤는데, 실행 시 왜 이렇게 느리지..?!
- 다른사람들과 협업하기에 더 편하고 효율적인 코드가 필요해!
- 관리하기 편하고 효율적인 코드!
-> 이를 위해 필요한 지식임
1) 자료구조란?
- 데이터를 정리하는 것!
-> 스피드에 바로 영향을 줌 - 어떤 작업에 어떤 데이터 구조를 언제, 어떻게 쓰는지 아는 것이 스피드를 결정하게 됨!
- 각각의 데이터 구조에 대한 이해도가 필요함
- 데이터 구조의 이해에 필요한 4가지 오퍼레이션 상황
- 읽기 Read
- 검색 Search
- 삽입 Insert
- 삭제 Delete
2) 배열(Array)
-
시간복잡도(Time Complexity) : 데이터 구조의 오퍼레이션 혹은 알고리즘이 얼마나 빠르고 느린지 측정하는 방법
-
실제 시간으로 측정 X, 얼마나 많은 단계(Steps)가 있는가로 측정 O
-
메모리
- 휘발성(volatile) 메모리 : ex) 메모리 RAM(Random Access Memory)
- 비휘발성(non-volatile) 메모리 : ex) 하드 드라이브
-
오퍼레이션 4가지
- 읽기 Reading : 배열을 어떻게 읽는가
- 0부터 인덱싱(순서가 0부터 시작)
- 배열의 장점은 읽기! (많은 자료를 읽어야 할 때 유용)
- 검색 Searching
- 배열의 단점(오래 걸림) - 선형 검색(Linear Search)
(배열에 해당 데이터가 있긴 한지? 있다면 어디에 있는지? 아무것도 몰라서 하는게 검색이라 전부다 체크해야하기 때문)
- 삽입 Insert(Add)
- 오래 걸릴 수 있음
(기존의 데이터를 밀고 그자리에 넣거나,
기존 배열에 데이터가 꽉 차있는데 거기에 데이터를 더 추가하고싶으면 배열 수를 늘리는것부터 해야함)
- 삭제 Delete
- 삽입과 유사
2. 알고리즘(Algorithm)
1) 알고리즘이란?
- 알고리즘 : 여러개의 지시사항(따라야하는 절차/스텝들)
- 목적을 달성하기 위한 여러개의 행동들 -> 동일한 결과 산출
- ex)
- 지도를 통해 최단거리 길찾기
-> Path Finder Algorithm - 이미지 퀄리티 손상 없이 어떻게 압축할까?!(압축 알고리즘)
-> Compression Algorithm - 데이터 암호화(암호화 알고리즘)
- 지도를 통해 최단거리 길찾기
- 어떤 알고리즘은 특정 자료구조에서만 사용 가능함
2) 이진검색 알고리즘(Binary Search)
- '검색 알고리즘'의 한 종류
- 이진 : '반으로 쪼개는 것'
- 검색을 인덱스 중간에서 시작함, 그다음도 남은 배열의 중간부터 시작함
- 모든 배열에 쓸 순 없음(정렬된 배열(Sorted Array)에만 사용 가능)
- Sorted Array : 순서대로 정렬된 배열(작은 수부터 큰 수 등)
- 정렬된 배열은 insert, delete이 비교적 오래 걸림
-> 이진검색 알고리즘은 선형검색보다 빠르지만, 배열 정렬이 선행되어야 함
3) 선형검색 알고리즘(Linear Search)
- '검색 알고리즘'의 한 종류
- 가장 자연스러운 방법(처음부터 끝까지 순서대로)
- Linear Time Complexity (검색 수행시간과 배열은 정비례)
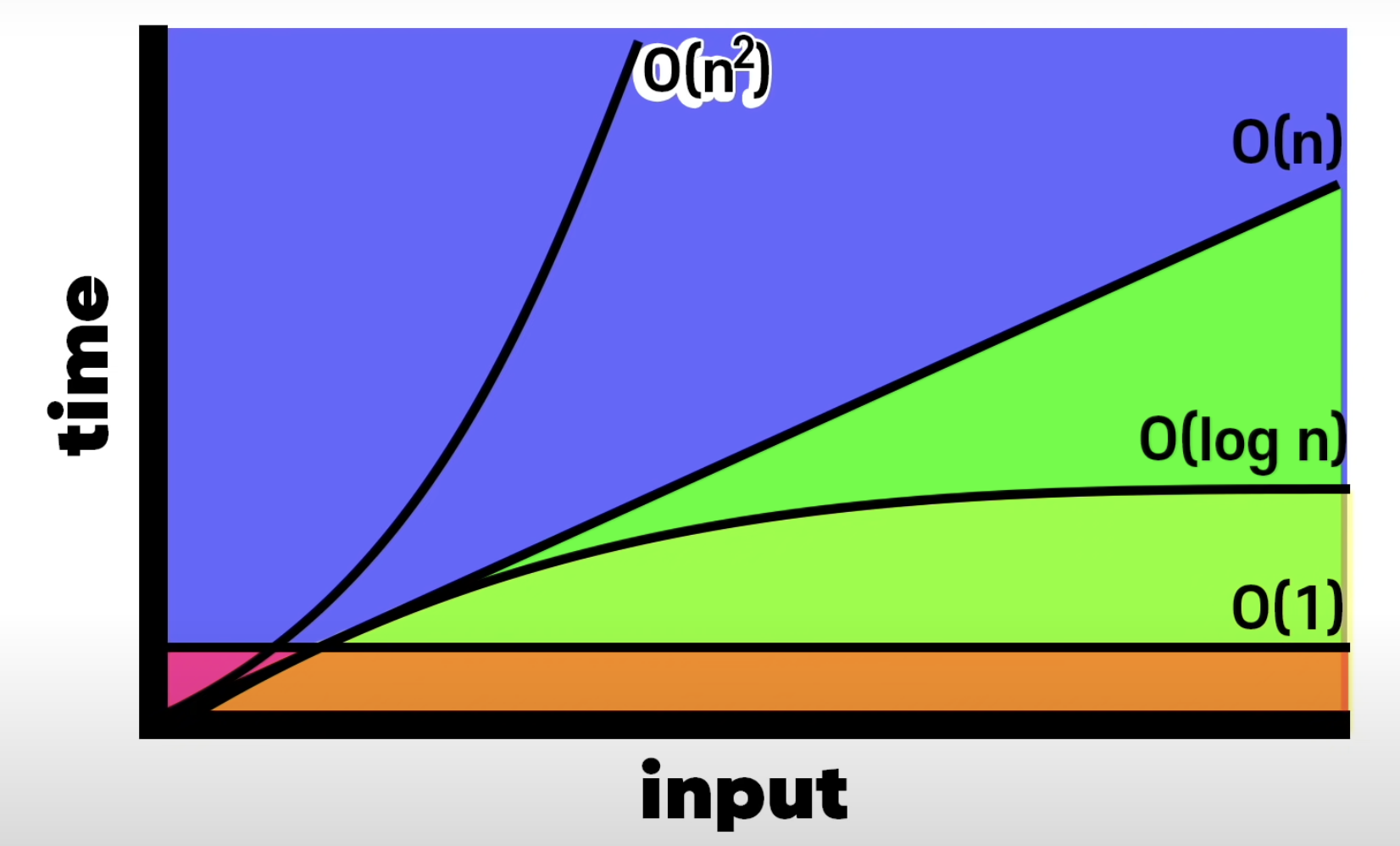
4) 알고리즘 스피드의 표현법 'Big O'
- 알고리즘 스피드 - '완료까지 걸리는 절차의 수'로 결정 됨!
- ex) 선형검색의 시간 복잡도 = O(N)
(Linear Search Algorithm has a time complexity of O of N)
= Big O - Big O - 시간복잡도를 빠르게 설명할 수 있음
ex 1)
def print_first(arr):
print(arr[0])Array = ["kimchi1", "pizza2", ..., "galbi100"]
-> 해당 함수는 1번이면 실행 끝남
(인풋 수에 상관없이 동일한 수의 스텝 필요)
-> 이 함수의 시간복잡도 = constant time(상수 시간)
-> O(1)
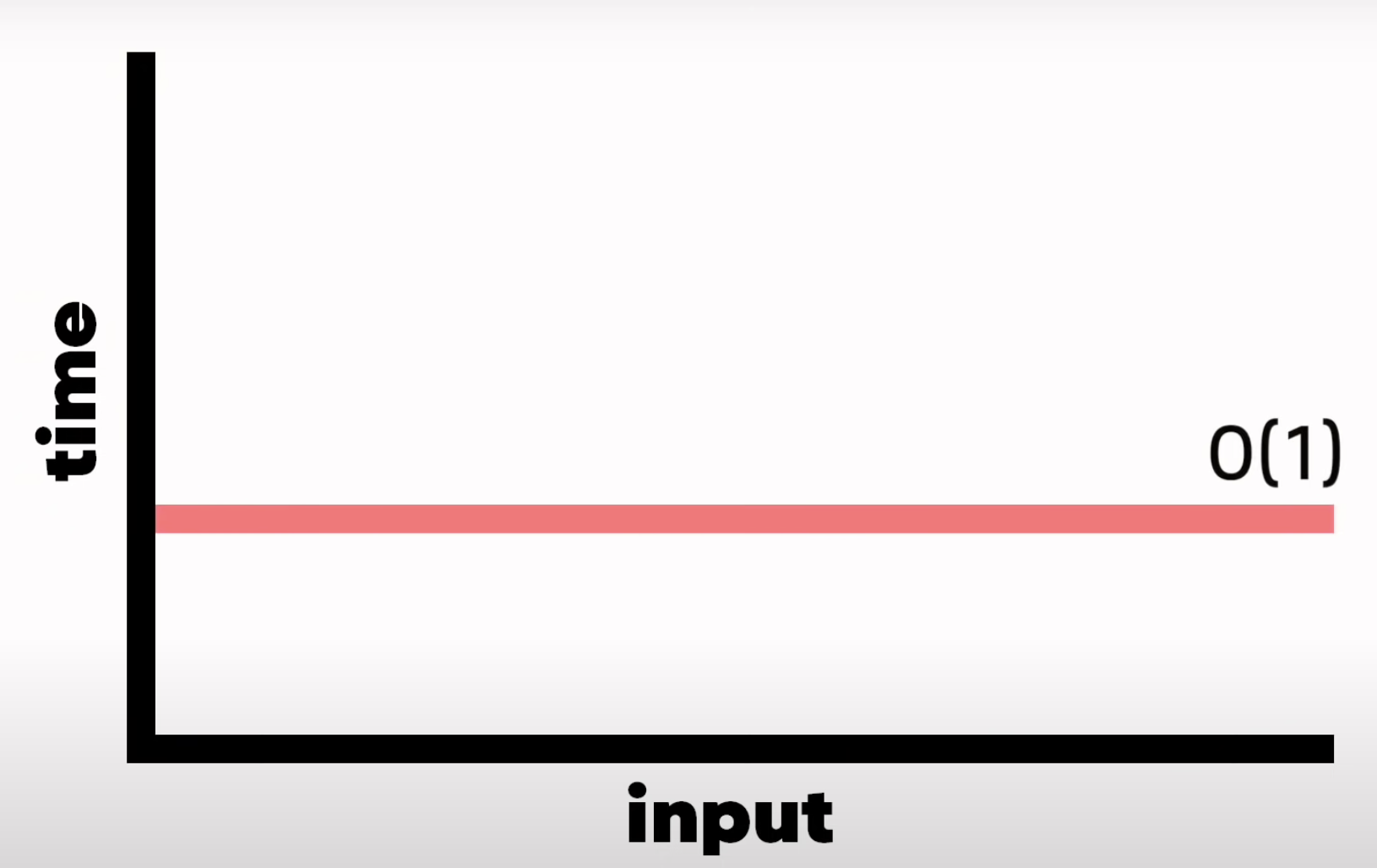
(출처 : 노마드코더 youtube)
ex2)
def print_all(arr):
for n in arr:
print(n)Array = ["kimchi1", "pizza2", ..., "pasta10"]
-> n개 아이템이면 n번 프린트 -> 선형 검색과 유사
-> O(N)
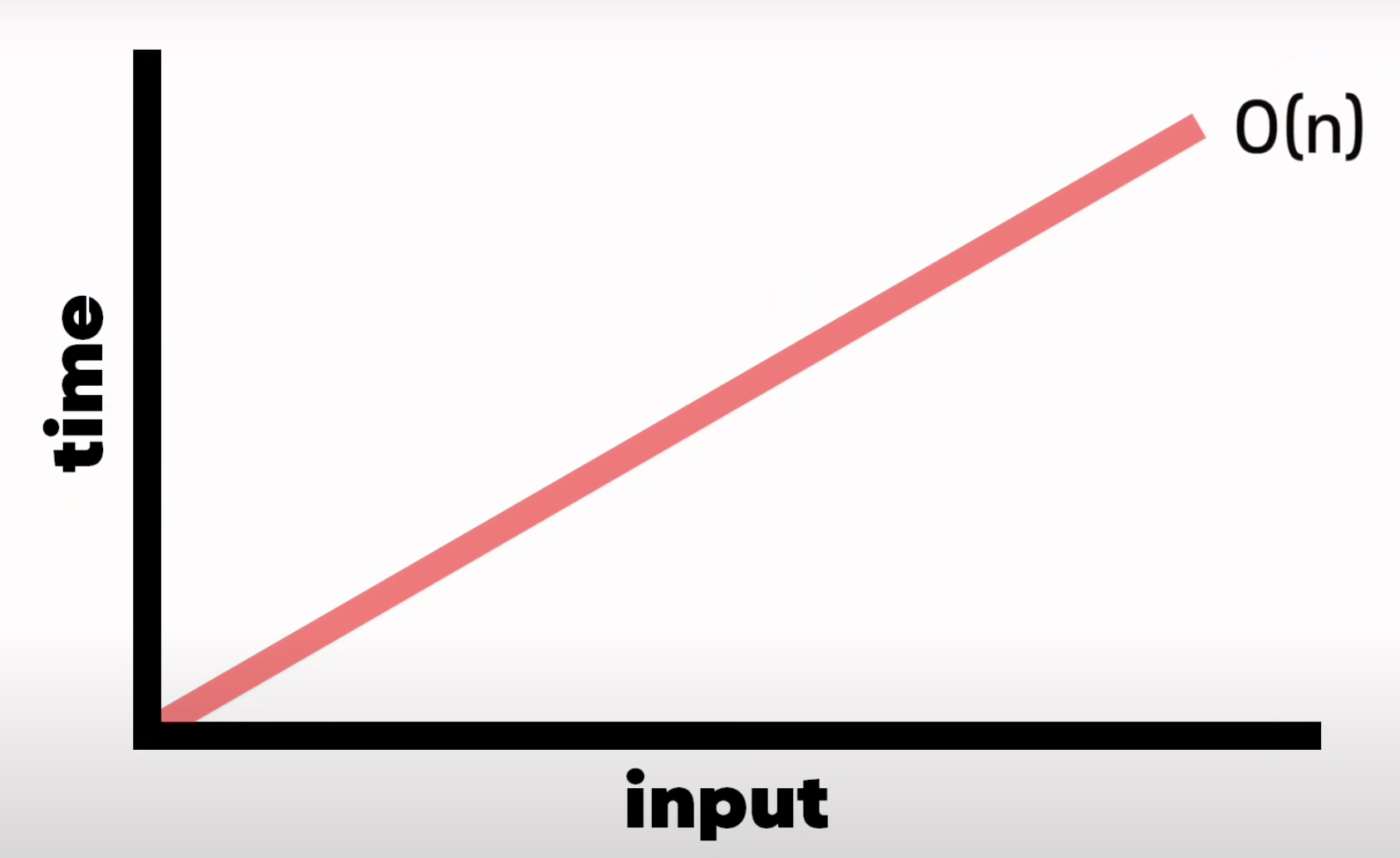
(출처 : 노마드코더 youtube)
- Quadratic Time(2차 시간)
- 중첩 반복(Nested Loops)이 있을 때 발생
def print_twice(arr):
for n in arr:
for x in arr:
print(x, n)
/* 배열의 각 아이템에 대해 루프를 반복 실행 */-> 시간복잡도 : 인풋의 n^2
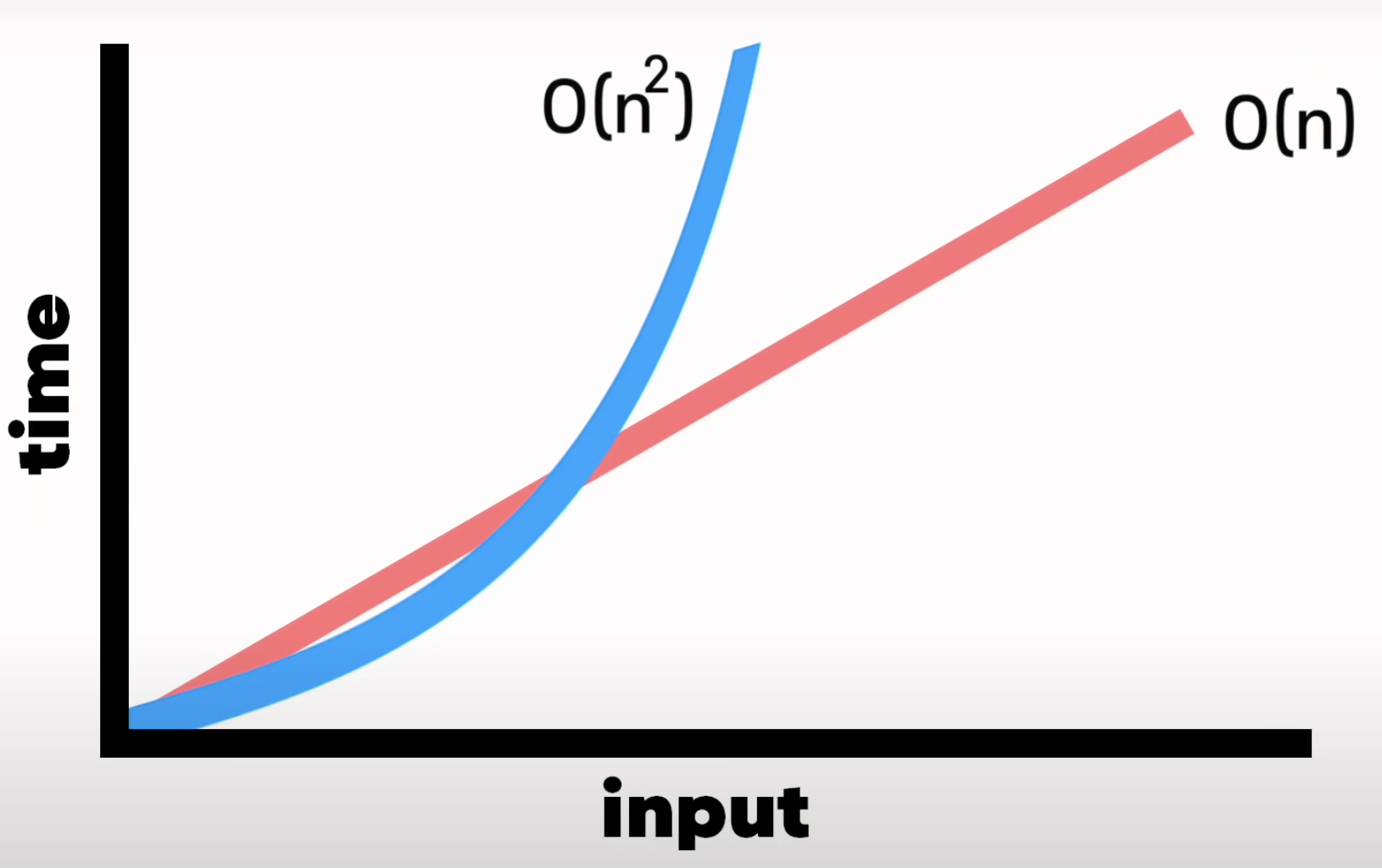
(출처 : 노마드코더 youtube)
- 로그 시간(Logarithmic time)
- 이진검색 알고리즘 설명 시 사용
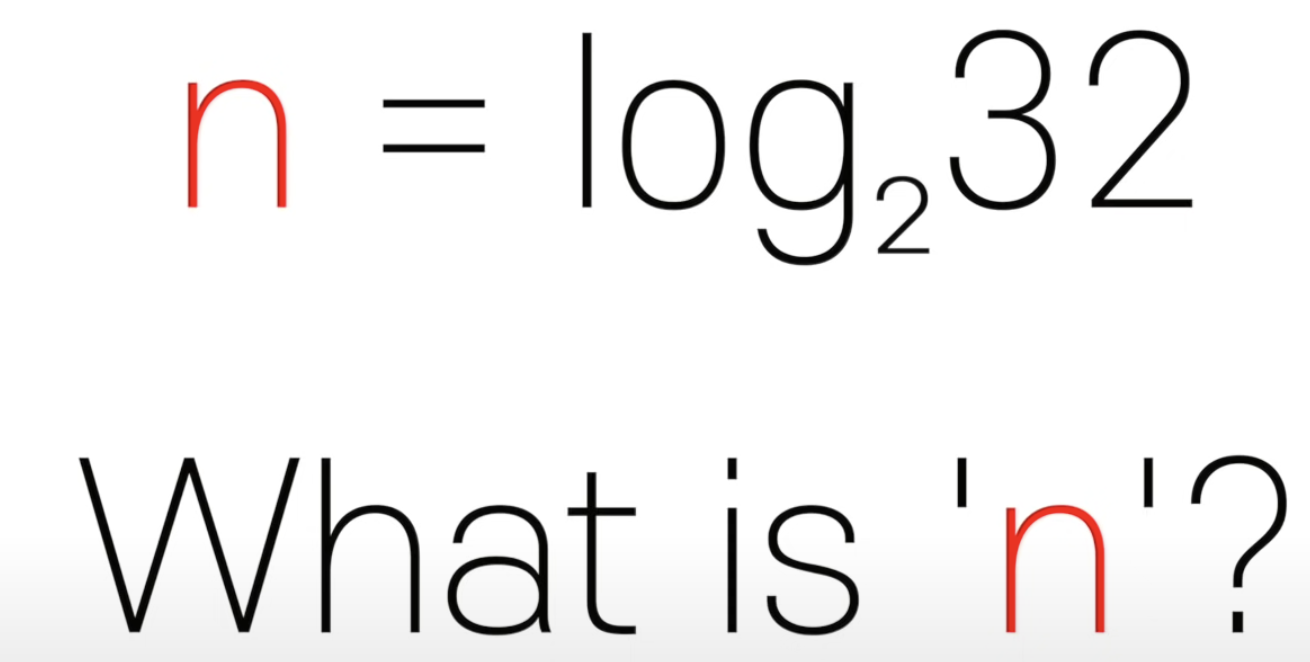
- 이진검색의 시간복잡도 = O(log n)
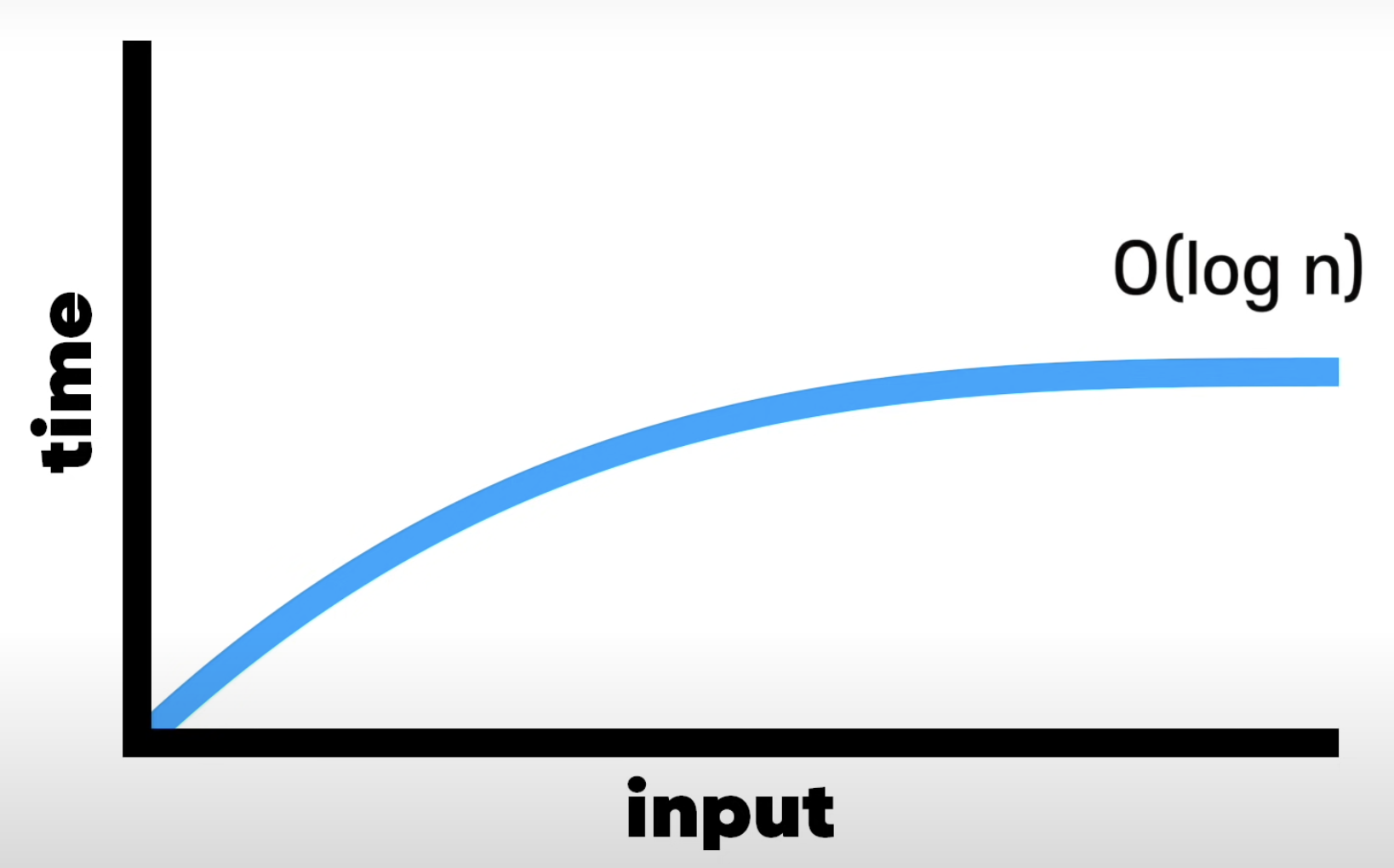
- 이진검색 알고리즘 설명 시 사용
- Big O 의 비교