Pytorch 기초 - 로지스틱 회귀

데이터셋 로드

로지스틱 회귀 - 이진 분류를 수행하는 함수를 학습하는 알고리즘

선형 계층 → sigmoid통과해 0~1 사이 값 추출 → 0.5를 기준으로 참 / 거짓 판단

BCE loss function 사용해 학습

import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.datasets import load_breast_cancer

cancer = load_breast_cancer()
print(cancer.DESCR)
'''
.. _breast_cancer_dataset:

Breast cancer wisconsin (diagnostic) dataset
--------------------------------------------

**Data Set Characteristics:**

...

prognosis via linear programming. Operations Research, 43(4), pages 570-577, 
     July-August 1995.
   - W.H. Wolberg, W.N. Street, and O.L. Mangasarian. Machine learning techniques
     to diagnose breast cancer from fine-needle aspirates. Cancer Letters 77 (1994) 
     163-171.
'''

df = pd.DataFrame(cancer.data, columns = cancer.feature_names)
df.head()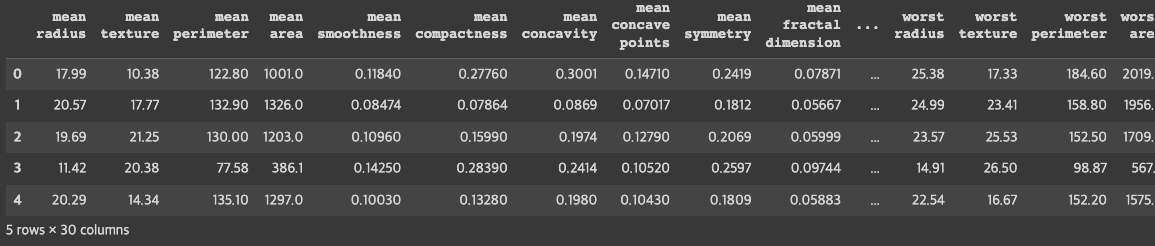

df['class'] = cancer.target
sns.pairplot(df[['class'] + list(df.columns[:10])])
plt.show()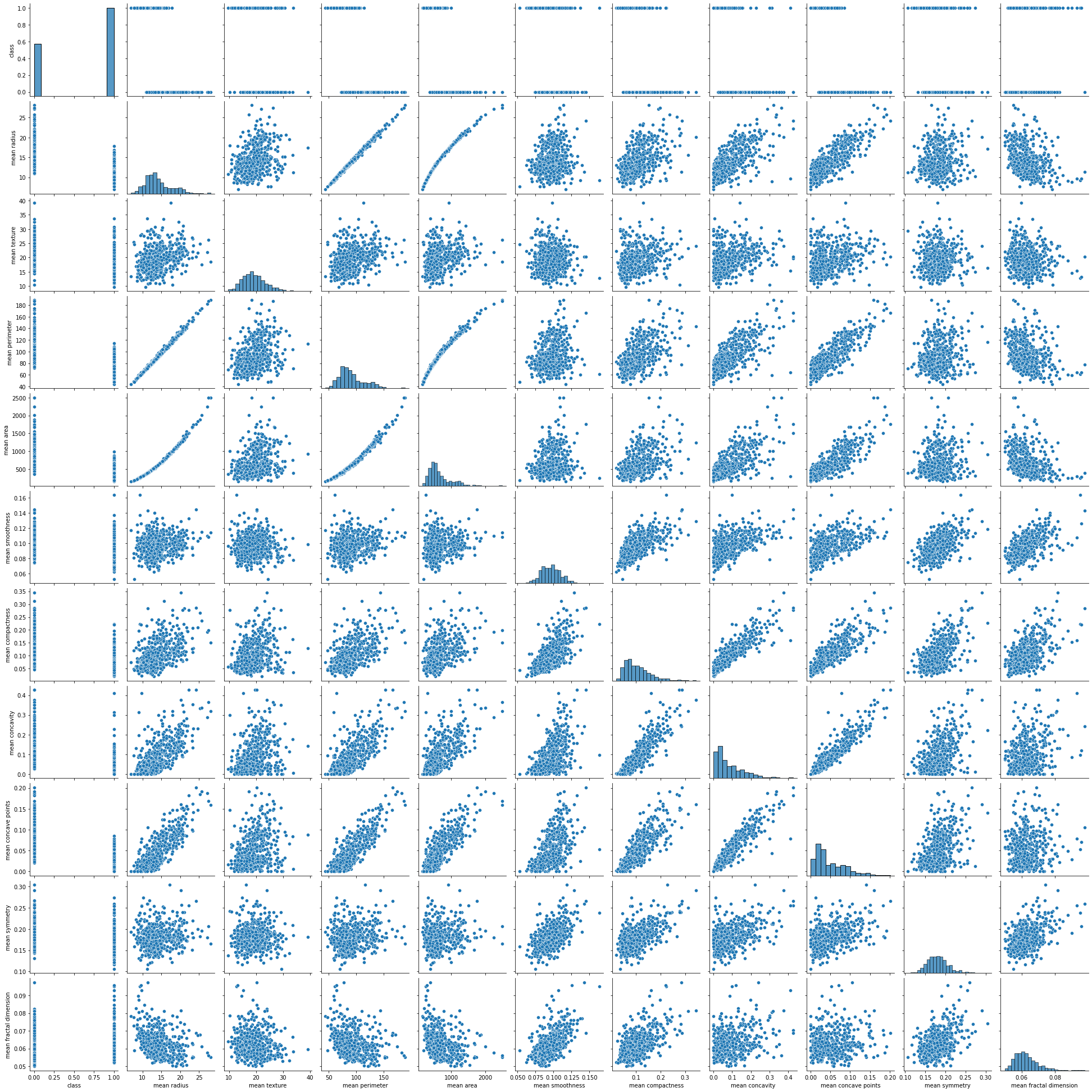

로지스틱 회귀모델 학습

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

data = torch.from_numpy(df[cols].values).float()

data.shape
# torch.Size([569, 8])

x = data[:, :-1]
y = data[:, -1:] # 정답 값
print(x.shpae, y.shape)
#torch.Size([569, 7]) torch.Size([569, 1])

에폭, 학습률, 프린트 간격 지정

n_epochs = 200000
learning_rate = 1e-2
print_interval = 10000

model

# costum model
class MyModel(nn.Module):
    
    def __init__(self, input_dim, output_dim):
        self.input_dim = input_dim
        self.output_dim = output_dim

        super().__init__()

        self.linear = nn.Linear(input_dim, output_dim)
        self.act = nn.Sigmoid()

    def forward(self, x):
        y = self.act(self.linear(x))

        return y # 예측 값

model = MyModel(input_dim = x.size(-1), output_dim = y.size(-1))

crit = nn.BCELoss()

optimizer = optim.SGD(model.parameters(), lr = learning_rate)

for i in range(n_epochs):
    y_hat = model(x)
    loss = crit(y_hat, y)

    optimizer.zero_grad()
    loss.backward()

    optimizer.step()

    if (i + 1)% print_interval == 0:
        print('Epoch %d: loss = %.4f' %(i+1, loss))
'''
Epoch 10000: loss = 0.2918
Epoch 20000: loss = 0.2436
Epoch 30000: loss = 0.2147
Epoch 40000: loss = 0.1958
Epoch 50000: loss = 0.1826

...

Epoch 170000: loss = 0.1336
Epoch 180000: loss = 0.1321
Epoch 190000: loss = 0.1307
Epoch 200000: loss = 0.1294
'''

correct_cnt = (y==(y_hat>.5)).sum()
total_cnt = float(y.size(0))
print('Accuracy : %.4f'%(correct_cnt/total_cnt))
# Accuracy : 0.9473