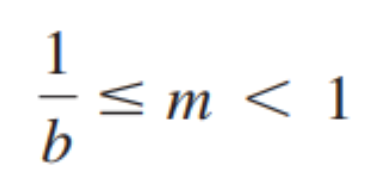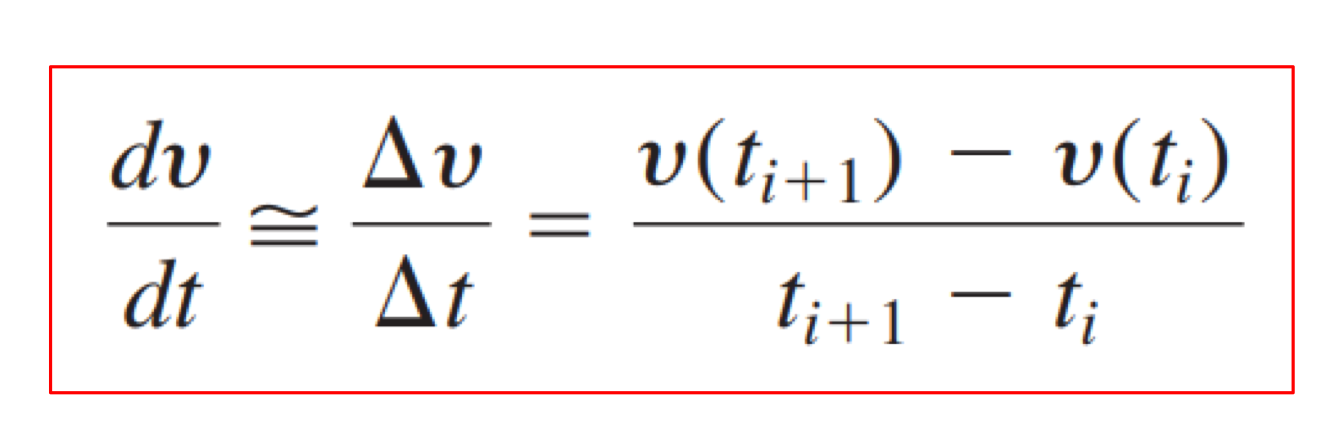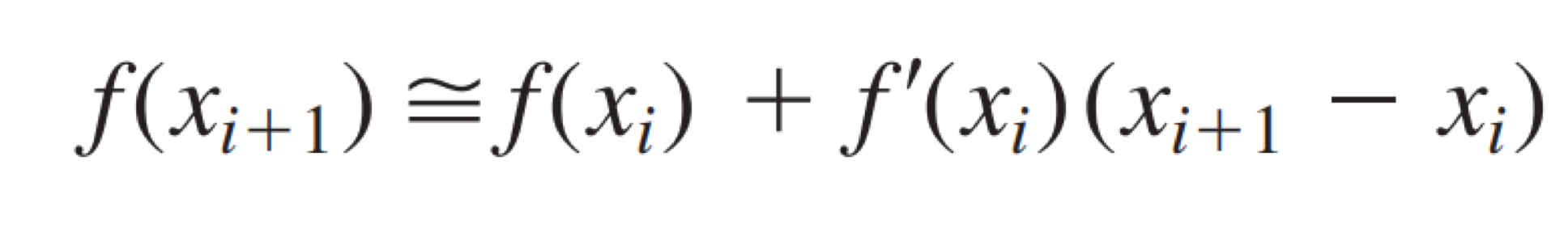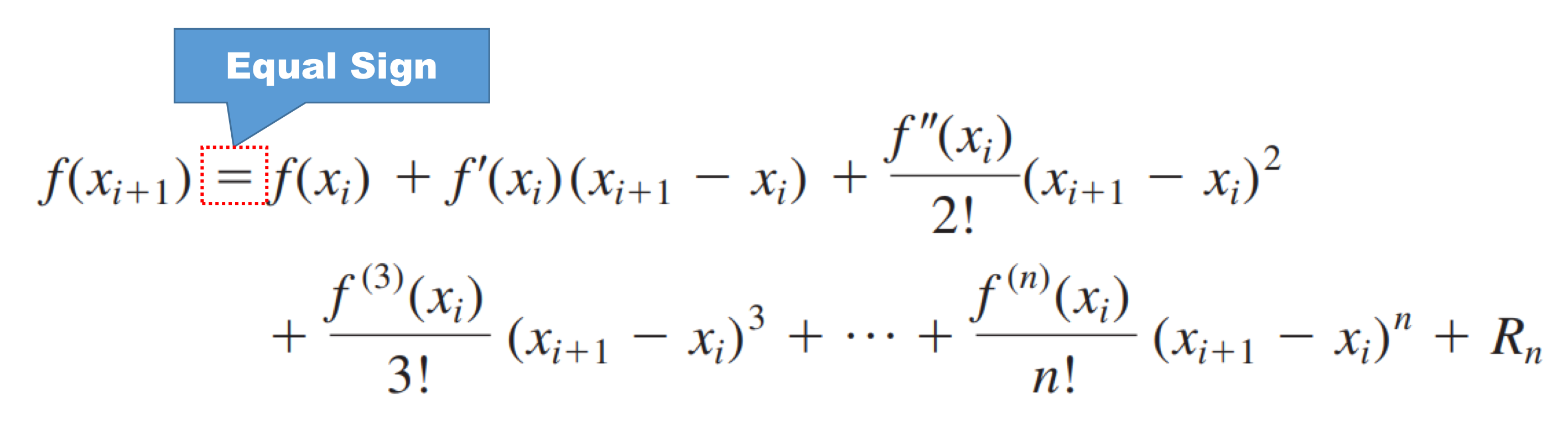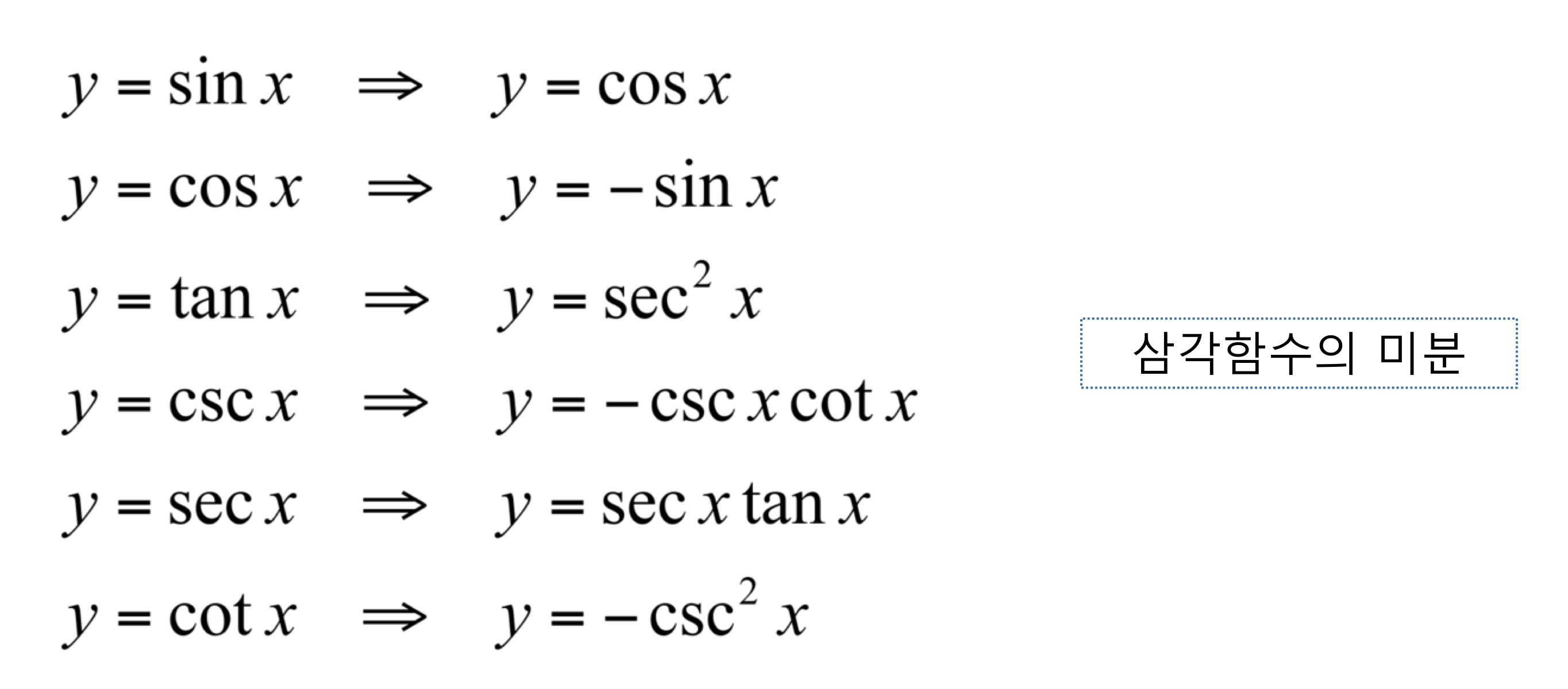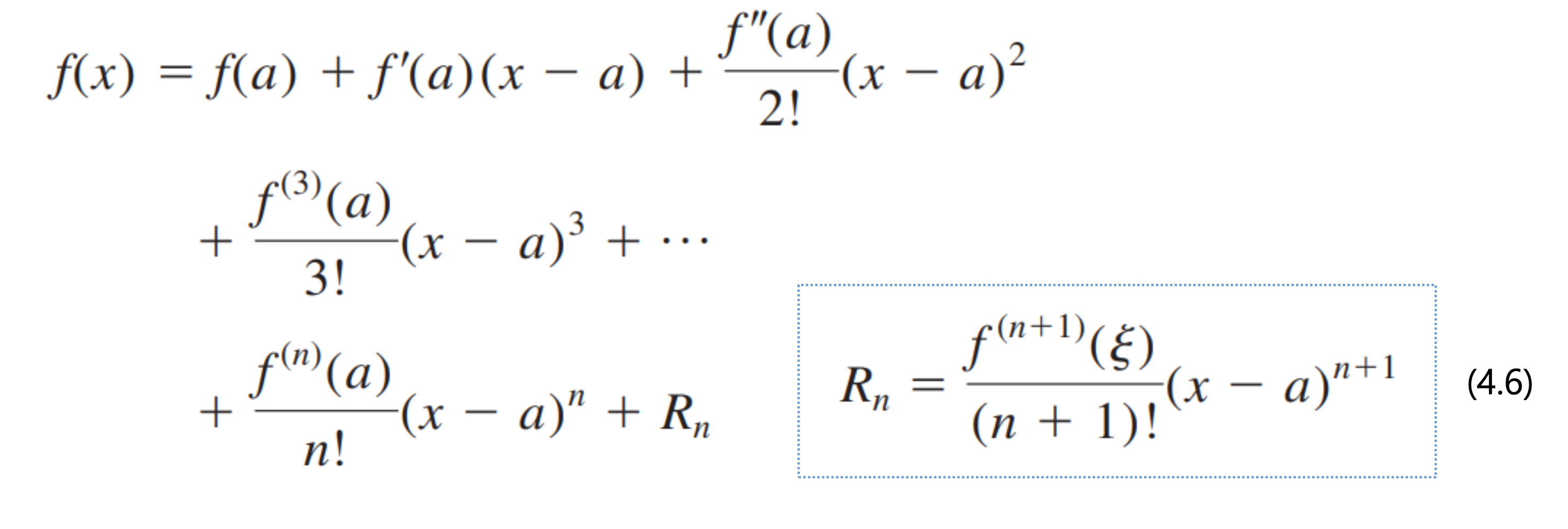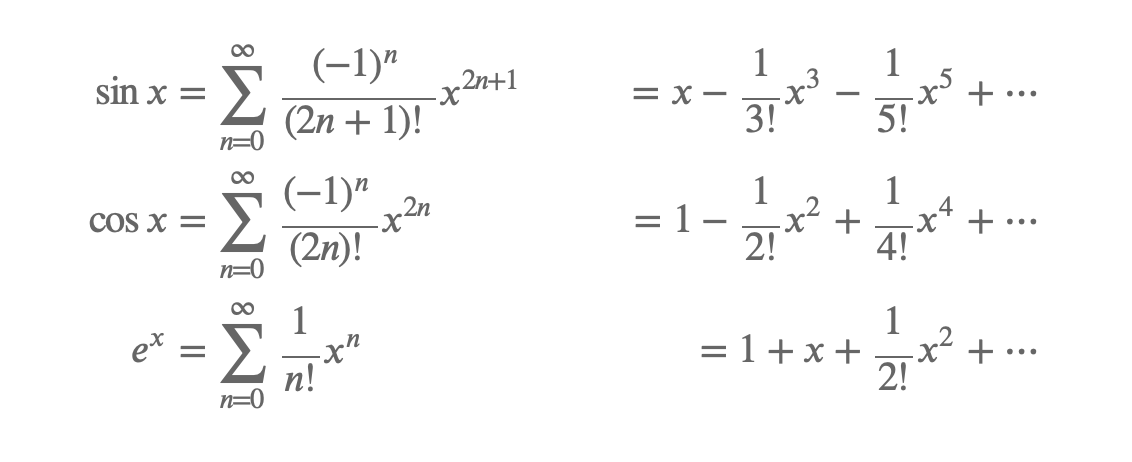Round-off Error
- 컴퓨터에서 숫자를 저장할때 32 혹은 64비트의 길이로 제한되어 정확하게 값을 저장하기 어려워 생기는 오차
정수
- 16비트로 정수를 표기할시 -32768 ~ 32767 사이의 숫자만 표현할수 있다.
실수
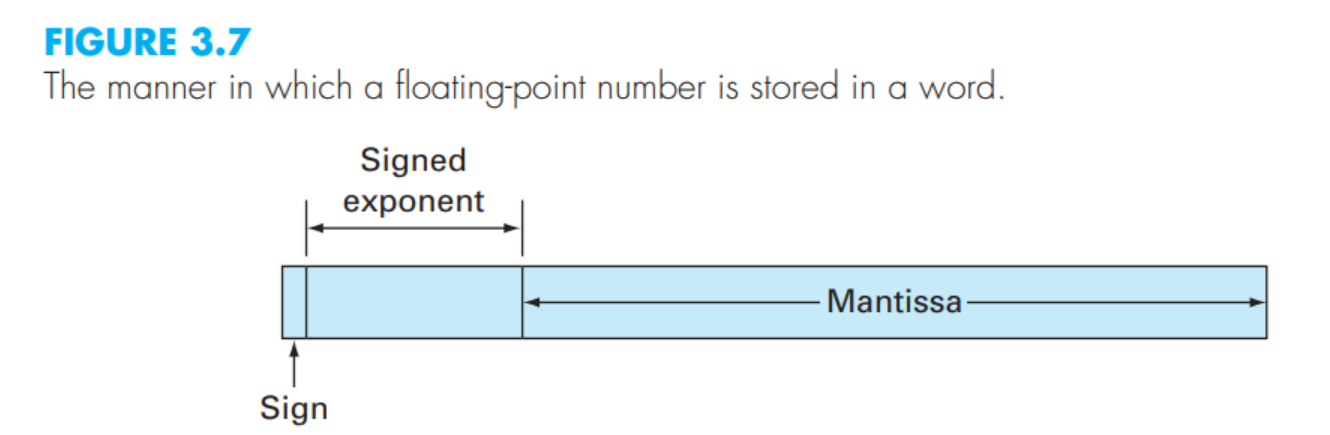
- 부호, 지수, 소수값 으로 구성된다.
- 소수를 정규화 한 뒤 위 값들로 저장한다.
실수의 오차

ϵ
- epsilon 으로 부른다.
- 1과 그 다음에 나올 수 있는 값의 차이를 이야기 한다.
- 1보다 일정수준 더 큰 숫자에 대해선 그 다음에 나올수 있는 값이 epsilon 의 2배가 된다.
- 계속 이 기조가 이어짐.

- epsilon을 구하는 방식, b는 진법이고 t는 mantissa에서의 유효숫자이다.
mantissa
- ieee754에서 소수부분을 표기하는 부분
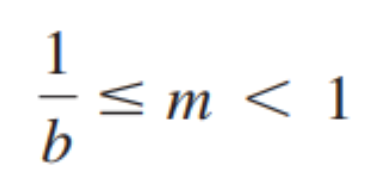
- 첫번째 자리수는 반드시 1이 되어야 한다.
- b : 진법
예시
- 4 다음에 나올수 있는 값의 차이는 1 다음에 나올수 있는 값의 차이의 두배가 된다.
오버플로우
언더플로우
실수의 덧셈

- 유효숫자가 4자리이기 떕문에 0.1600으로 잘린다.
- 이 외에도 여러번 연산을 해서 오차가 생길수 있다.

- 큰 실수와 작은 실수를 더할때에도 오차가 생긴다.
Truncation Error
- 수학적 계산을 할때 근사값을 이용하기에 생기는 오차.
예시
- 미분을 계산하기 위한 방법
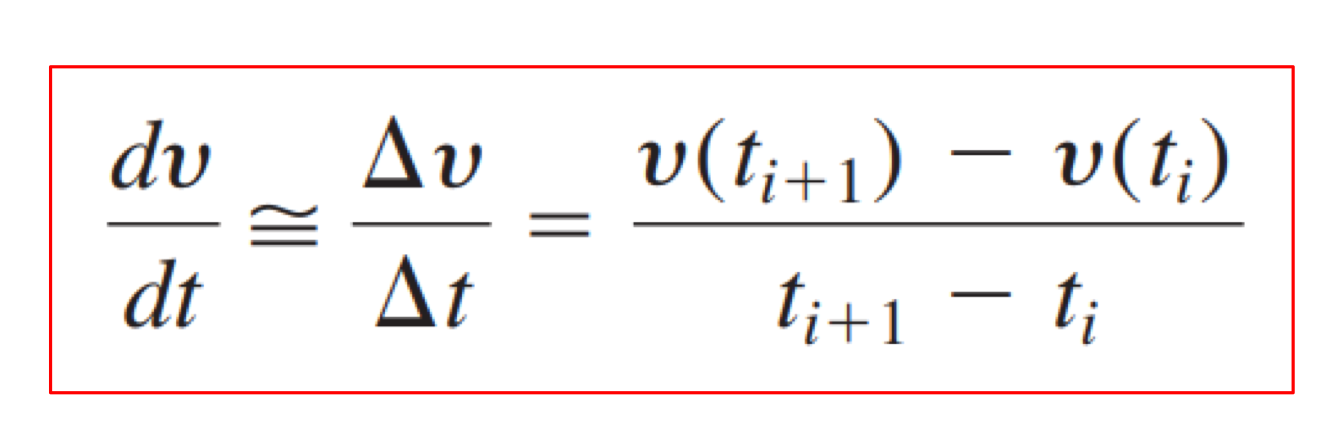
- 미분을 계산하기 위해 ( 그 접선의 기울기를 구하기 위해 ) 아주 짧은 구간의 기울기를 구한다.
- 실제 값이 아닌 근사값이다.
테일러 이론
- 어떤 함수를 임의의 값을 중심으로 값을 추정하기 위한 다항식으로 표현할수 있다.
- 다항식 : 테일러 급수 / Taylor series
- 다항식이 이어져 나갈수록 미분이 되기 때문에, 다항식의 길이는 미분 가능한 횟수에 의해 제한된다.
- 즉, 무한번 미분 가능한 경우 ( Ex. 삼각함수 ) 의 경우는 매우 완벽하게 표현이 가능해진다.

- f(a) 는 알고 있는 임의의 값, 이를 중심으로 다른 f(x)를 구하는 다항식을 만들어낸 모습이다.
- 미분 가능한 함수에서만 사용 가능하다.
미분 가능한 함수 == 부드러운 함수 == Smooth function
알려진 f(xi) 로부터 f(xi+1) 를 구하는 예시에서..
Zero-order approximation

- 이는 최초의 근사값을 의미한다. 해당 결과값이 필요할 때 매우 단순한 식을 구성하여 빨리 뽑아내는 것을 의미한다.
First-order approximation
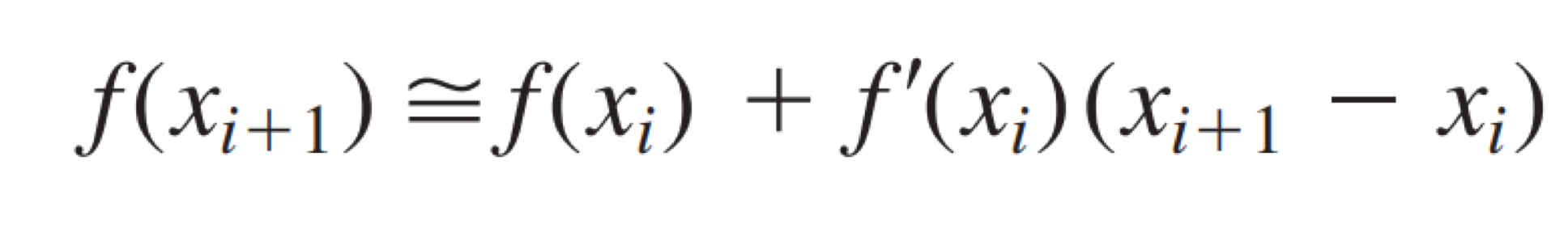
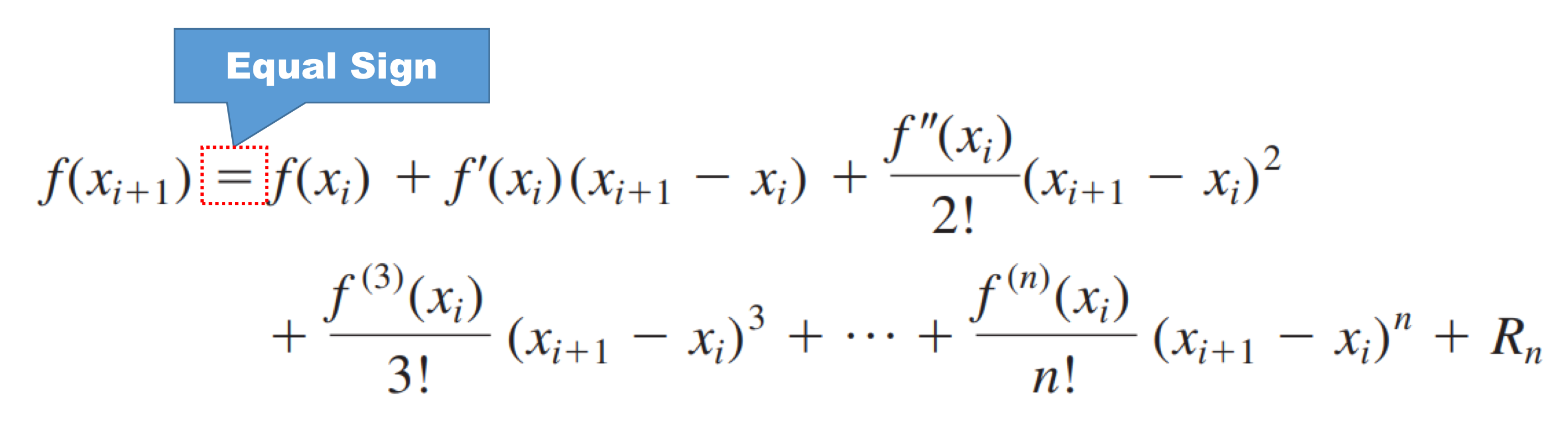
- 단 하나의 주요 수치를 발견하여 좀 더 발전된 식을 통해 값을 정의하는 것을 의미한다.
- f'(x_i) 는 x_i 에서의 기울기 ( 미분 값 )
이후

- 다항식에 항이 하나가 더 추가된 것.

- 생성된 테일러 급수 형태.
Step size
- xi+1−xi
- 새로 구하려는 위치와 이전 위치의 차이
- h로 표기
- 위 간격은 오차에 영향을 준다.

- 오차가 O(h) 이면 h를 절반으로 줄이면 오차가 절반
- 오차가 O(h^2)이면 h를 절반으로 줄이면 오차가 1/4

ex 와 테일러 급수의 예시
- n : approximation order ( 클수록 다항식이 더 길다. )


추가

연습문제1


- f(0) 의 값을 이용, f(1) 의 값을 근사하기 위한 과정이다.
연습문제2 - 삼각함수
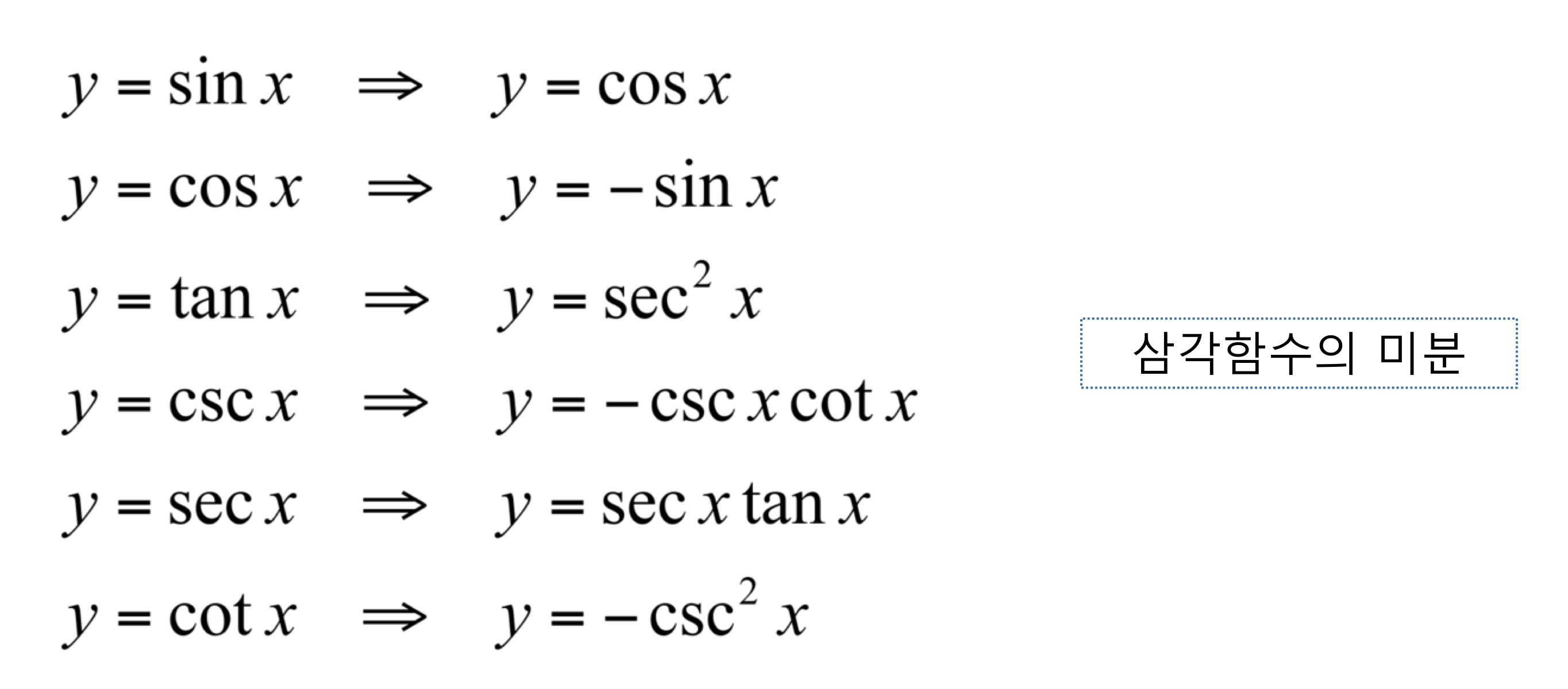
f(x)=cos(x) 이고 xi+1=π/3 이고 h=π/12 일때 계산

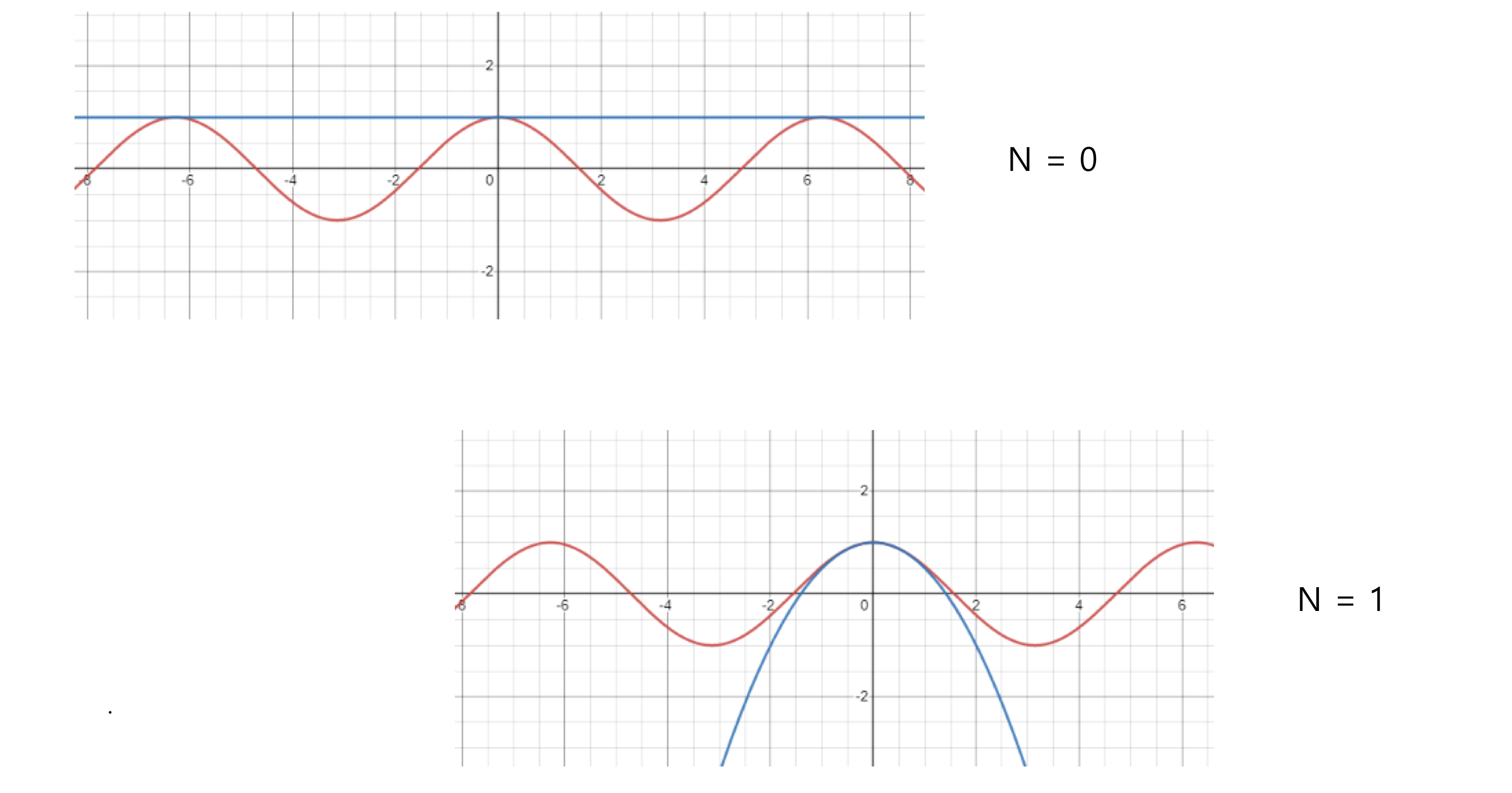

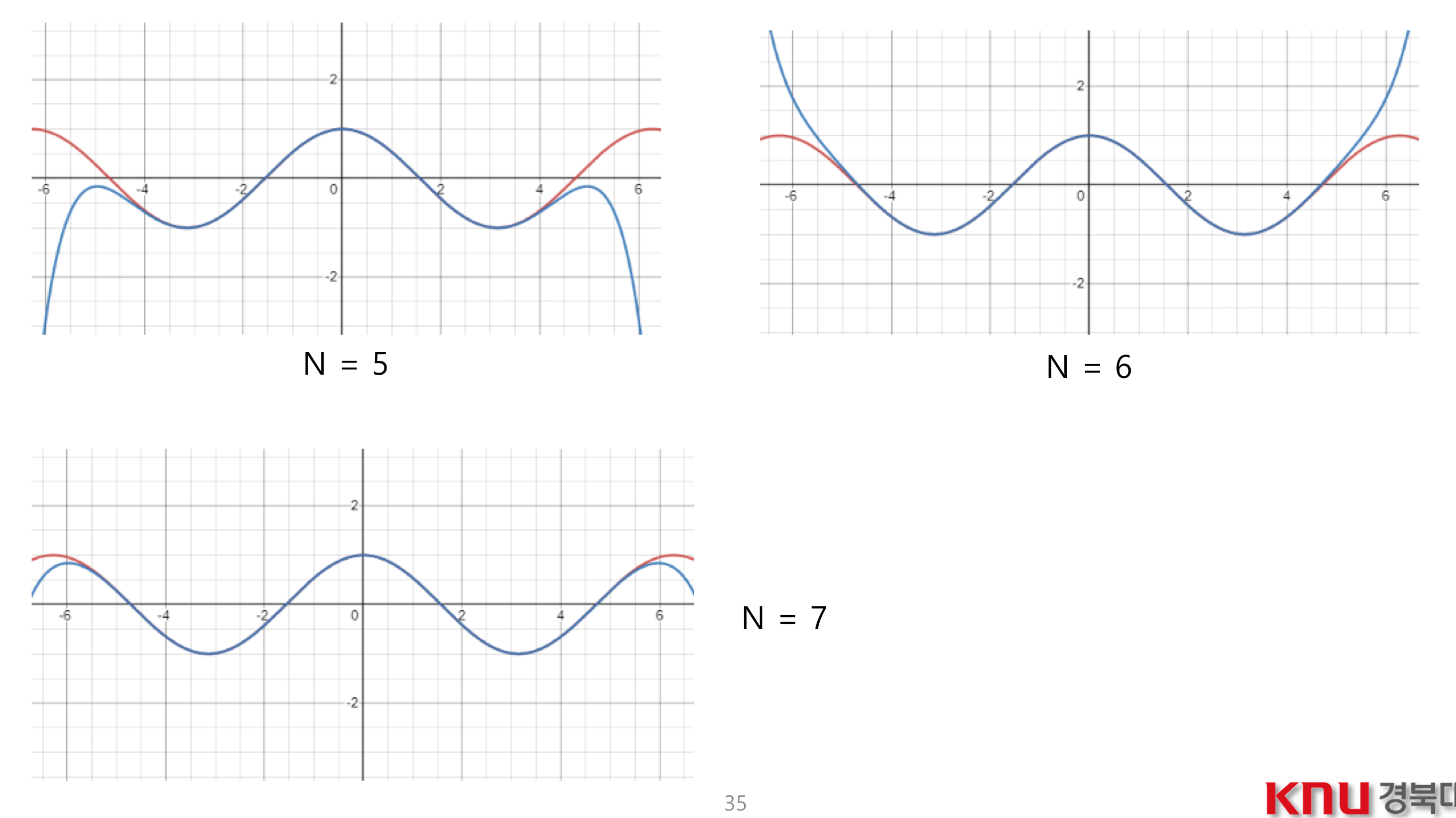
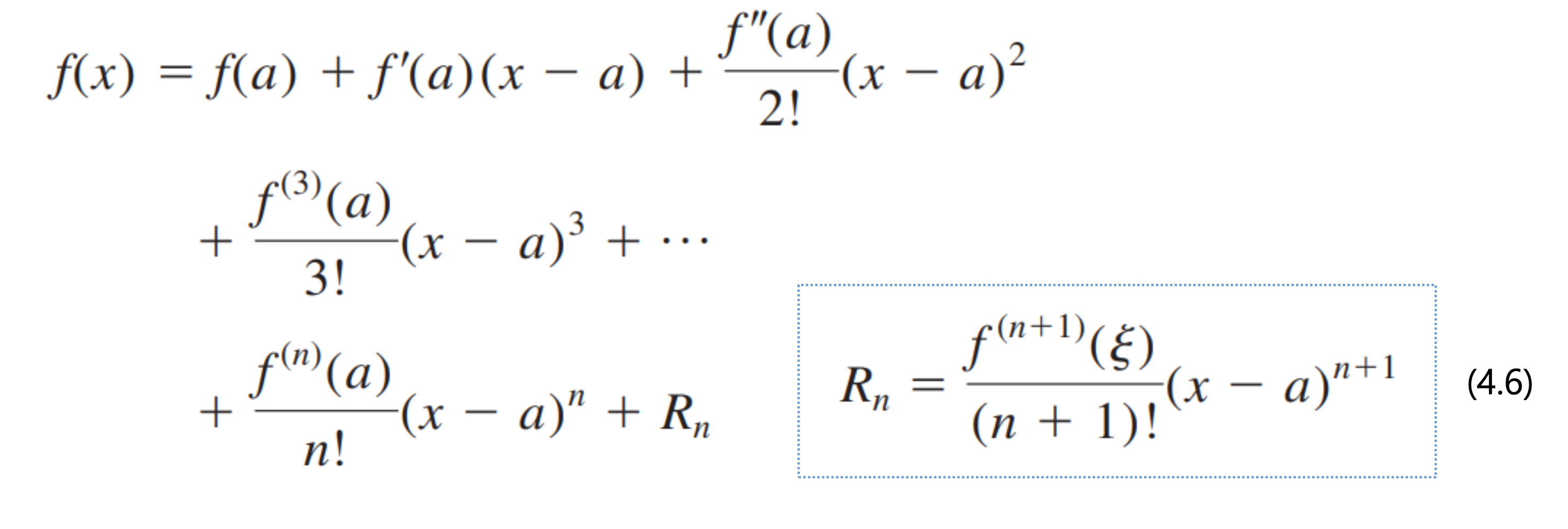
- 적당한 범위 내 까지 테일러 급수를 전개시, 근사값을 구한것이 되므로, 전개되지 않은 나머지 부분은 Truncation Error 가 된다.

- zero-order prediction 의 경우 Rn 의 예시
- 전개되지 않은 테일러 급수가 나머지 ( Rn ) 에 포함된다.
- ξ 는 xi 와 xi+1 사이의 특정 값.
미분의 평균값 정리

- 양 끝점의 기울기와 같은 기울기 값을 가지는 접선을 가지는 점이 양 끝점의 중간에 반드시 존재한다.
- 이 점을 ξ로 표기한다.
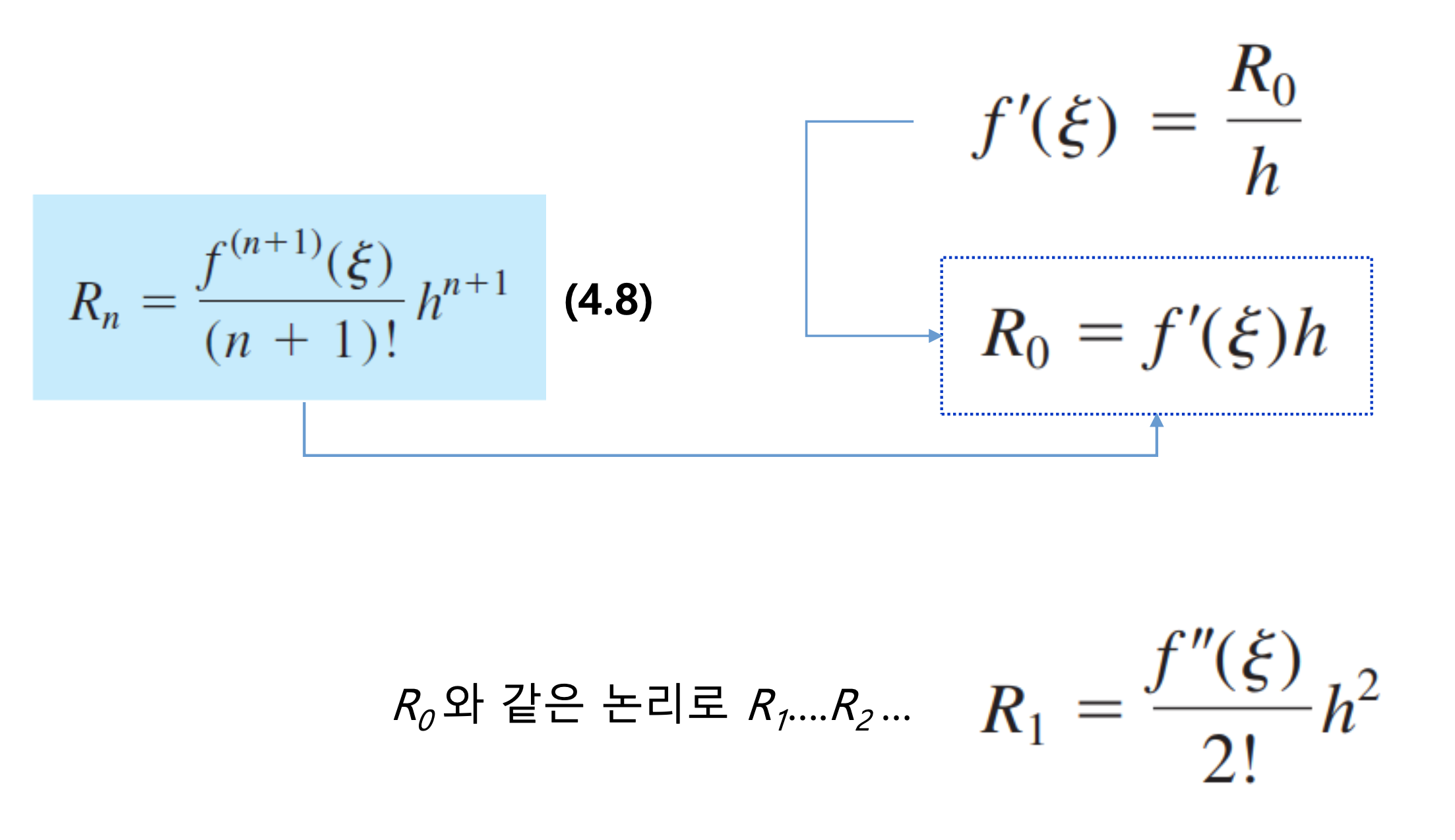
- 이를 통해 오차를 전개식이 아닌 단일 식으로 표현할수 있다.
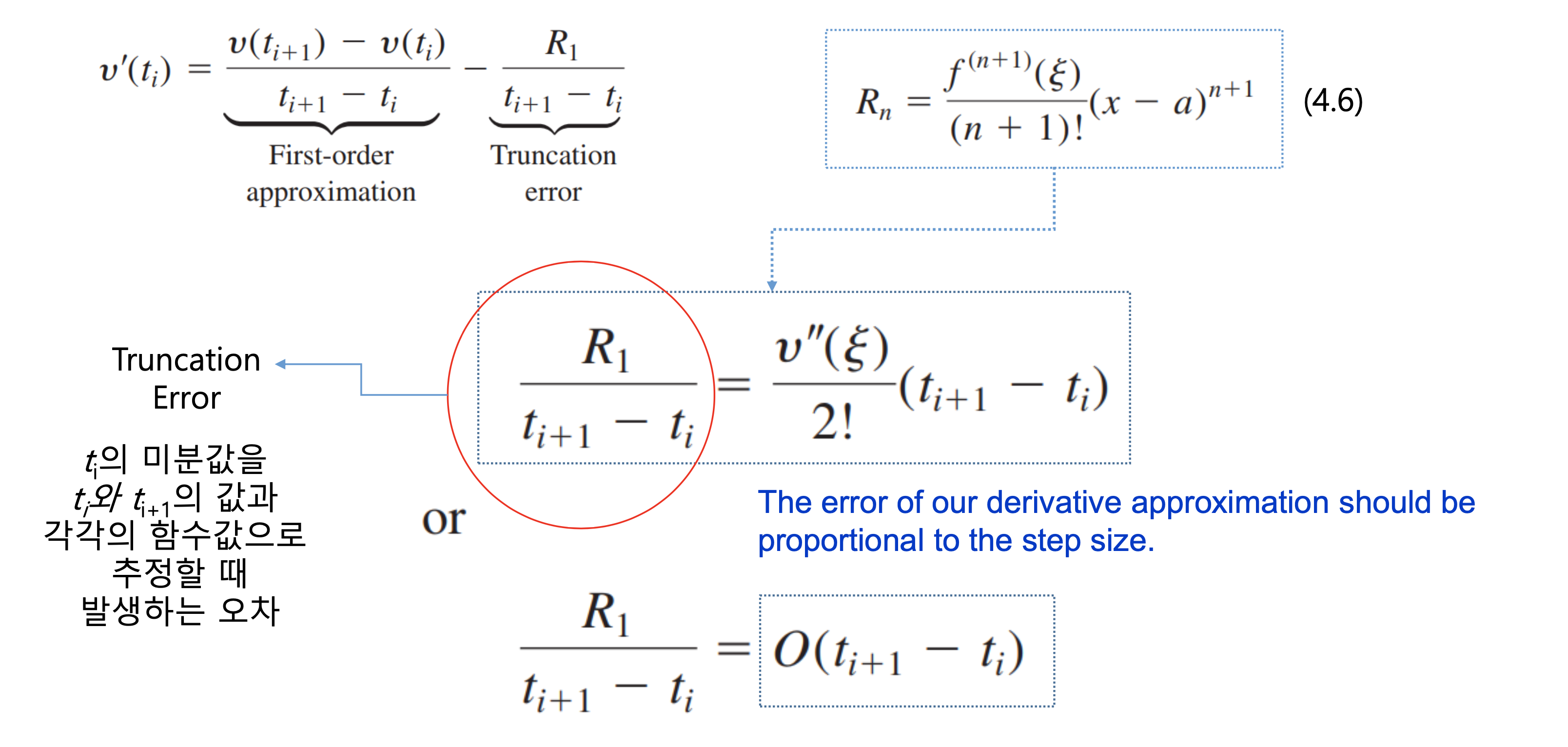
- 어떤 점에서의 미분값을 구할때, 그 점과 다음 점의 간격에 오차가 비례한다.
수치해석적 미분 계산방식
- xi 지점의 미분값을 구하려고 한다.
- 3가지 방식이 있다.

- xi−1 와 xi의 기울기를 구한다.
- first backward difference 로 부른다.
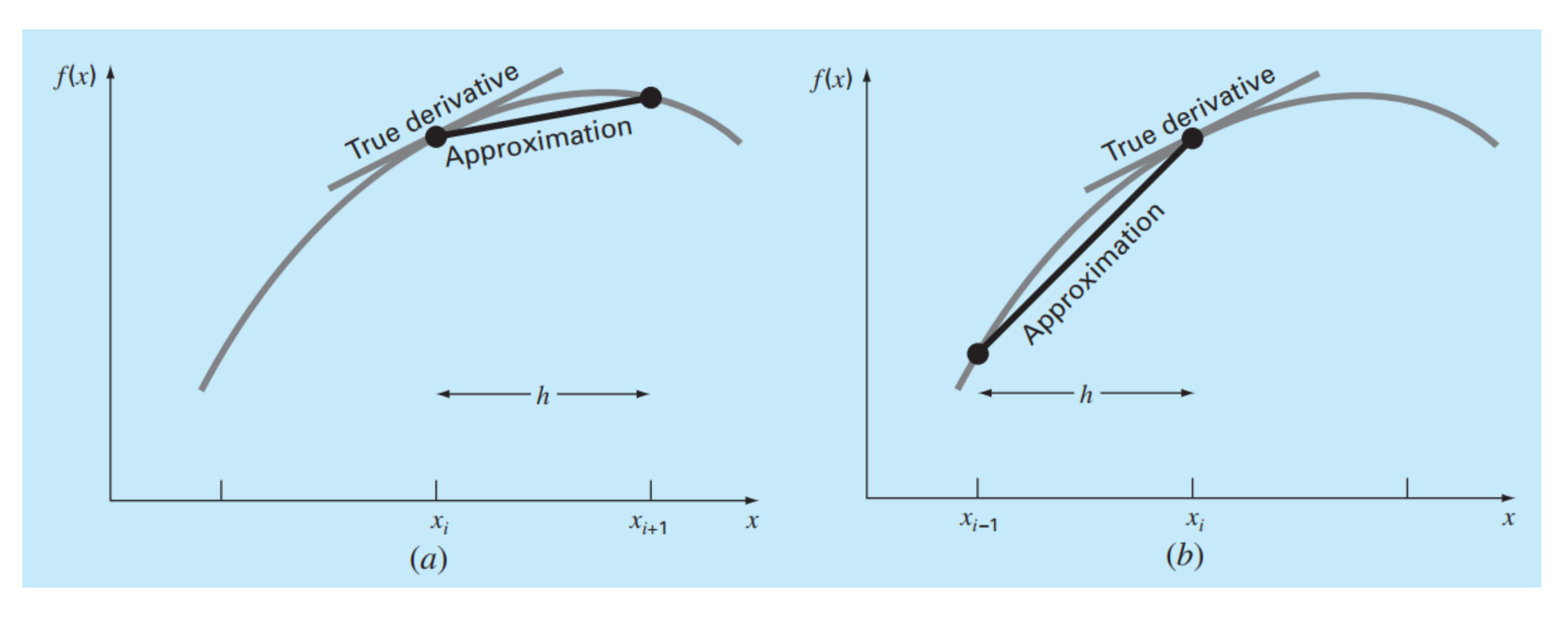
- xi 와 xi+1 과의 기울기로 구할수도 있다.
- 이 경우 first forward difference 로 부른다.
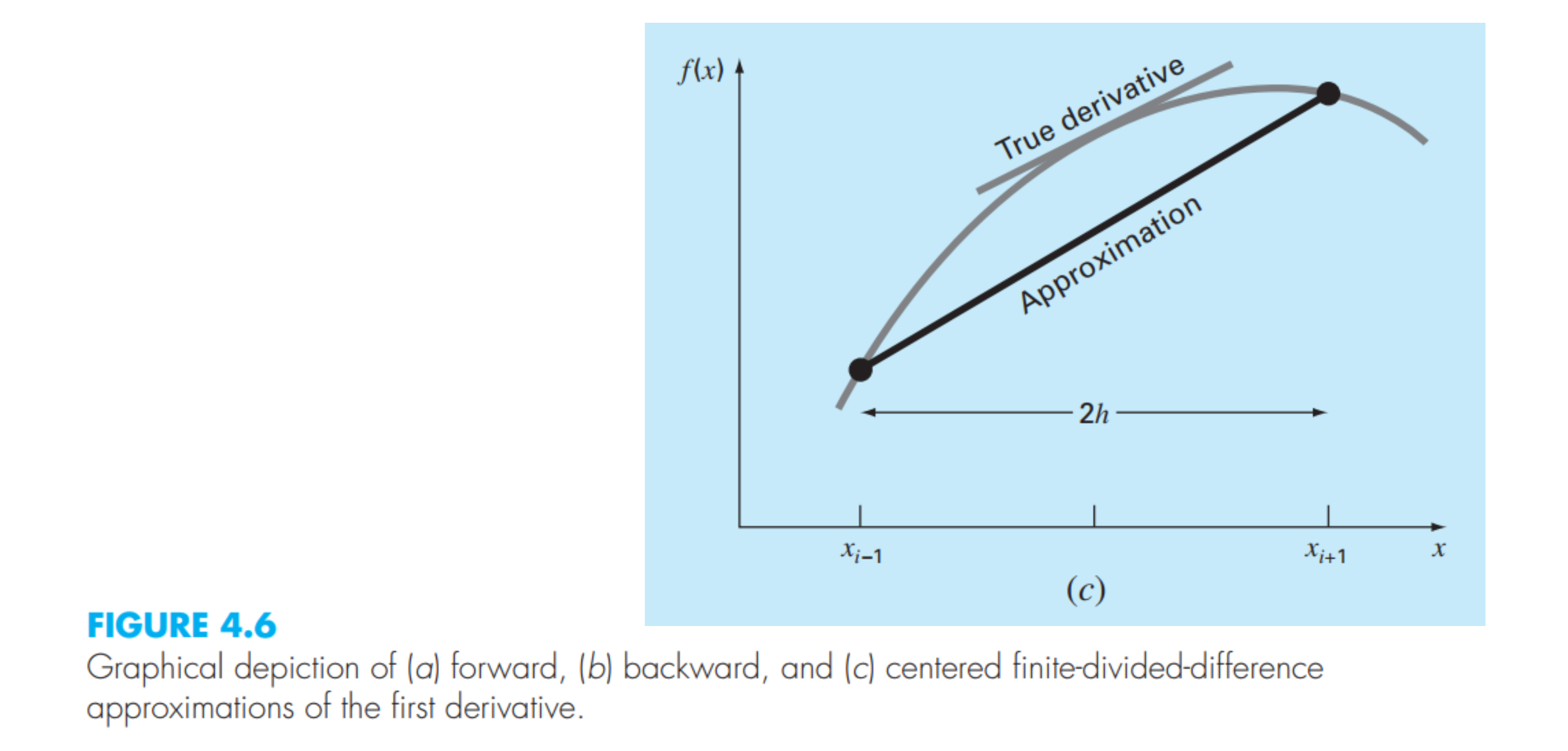
- xi−1 과 xi+1 의 기울기로 구할수도 있다.
- 이 경우 centered finite divided difference 로 부른다.
In Python..
- %precision {n}
- 주피터 노트북 환경에서 n자리 소숫점까지 표기하도록 한다.
- 다시 리셋하려면 %precision %r
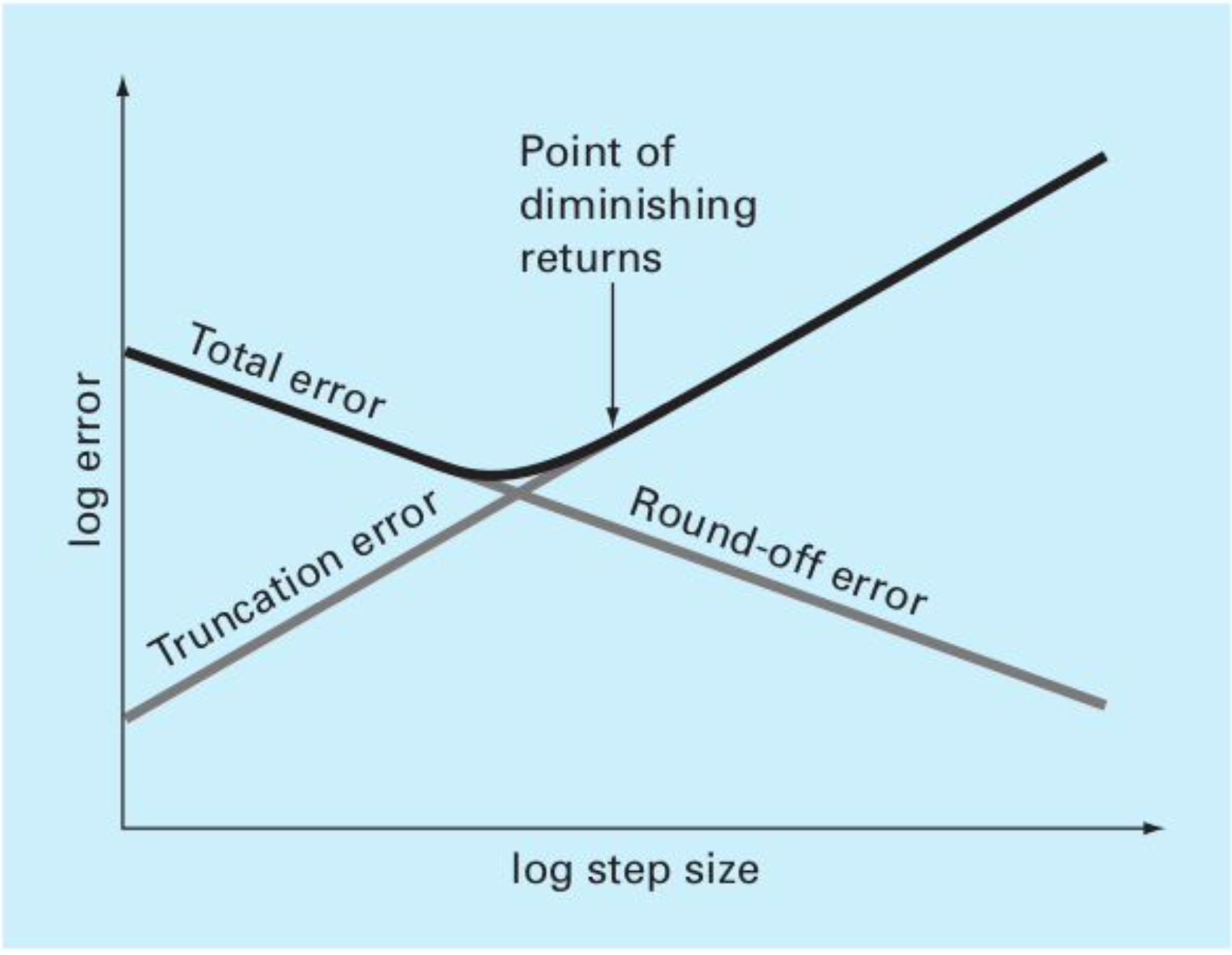
- truncation error 와 round-off error 의 합이 최소가 되는 지점을 찾아야 한다.

- 미분에서의 계산 예시
- 어느 지점까지는 step 이 줄어들수록 오차가 줄어들지만
- 어느 순간부터는 오히려 오차가 증가하는 모습을 보인다.
- 이는 step size를 표기하기 위한 자리가 부족해 점점 이상한 값이 되어가기 때문이다.
암기
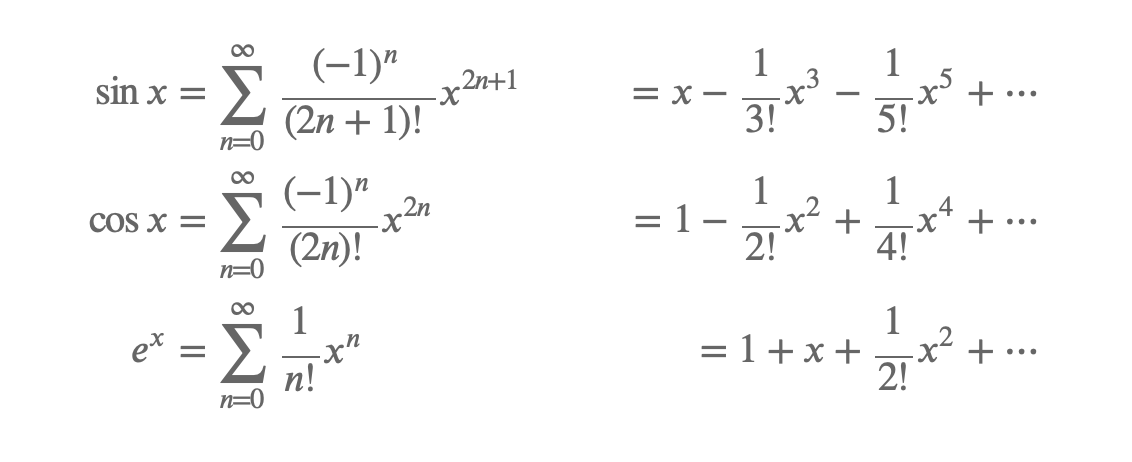
- 테일러 급수에서 a가 0이 될때를 기준으로 한다.