Leetcode 909. Snakes and Ladders

You are given an n x n integer matrix board where the cells are labeled from 1 to n2 in a Boustrophedon style starting from the bottom left of the board (i.e. board[n - 1][0]) and alternating direction each row.

You start on square 1 of the board. In each move, starting from square curr, do the following:

Choose a destination square next with a label in the range [curr + 1, min(curr + 6, n2)].
This choice simulates the result of a standard 6-sided die roll: i.e., there are always at most 6 destinations, regardless of the size of the board.
If next has a snake or ladder, you must move to the destination of that snake or ladder. Otherwise, you move to next.
The game ends when you reach the square n2.
A board square on row r and column c has a snake or ladder if board[r][c] != -1. The destination of that snake or ladder is board[r][c]. Squares 1 and n2 are not the starting points of any snake or ladder.

Note that you only take a snake or ladder at most once per dice roll. If the destination to a snake or ladder is the start of another snake or ladder, you do not follow the subsequent snake or ladder.

For example, suppose the board is [[-1,4],[-1,3]], and on the first move, your destination square is 2. You follow the ladder to square 3, but do not follow the subsequent ladder to 4.
Return the least number of dice rolls required to reach the square n2. If it is not possible to reach the square, return -1.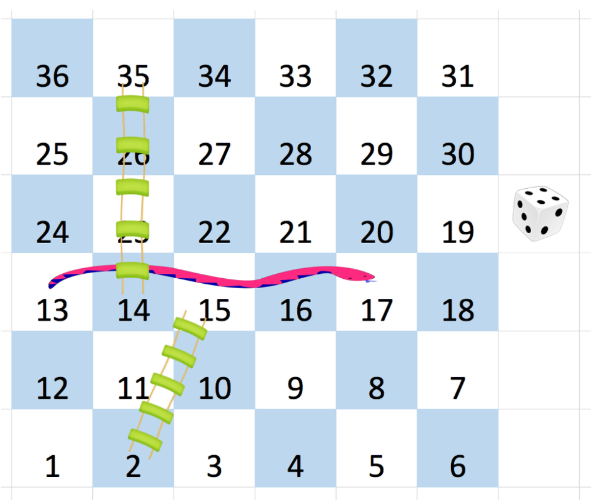

좌우교대서법 (Boustrophedon) 으로 만들어진 게임 판이 있고
해당 게임 판에 사다리 ( 더 높은 숫자로 이동 ) 와 뱀 ( 더 낮은 숫자로 이동 ) 이 있다.
N * N 게임판에서 1부터 시작할때, N * N - 1 위치에 도달해야 한다.
사용자는 1에서 시작해 1~6중 하나를 선택해 이동할수 있으며, 초과해서 도달 할 경우 맨 끝에서 멈춘다.
사다리나 뱀은 한 턴에 한번만 이동 가능하며, 이동 후 또 이동할수 있게 설치되어 있어도 멈춘다.
끝까지 도달하기 위해 최소한으로 필요한 이동 수를 구하라

풀이

class Solution:
    def snakesAndLadders(self, board: List[List[int]]) -> int:
        game = []

        N = len(board)
        END = N ** 2 - 1

        for row in range(N - 1, -1, -1):
            position = N - row

            if position % 2 == 1:
                game.extend(board[row])
            else:
                game.extend(board[row][::-1])

        game = [space - 1 if space != -1 else -1 for space in game]
        s = deque([(0, 0)])
        cache = [float('inf')] * (N * N)

        while s:
            position, count = s.popleft()

            for to in range(position + 1, min(position + 7, END + 1)):
                if game[to] != -1:
                    to = game[to]

                if cache[to] > count + 1:
                    cache[to] = count + 1
                    s.append((to, count + 1))

        return cache[-1] if cache[-1] != float('inf') else -1

• 먼저 너무 어지러운 게임판을 0-indexed 1차원 배열로 수정한다.
• 이후 BFS를 통해 가능한 경우의 수를 탐색한다.
• cache에는 cache[i] 에 i번째 칸에 올때 필요한 최소한의 이동 수를 계속 확인해 가면서 최적화한다.
• 만약 N * N - 1 번째에 도달하지 못했다면, -1 아니면 그 값을 리턴한다.