Prologue
Gradient descent가 발전해온 방향은 크게 두 가지가 있다. 첫 번째는 물리법칙을 따르는 방법. 두 번째는 학습을 거듭할수록 일정비율로 학습률을 줄여서 global minima를 지나가지 않게 하는 방법이다. 이번에 알아볼 것은 두 가지 방법을 섞어서 쓰는 알고리즘이다.
import numpy as np
import matplotlib.pyplot as plt
def f(x, y):
return 0.4*x**2*y**2 + 0.3*x**2*y + 0.3*x**2 + 0.3*y**2 - 0.25*x*y**2 + 0.31*x*y - 0.2*x + 2.1*y
def df(x, y):
dx = 0.8*x*y**2 + 0.6*y + 0.6*x - 0.5*y + 0.31*y - 0.2
dy = 0.8*x**2*y + 0.6*x**2 + 0.6*y - 0.5*x*y + 0.31*x + 2.1
return dx, dy
x = np.arange(-1, 2, 0.01)
y = np.arange(-2, 1, 0.01)
X, Y = np.meshgrid(x, f(x, y))
Z = np.sqrt(X**2 + Y**2)
plt.contour(X, Y, Z, 25, colors = ['gray'])
plt.plot(x, f(x, y))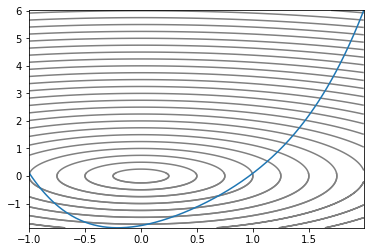
우리가 헤멜 Convex 지형이다. 2차원 2차함수에다 z축을 하나 추가해서 입체적으로 만들고 등고선처럼 높이가 같은 지점끼리 선으로 이었다. 가장 작은 원이 최소값을 갖는 지점이므로 optimizer가 저 원을 콕 찍으면 된다.
Adam
Momentum과 RMSProp을 합쳐놓은 알고리즘. 두 알고리즘이 잘 된다면 합쳐놓으면 더 잘 되지 않을까? 하는 인투이션이 들어있다. 섞어놔서 그런지 복잡하지만 어디 갖다놔도 잘 되서 흔히 쓰인다.
이 때 과 의 초기값으로 0.9 각각 0.999, 는 으로 정한다. 이러면 과 이 0이므로 첫 번째 스텝의 결괏값은 0으로 쏠리므로 과 을 아래와 같이 보정한다.
그래서 점의 이동은 이전의 알고리즘보다 좀더 복잡해진다.
조금 생각해보면 학습을 거듭할 수록 과 는 과 에 점점 가까워져서 결국에는 SGD와 생김새가 비슷해진다.
def adam(x, y, cache: dict, beta1 = 0.9, beta2 = 0.999, lr= 5e-2):
t = 0
dx, dy = df(x, y)
if len(cache['m']['x']) == 0 and len(cache['v']['y']) == 0:
mx = (1 - beta1) * dx
my = (1 - beta1) * dy
vx = (1 - beta2) * np.square(dx)
vy = (1 - beta2) * np.square(dy)
else:
mx = beta1 * cache['m']['x'][-1] + (1 - beta1) * dx
my = beta1 * cache['m']['y'][-1] + (1 - beta1) * dy
vx = beta2 * cache['v']['x'][-1] + (1 - beta2) * np.square(dx)
vy = beta2 * cache['v']['y'][-1] + (1 - beta2) * np.square(dy)
t += 1
cache['m']['x'].append(mx)
cache['m']['y'].append(my)
cache['v']['x'].append(vx)
cache['v']['y'].append(vy)
hat_mx = mx / (1 - beta1**t)
hat_my = my / (1 - beta1**t)
hat_vx = vx / (1 - beta2**t)
hat_vy = vy / (1 - beta2**t)
x = x - lr * hat_mx / (np.sqrt(hat_vx)- 1e-8)
y = y - lr * hat_my / (np.sqrt(hat_vy)- 1e-8)
return x, y
cache = {'v':{'x':[], 'y':[]}, 'm':{'x':[], 'y':[]}}
adamX, adamY = [.5], [5.8]
x, y = adam(*adamX, *adamY, cache)
adamX.append(x)
adamY.append(y)
for i in range(92):
x, y = adam(x, y, cache)
adamX.append(x)
adamY.append(y)
plt.contour(X, Y, Z, 25, colors= ['gray'])
plt.plot(adamX, adamY)
plt.title('Adam')
plt.xlabel('lr=5e-2, epochs=92')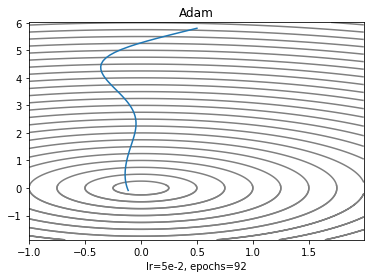
두 가지 특성을 섞어놔서 그런가 이 과제에서 기본 세팅으로는 SGD보다 수렴이 더 어려웠고 알고리즘이 높은 학습률을 요구하는 것처럼 보인다.
Epilogue
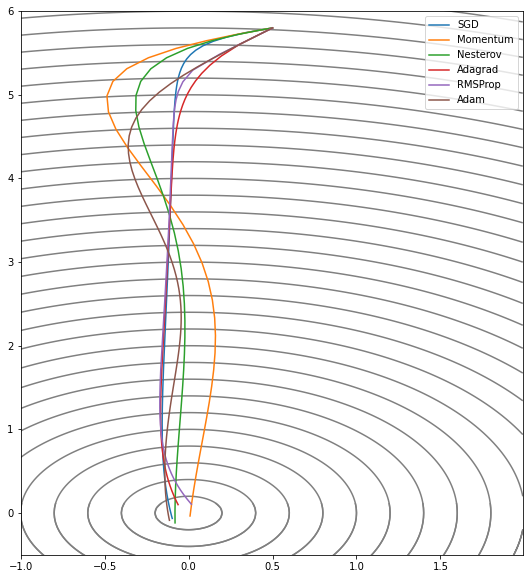
- 알고리즘에 많은 영향을 미치는 건 학습률과 epochs 두 가지.
- 웬만하면 Adam과 RMSProp을 먼저 시도해볼 것.
지금까지 2차원에서 minima를 찾아가는 과제에서도 각 알고리즘들의 개성을 엿볼 수 있다. MNIST만 하더라도 FCL로 풀어내려면 784차원이고 우리가 일반적으로 다뤄야 하는 과제는 적어도 수천만, 수억개의 차원을 가진 모델들이라 minima를 찾아가는 과제는 이렇게 단순하지는 않다.