Prologue

한국어로 경사하강법. gradient descent를 처음 들었을 때 딱 이런 느낌이었다. 어딘가에서 조금씩 내려간다고.
어떤 함수의 최소값을 찾아주는 알고리즘이다. 반대 개념은 descent 대신 ascent. 오늘 우리가 할 것은 데이터의 경향성을 그리는 함수 와 그 경향성을 예측하는 함수 가 있을 때 와 을 적절히 업데이트하면서 모든 입력값 에 대해 가 되는 와 를 찾을 거다. 비용함수, 편미분을 들어봤다면 쉽게 이해할 수 있다. 간단하게 선형회귀 과제에서 흐름을 살펴보면 다른 과제에서 어떻게 돌아가는지 쉽게 알 수 있을 거다. 그러면 차근차근 구현하면서 알아보자.
Data preparation
# Creating arbiturary ground truth
def gt(x):
return x * random.randint(-5, 5) + random.randint(-5,5)
# Input value
x = np.random.randn(100, 1)
# Plotting
gt = gt(x)
plt.figure(figsize = (5,5))
plt.scatter(x, gt)
plt.title('Ground truth')
plt.show()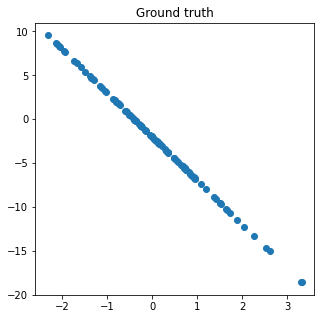
Initial model
# Initial weight and bias
params = {'w': random.randint(-10, 10), 'b': random.randint(-10, 10)}
print(params)>> {'w': 1, 'b': 2}def prd(x):
return params['w']*x + params['b']
p = prd(x)
plt.figure(figsize = (5,5))
plt.title('Predict')
plt.scatter(x, p)
plt.show()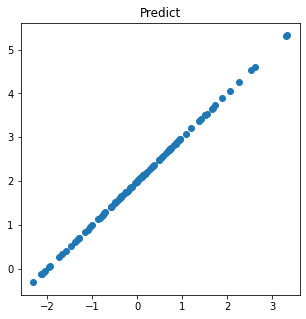
Cost/Loss function
모델이 예측한 그래프는 한 눈에 봐도 다르게 생겼지만 얼마나 정확한지 수치로 가늠할 건데 이것을 비용함수나 손실함수 혹은 목적함수라고 한다. 예측값과 실제값이 얼마나 다른가 직접적으로 비교하는데는 선형회귀 과제에서 이 차이들의 합은 언제나 0이라는 문제가 있다. 이것을 해결하는 방법은 두 가지.
- 제곱
- 절댓값
여기에서는 오차에다 제곱을 하기로 하고 평가지표로 오차제곱의 합(SSE: Sum of Squared Error)이나 오차제곱의 평균(MSE: Mean Squared Error)을 쓴다. 우리는 MSE를 써보자
위 식에서 입력값은 이미 알고 있으므로 우리는 weight와 bias를 점진적으로 업데이트하면서 MSE를 최소값을 갖도록 할거다.
def mse(gt, p):
return np.mean(np.square(gt - p))Gradient descent
위에서 구한 오차제곱에다가 평균을 구했더니 약 63언저리가 나왔다. 이 값을 최대한 줄여주는 parameter를 찾는 역할을 경사하강법이 하는데 알고리즘을 생각해보면
:
이렇게 된다. 위 식을 풀어보면
- 비용함수 를 번째 로 미분하고
- 1의 결과를 학습률 와 곱해서
- 번째 에서 2의 결과를 뺀다.
- 3의 결과를 번째 로 업데이트.
- 수렴할 때까지 1-4 반복.
이 되겠다. 알고리즘이 시키는대로 해보면 우리가 필요한 것은 비용함수에 대한 parameter의 미분값과 학습률이다. 앞서 우리는 parameter로 가중치와 편향 2가지를 각각 구할 거라서 편미분을 할 거다.
편미분?
개인적으로 영어표현이(Partial derivative) 좀더 직관적으로 다가온다. 미분이긴 한데 한 쪽으로 쏠렸다고. 간단하다. 이라는 다항식이 있다고 치자. 이 때 (함수 를 로 미분한 값)이 필요하다면 말고 나머지 변수는 상수처럼 생각하고 에 대해서만 미분하는 것을 편미분이라고 한다.
def derivative(func, x):
h = 1e-5 # super small value
return (func(x+h)-func(x)) / h # calculus equation
func_w = lambda w: (gt - (w * x + params['b']))**2 # df/dw
func_b = lambda b: (gt - (params['w'] * x + b))**2 # df/db
w = derivative(func_w, params['w'])
b = derivative(func_b, params['b'])
print('gradient of weight: {} \ngradient of bias: {}'.format(np.mean(w), np.mean(b)))>> gradient of weight: 17.611383794663617
>> gradient of bias: 8.898585332539858Put it together
이제 이걸 다 합하면 loss가 0에 수렴할 때까지 알고리즘이 돌아갈 거다.
lr = 1e-3
epochs = 2500
'''
parameter를 업데이트하면서 loss가 어떻게 변하는지 관잘할 거다.
loss, weight, bias, 그리고 weight와 bias 각각의 gradient도 기록해둔다.
'''
loss = {}
weight, bias = {}, {}
gradient_w, gradient_b = {}, {}
for epoch in range(epochs):
p = prd(x)
l = mse(gt, p)
loss[str(epoch+1)] = l
w = derivative(func_w, params['w'])
gradient_w[str(epoch)] = np.mean(w)
params['w'] -= lr * np.mean(w)
weight[str(epoch)] = params['w']
b = derivative(func_b, params['b'])
gradient_b[str(epoch)] = np.mean(b)
params['b'] -= lr * np.mean(b)
bias[str(epoch)] = params['b']
if epoch % 100 == 1:
print('epoch: {} ================================================='.format(epoch+1))
print('Loss: {} Weight: {} Bias: {}\n'.format(loss[str(epoch+1)], params['w'], params['b'])).
.
epoch: 902 =================================================
Loss: 0.594492686529058 Weight: -4.593833848948833 Bias: -1.4316118027285363
epoch: 1002 =================================================
Loss: 0.36133411719756414 Weight: -4.700900568006031 Bias: -1.5394604256348476
epoch: 1102 =================================================
Loss: 0.22134088865379284 Weight: -4.780239371478747 Bias: -1.626492872815358
epoch: 1202 =================================================
Loss: 0.13666109551253053 Weight: -4.838947309183286 Bias: -1.696809958573855
epoch: 1302 =================================================
Loss: 0.08504431601139308 Weight: -4.882319384645248 Bias: -1.7536854159338526
epoch: 1402 =================================================
Loss: 0.05333305576535899 Weight: -4.914303596530063 Bias: -1.799737065512967
.
.직관적으로 와닿게 그래프로 한번 더 보자.
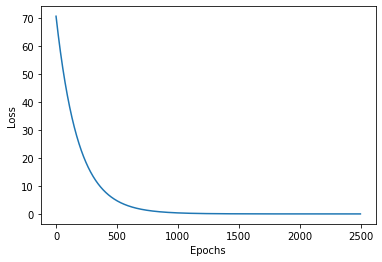
학습 후에 parameter와 어떻게 예측하는지 보자.
{'w': -4.998546908914805, 'b': -1.9785739972160354}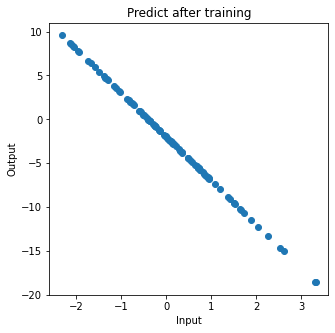
기가 막힌다. 학습 후의 그래프가 실제 값에 가까워졌다. 이제 학습을 진행할수록 parameter가 어떻게 바뀌는지 시각적으로 보자.
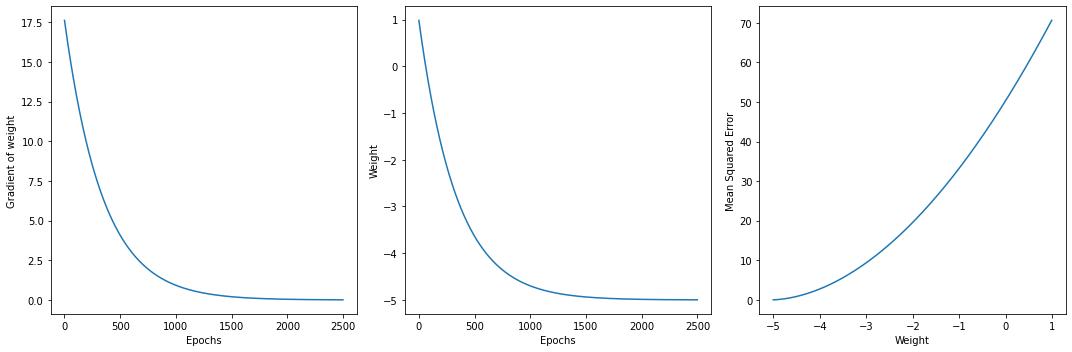
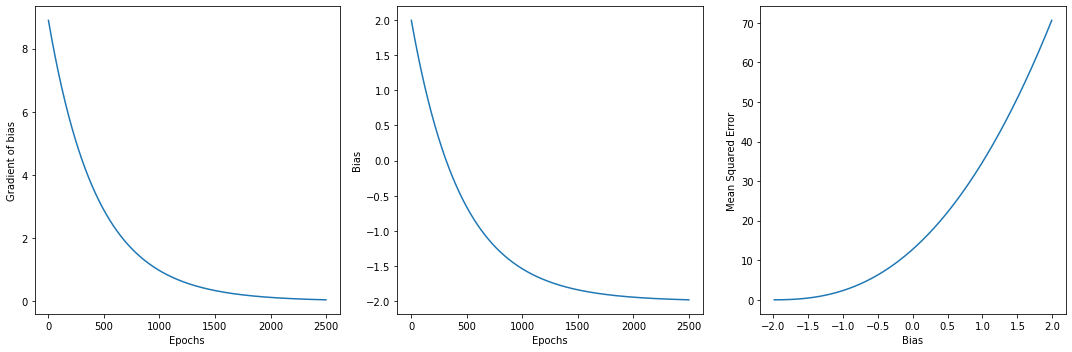
그래프에서도 보이다시피 학습을 진행할수록 parameter의 기울기가 수평에 가까워지고 특정값을 향해 수렴한다. 동시에 Loss값도 낮아진다.
Epilogue
사실 처음에 경사하강법을 이렇게 배웠다.
선형회귀의 비용함수로 MSE를 언급하고 그래프로 convex를 그린다. 그래프 위에 임의의 점을 찍은 다음 접선을 그리고 미분을 통해 접선의 기울기를 구한다. 학습을 거듭하면서 parameter에서 기울기의 학습률만큼 빼거나 더해서 오차제곱합이 최소가 되는 parameter를 찾으면 그래프의 극점이 된다. 그 지점에서 오차제곱이 최소가 되는 가중치와 편향을 구할 수 있다.
비용함수가 그냥 2차 함수라서 '그렇구나' 하고 받아들였지만, 이번에 구현하면서 중간중간 빠진 논리들을 채우느라 시간을 좀 들였다. 역시 잘 모르면 구현에서 막힌다. 내가 궁금했던 것을 나열해보면
- 극점 찾기에는 절댓값이 편한 거 같은데 왜 안 쓰나?
A. parameter를 조금씩 바꾸려면 미분이 필요하다. 미분이 들어가는 과제에서는 절댓값을 썼을 때 문제점이 크게 두 가지가 있다. 먼저 함수에 따라 구간을 나누어 줘야 극한 값을 찾을 수 있는 경우가 있다. 같은 맥락인데 미분값은 연속하는 구간에서만 구할 수 있다. 즉 절댓값 그래프처럼 꺾은선의 꼭지점에서 미분값을 구하려면 구간을 나눠야 해서 프로그램을 만들 때 연산량도 좀더 들고 코드문도 길어질 것 같다.
-
비용함수가 2차함수가 된다는 점은 감각적으로 알겠는데 x축이 어떤 값인지 모르겠다.
A. 함수 를 생각해보면이므로 x축에는 예측값이 들어가야 한다.
def cost(gt, p):
return np.square(gt - p)
l = cost(gt, p)
plt.figure(figsize = (5, 5))
plt.scatter(p, l)
plt.title('Cost function')
plt.xlabel('Predicted value')
plt.ylabel('Squared error')
plt.show()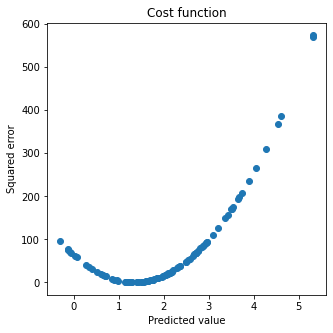
처음엔 이런 건줄 알았다.
- 엄밀히 따지자면 2에서 구한 비용함수 상에서 초기값으로 설정한 가중치와 편향에 해당하는 접선을 못 긋겠다. 이 함수에서 극점을 찾아가는 과제가 맞나?
A. 마지막 6개짜리 그래프 중 각 줄의 3번째 그래프를 보자. 둘 다 70 언저리에서 0까지 Loss 값이 떨어지는 것을 관찰할 수 있다. 비용함수 위에서 극점을 찾아가는 과제처럼 보이지만 70언저리로 보이는 값은 초반에 나왔던 오차제곱의 평균이다. 마지막 그래프들은 학습을 거듭하면서 지표들을 관찰했더니 convex function이더라 이렇게 받아들여야 할 것 같다. convex optimization을 찾아봐야 하나 싶다.
- 가중치와 편향을 업데이트 할 때마다 비용함수의 모양과 위치가 바뀔 텐데 그러면 같은 그래프상에서 3번을 생각할 수 없을 것 같은데?
A. 처음에 2번 그래프에서 한 점을 찍어서 왔다갔다 하는 줄 알았더니 그게 아니었다.
지금까지 경사하강법에 대해 알아봤다. 여기에서는 가중치와 편향을 scalar로 구현했는데 행렬로 바꾸면 신경망 모델에서 작동하는 back prop을 구현할 수 있을 것 같다. 경사하강법을 구현하면서 느낌적 느낌으로만 받아들이던 것들을 눈으로 직접 보는 느낌이었다. 심증으로 추정하던 대상의 물증을 찾은 느낌이랄까.