쉽게 배우는 자료구조 with 파이썬에서 배운 내용을 정리한 포스트입니다.

🧩 색인

1부터 10까지 적힌 10개의 카드가 있다. 이 카드들이 무작위로 섞인 채 뒤집혀있다면 원하는 숫자를 찾을 때까지 하나하나 확인해 봐야 한다. 그래도 다행히 카드가 10개 밖에 없기 때문에 운이 나빠도 10번만에 원하는 숫자가 적힌 카드를 손에 넣을 것이다.

그러나 카드의 개수가 100개, 1000개, 10000개 까지 늘어난다면 하나하나 확인하기에는 너무 오래걸린다. 데이터를 카드에 빗대어 생각해보면 엄청나게 많은 데이터가 축적되어있는 데이터베이스에서 원하는 데이터를 찾아내는 일은 자료구조와 알고리즘의 핵심 역할 중 하나다. 이때 나중에 데이터를 잘 찾을 수 있도록 색인을 만드는 작업이 중요하다.

배열에 키를 정렬시키는 것이 가장 생각하기 쉬운 자료구조다. 만약 카드가 정렬되어 있었다면 원하는 카드를 찾는 시간은 평균 O(LogN) 밖에 걸리지 않았을 것이다. 하지만 배열은 삽입과 삭제 시 평균 O(N) 의 시간이 소요되는 큰 단점을 가지고 있다.
이진 검색 트리는 이보다 개선된 저장 방법으로 검색, 삽입, 삭제 연산에 평균 O(LogN)의 시간이 소요된다. 물론 운이 나쁘면 아주 비효율적일 수도 있다.

🧩 검색 트리의 활용

위에서 다뤘듯이 배열 자료구조는 검색에 특화되어있지만 삽입, 삭제 연산은 비효율적이다.

따라서 이진 검색 트리가 검색, 삽입, 삭제의 연산을 수행하는데 더 효율적인 자료구조라고 생각할 수 있다. 도서관에서 책을 검색하거나 학교에서 학생에 대한 정보를 저장하는 등 대량의 정보를 저장하고 검색할 때 이진 검색 트리가 활용되고 있다.

🧩 검색 트리의 종류

트리 명	트리 종류	검색 위치
이진 검색 트리 (기본)	이진 트리	메모리 (RAM)
AVL 트리	이진 트리 && 균형 검색 트리	메모리 (RAM)
레드-블랙 트리	이진 트리 && 균형 검색 트리	메모리 (RAM)
2-3-4 트리	다진 트리 && 균형 검색 트리	메모리 (RAM)
B-트리	다진 트리 && 균형 검색 트리	외장 메모리 (하드 디스크)

현재 가장 유명한 검색트리는 위의 5가지다. 오늘은 이 중 이진 검색트리와 AVL 트리를 다룬다. 먼저 위의 표에 대한 설명이다.

📌 이진 트리 && 다진 트리

한 노드가 칠 수 있는 가지의 수가 최대 2개인 트리를 이진 트리라고 한다.
반면에 다진 트리는 가지를 3개 이상 칠 수 있는 트리를 뜻한다.
용어가 헷갈릴 수 있는데 위의 이진 검색 트리가 가장 기본적인 이진 검색 트리이고 AVL 트리, 레드-블랙 트리가 더 발전된 이진 검색 트리라고 생각하면 된다.

📌 균형 검색 트리

이진 검색 트리는 검색할 때 이진 탐색 알고리즘을 사용한다. 그러나 만약 트리가 불균형하게 한쪽으로만 치우쳐져 있다면 검색 연산을 수행하는 평균 시간이 O(LogN) 에서 점점 O(N) 으로 늘어날 것이다. 불균형한 트리가 스스로 균형을 맞추도록 만들어진 트리를 균형 검색 트리라고 한다.

📌 검색 위치

대부분의 트리는 컴퓨터가 RAM에 불러온 뒤 연산을 실행한다. 하지만 트리의 용량이 RAM을 초과한다면 불가피하게 하드 디스크 같은 외장 메모리에 넣어두고 사용해야 한다. B-트리는 이러한 연산을 위해 만들어진 자료구조이다.

🧩 이진 검색 트리의 특징

이진 검색 트리는 다음과 같은 특징이 있다.

• 각 노드의 왼쪽 자식 노드의 키는 오른쪽 자식 노드의 키보다 작다.
• 왼쪽, 오른쪽 서브트리도 이진 검색 트리이다.
• 중복된 키를 허용하지 않는다.

이진 검색 트리의 모습

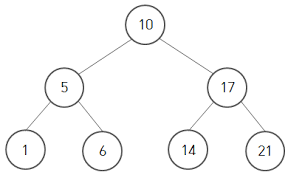
또 이진 검색트리는 왼쪽 자식 < 자신 < 오른쪽 자식 의 크기를 따르므로 중위 순회를 했을 때 정렬되어 출력되는 특징이있다.

🧩 이진 검색 트리 (기본)

검색 트리의 주요 연산은 검색, 삽입, 삭제다.

📌 검색 (Search)

먼저 검색의 경우 이진 탐색 알고리즘을 사용할 수 있으므로 평균 O(LogN) 의 시간이 걸린다. 하지만 기본적인 이진 검색 트리의 경우 아래와 같이 가지가 치우치면 최악의 경우 O(N) 의 시간이 소요된다.

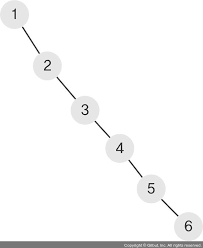
📌 삽입 (Insert)

삽입은 검색과 비슷하다. 검색 연산처럼 키의 자리를 찾은 뒤 노드를 추가해주기만 하면 된다. 따라서 평균 O(LogN), 최악의 경우 O(N) 의 시간이 소요된다.

📌 삭제 (Delete)

삭제는 검색이나 삽입보다 조금 더 복잡한 연산이 필요하다.
삭제 후에도 이진 검색 트리의 속성이 깨지면 안되기 때문에 그 자리를 대신할 노드를 찾고 바꿔주는데 시간이 소요된다. 삭제 연산은 당연히 검색, 삽입 연산보다 시간이 더 걸리지만 BigO 계산법으로 보면 똑같이 평균 O(LogN), 최악의 경우 O(N) 의 시간이 소요된다.

📌 정리

기본 이진 검색 트리에 대해 정리해보면 다음과 같다.

연산의 종류	평균 소요 시간	최악의 경우
검색 (기본)	O(LogN)	O(N)
삽입	O(LogN)	O(N)
삭제	O(LogN)	O(N)

📌 코드 구현 (Python)

node.py

각각의 노드는 item, left, right 의 멤버 변수를 갖는다.

class Node:
    def __init__(self, new_item, left, right):
        self.item = new_item
        self.left = left
        self.right = right

tree.py

from node import Node


class Tree:
    def __init__(self):
        self.__root = None
        self.__count = 0

    ## 같은 함수가 여러개인 이유
    ## 사용자는 매개변수로 찾고 싶은 값만 넣으면 된다.
    ## 하지만 재귀함수를 구현하려면 부모의 정보를 매개변수로 받아야 한다.

    # 검색
    def search(self, x) -> Node:
        return self.__search_item(self.__root, x)

    def __search_item(self, node: Node, x) -> Node:
        if node == None:
            return None
        elif x == node.item:
            return node
        elif x < node.item:
            return self.__search_item(node.left, x)
        else:
            return self.__search_item(node.right, x)

    # 삽입
    def insert(self, new_item):
        self.__root = self.__insert_item(self.__root, new_item)

    def __insert_item(self, node: Node, new_item) -> Node:
        if node == None:
            node = Node(new_item, None, None)
            self.__count += 1
        elif new_item < node.item:
            node.left = self.__insert_item(node.left, new_item)  # 왼쪽 가지
        elif new_item > node.item:
            node.right = self.__insert_item(node.right, new_item)  # 오른쪽 가지
        else:  # 중복되는 값 (x == node.item)
            print(f"{node.item}은(는) 중복되는 키이므로 insert 연산을 수행할 수 없습니다")
        return node

    # 삭제
    def delete(self, x):
        pre_cnt = self.__count
        self.__root = self.__delete_item(self.__root, x)
        if pre_cnt == self.__count:  # 이전 노드 개수랑 연산 후 노드 개수가 같으면
            print(f"{x}은(는) 존재하지 않는 키입니다!")

    def __delete_item(self, node: Node, x) -> Node:
        if node == None:  # item not found
            return None
        elif x == node.item:  # item found
            node = self.__delete_node(node)
            self.__count -= 1
        elif x < node.item:
            node.left = self.__delete_item(node.left, x)
        else:
            node.right = self.__delete_item(node.right, x)
        return node

    def __delete_node(self, node: Node) -> Node:
        if node.left == None and node.right == None:  # case 1(자식이 없음)
            return None
        elif node.left == None:  # case 2(오른쪽 자식만 있으면)
            return node.right
        elif node.right == None:  # case 2(왼쪽 자식만 있으면)
            return node.left
        else:  # case 3(두 자식 다 있으면)
            (item, r_node) = self.__delete_min_item(node.right)
            node.item = item
            node.right = r_node
            return node

    def __delete_min_item(self, node: Node) -> tuple:
        if node.left == None:  # 최솟값 노드를 찾음
            return (node.item, node.right)
        else:
            (item, r_node) = self.__delete_min_item(node.left)
            node.left = r_node
            return (item, node)

    # 빈 트리인지 확인
    def isEmpty(self) -> bool:
        return self.__root == None

    # 트리의 내용을 없앰
    def clear(self):
        self.__root = None

    # root를 반환
    def get_root(self):
        return self.__root

    # 노드의 개수를 반환
    def count(self):
        return self.__count

검색, 삽입, 삭제 연산 외에 isEmpty(), clear(), get_root(), count() 함수를 추가로 만들었다.

🧩 AVL 검색 트리

위에서 보았듯 일반적인 이진 검색 트리는 최악의 경우(트리의 균형이 치우쳐진 경우) 소요시간이 O(N) 에 가까워진다. AVL 검색 트리는 이같은 단점을 보완한 트리로 삽입과 삭제시 균형을 잡는 연산을 추가로 수행한다.

📌 검색 (Search)

검색 알고리즘은 위와 동일하게 이진 탐색을 사용한다. 그러나 AVL 트리는 항상 균형을 유지하고 있기 때문에 언제나 O(LogN) 의 시간이 소요된다.

📌 삽입 (Insert)

삽입, 삭제 연산은 위에서 했던 것과 같다. 하지만 AVL 트리는 항상 균형을 유지하고 있어야하기 때문에 삽입, 삭제 직후 균형을 잡는 연산을 추가로 수행한다. 기본 이진 검색 트리보다는 오래 걸리긴 하지만 그래도 O(LogN) 의 효율적인 속도를 보여준다.

📌 삭제 (Delete)

삽입 연산 시 깊이가 깊어져서 균형이 깨질 수 있다. 이때는 한번만 균형을 잡아주면 문제가 쉽게 해결된다. 하지만 삭제 연산은 깊이가 얕아져서 균형이 깨지는데, 균형을 잡아주는 과정에서 상위 트리까지 재귀적으로 균형이 깨질 수 있다. 그러나 삭제 연산 같은 경우에도 연산 시간은 O(LogN) 으로 효율적인 속도를 보여준다.

📌 정리

AVL 트리에 대해 정리해보면 다음과 같다.

연산의 종류	소요 시간
검색 (기본)	O(LogN)
삽입	O(LogN)
삭제	O(LogN)

📌 코드 구현 (Python)

node.py

균형을 체크할 때마다 높이를 계산하면 수행 시간이 너무 길어진다.
그러므로 높이를 담을 height 멤버 변수를 추가했다.

class Node:
    def __init__(self, new_item, left, right, height):
        self.item = new_item
        self.left = left
        self.right = right
        self.height = height

tree.py

from node import Node


class Tree:
    def __init__(self):
        self.__NIL = Node(None, None, None, 0)  # left = None, right = None 대신 참조할 노드
        self.__root = self.__NIL
        self.__count = 0  # 노드의 개수

        # 식별용 변수
        self.LL = 1
        self.LR = 2
        self.RR = 3
        self.RL = 4
        self.NO_NEED = 0
        self.ILLEGAL = -1

    # 검색
    def search(self, x):
        res = self.__search_item(self.__root, x)
        if res != self.__NIL:
            return res
        else:
            print(f"{x}은(는) 존재하지 않는 키입니다!")
            return None

    def __search_item(self, node: Node, x) -> Node:
        if node == self.__NIL:  # 없는 노드면
            return self.__NIL
        elif x == node.item:
            return node
        elif x < node.item:
            return self.__search_item(node.left, x)
        else:
            return self.__search_item(node.right, x)

    def insert(self, x):
        self.__root = self.__insert_item(self.__root, x)

    def __insert_item(self, node: Node, x) -> Node:
        if node == self.__NIL:
            node = Node(x, self.__NIL, self.__NIL, 1)
            self.__count += 1
        elif x < node.item:  # 왼쪽 가지로
            node.left = self.__insert_item(node.left, x)
            node.height = 1 + max(node.right.height, node.left.height)
            type = self.__check_balance(node)  # 수선할 AVL 타입 체크 (LL,LR,RR,RL)
            if type != self.NO_NEED:
                node = self.__balance_avl(node, type)
        elif x > node.item:  # 오른쪽 가지로
            node.right = self.__insert_item(node.right, x)
            node.height = 1 + max(node.right.height, node.left.height)
            type = self.__check_balance(node)  # 수선할 AVL 타입 체크 (LL,LR,RR,RL)
            if type != self.NO_NEED:
                node = self.__balance_avl(node, type)
        else:  # 중복되는 값 (x == node.item)
            print(f"{node.item}은(는) 중복되는 키이므로 insert 연산을 수행할 수 없습니다")
        return node

    def delete(self, x):
        pre_cnt = self.__count
        self.__root = self.__delete_item(self.__root, x)
        if pre_cnt == self.__count:  # 이전 노드 개수랑 연산 후 노드 개수가 같으면
            print(f"{x}은(는) 존재하지 않는 키입니다!")

    def __delete_item(self, node: Node, x) -> Node:
        if node == self.__NIL:
            return self.__NIL  # Item not found!
        if x == node.item:
            node = self.__delete_node(node)
            self.__count -= 1
        elif x < node.item:  # 왼쪽 가지로
            node.left = self.__delete_item(node.left, x)
            node.height = 1 + max(node.right.height, node.left.height)
            type = self.__check_balance(node)  # 수선할 AVL 타입 체크 (LL,LR,RR,RL)
            if type != self.NO_NEED:
                node = self.__balance_avl(node, type)
        else:  # 오른쪽 가지로
            node.right = self.__delete_item(node.right, x)
            node.height = 1 + max(node.right.height, node.left.height)
            type = self.__check_balance(node)  # 수선할 AVL 타입 체크 (LL,LR,RR,RL)
            if type != self.NO_NEED:
                node = self.__balance_avl(node, type)
        return node

    def __delete_node(self, node: Node) -> Node:
        if node.left == self.__NIL and node.right == self.__NIL:  # case 1(자식이 없음)
            return self.__NIL
        elif node.left == self.__NIL:  # case 2(오른자식뿐)
            return node.right
        elif node.right == self.__NIL:  # case 2(왼자식뿐)
            return node.left
        else:  # case 3(두 자식이 다 있음)
            (item, R_node) = self.__delete_min_item(node.right)
            node.item = item
            node.right = R_node
            node.height = self.__height(node)
            type = self.__check_balance(node)
            if type != self.NO_NEED:
                node = self.__balance_avl(node, type)
            return node

    def __delete_min_item(self, node: Node) -> tuple:
        if node.left == self.__NIL:  # 찾음
            return (node.item, node.right)

        (item, L_node) = self.__delete_min_item(node.left)
        node.left = L_node
        node.height = self.__height(node)
        type = self.__check_balance(node)
        if type != self.NO_NEED:
            node = self.__balance_avl(node, type)
        return (node, item)

    # 균형 잡기
    def __balance_avl(self, node: Node, type: int) -> Node:
        return_node = self.__NIL
        if type == self.LL:
            return_node = self.__right_rotate(node)  ## LL이면 우회전 한번
        elif type == self.LR:
            node.left = self.__left_rotate(node.left)
            return_node = self.__right_rotate(node)  ## LR이면 좌회전 한번, 우회전 한번
        elif type == self.RR:
            return_node = self.__left_rotate(node)  ## RR이면 좌회전 한번
        elif type == self.RL:
            node.right = self.__right_rotate(node.right)
            return_node = self.__left_rotate(node)  ## RL이면 우회전 한번, 좌회전 한번
        else:
            print("Imposible type! Should be one of LL,LR,RR,RL")

        return return_node

    # 좌회전
    def __left_rotate(self, node: Node) -> Node:
        R_child: Node = node.right
        if R_child == self.__NIL:
            raise Exception(node.item + "'s RChild shouldn't be NIL!")  # 논리 오류
        RL_child = R_child.left
        R_child.left = node
        node.right = RL_child
        node.height = 1 + max(node.left.height, node.right.height)
        R_child.height = 1 + max(R_child.left.height, R_child.right.height)
        return R_child

    # 우회전
    def __right_rotate(self, node: Node) -> Node:
        L_child: Node = node.left
        if L_child == self.__NIL:
            raise Exception(node.item + "'s RChild shouldn't be NIL!")  # 논리 오류
        LR_child = L_child.right
        L_child.right = node
        node.left = LR_child
        node.height = 1 + max(node.left.height, node.right.height)
        L_child.height = 1 + max(L_child.left.height, L_child.right.height)
        return L_child

    # 필요한 수선을 체크 후 반환 (LL,LR,RR,RL)
    def __check_balance(self, node: Node) -> int:
        type = self.ILLEGAL

        if node.left.height >= node.right.height + 2:  # L 유형
            if node.left.left.height >= node.left.right.height:
                type = self.LL
            else:
                type = self.LR
        elif node.right.height >= node.left.height + 2:  # R 유형
            if node.right.right.height >= node.right.left.height:
                type = self.RR
            else:
                type = self.RL
        else:
            type = self.NO_NEED
        return type

    # 노드의 높이
    def __height(self, node: Node) -> int:
        return 1 + max(node.left.height, node.right.height)

    def is_empty(self) -> bool:
        return self.__root == self.__NIL

    def clear(self):
        self.__root = self.__NIL

    def get_root(self):
        return self.__root

    # 전위순회
    def pre_order(self, node: Node):
        if node != self.__NIL:
            print(node.item)
            self.pre_order(node.left)
            self.pre_order(node.right)

    # 중위순회
    def in_order(self, node: Node):
        if node != self.__NIL:
            self.in_order(node.left)
            print(node.item)
            self.in_order(node.right)

    # 후위순회
    def post_order(self, node: Node):
        if node != self.__NIL:
            self.post_order(node.left)
            self.post_order(node.right)
            print(node.item)

    def count(self) -> int:
        return self.__count