문제
효주는 포도주 시식회에 갔다. 그 곳에 갔더니, 테이블 위에 다양한 포도주가 들어있는 포도주 잔이 일렬로 놓여 있었다. 효주는 포도주 시식을 하려고 하는데, 여기에는 다음과 같은 두 가지 규칙이 있다.
포도주 잔을 선택하면 그 잔에 들어있는 포도주는 모두 마셔야 하고, 마신 후에는 원래 위치에 다시 놓아야 한다.
연속으로 놓여 있는 3잔을 모두 마실 수는 없다.
효주는 될 수 있는 대로 많은 양의 포도주를 맛보기 위해서 어떤 포도주 잔을 선택해야 할지 고민하고 있다. 1부터 n까지의 번호가 붙어 있는 n개의 포도주 잔이 순서대로 테이블 위에 놓여 있고, 각 포도주 잔에 들어있는 포도주의 양이 주어졌을 때, 효주를 도와 가장 많은 양의 포도주를 마실 수 있도록 하는 프로그램을 작성하시오.
예를 들어 6개의 포도주 잔이 있고, 각각의 잔에 순서대로 6, 10, 13, 9, 8, 1 만큼의 포도주가 들어 있을 때, 첫 번째, 두 번째, 네 번째, 다섯 번째 포도주 잔을 선택하면 총 포도주 양이 33으로 최대로 마실 수 있다.
입력
첫째 줄에 포도주 잔의 개수 n이 주어진다. (1 ≤ n ≤ 10,000) 둘째 줄부터 n+1번째 줄까지 포도주 잔에 들어있는 포도주의 양이 순서대로 주어진다. 포도주의 양은 1,000 이하의 음이 아닌 정수이다.
출력
첫째 줄에 최대로 마실 수 있는 포도주의 양을 출력한다.
예제 입력
6
6
10
13
9
8
1
예제 출력
33
풀이
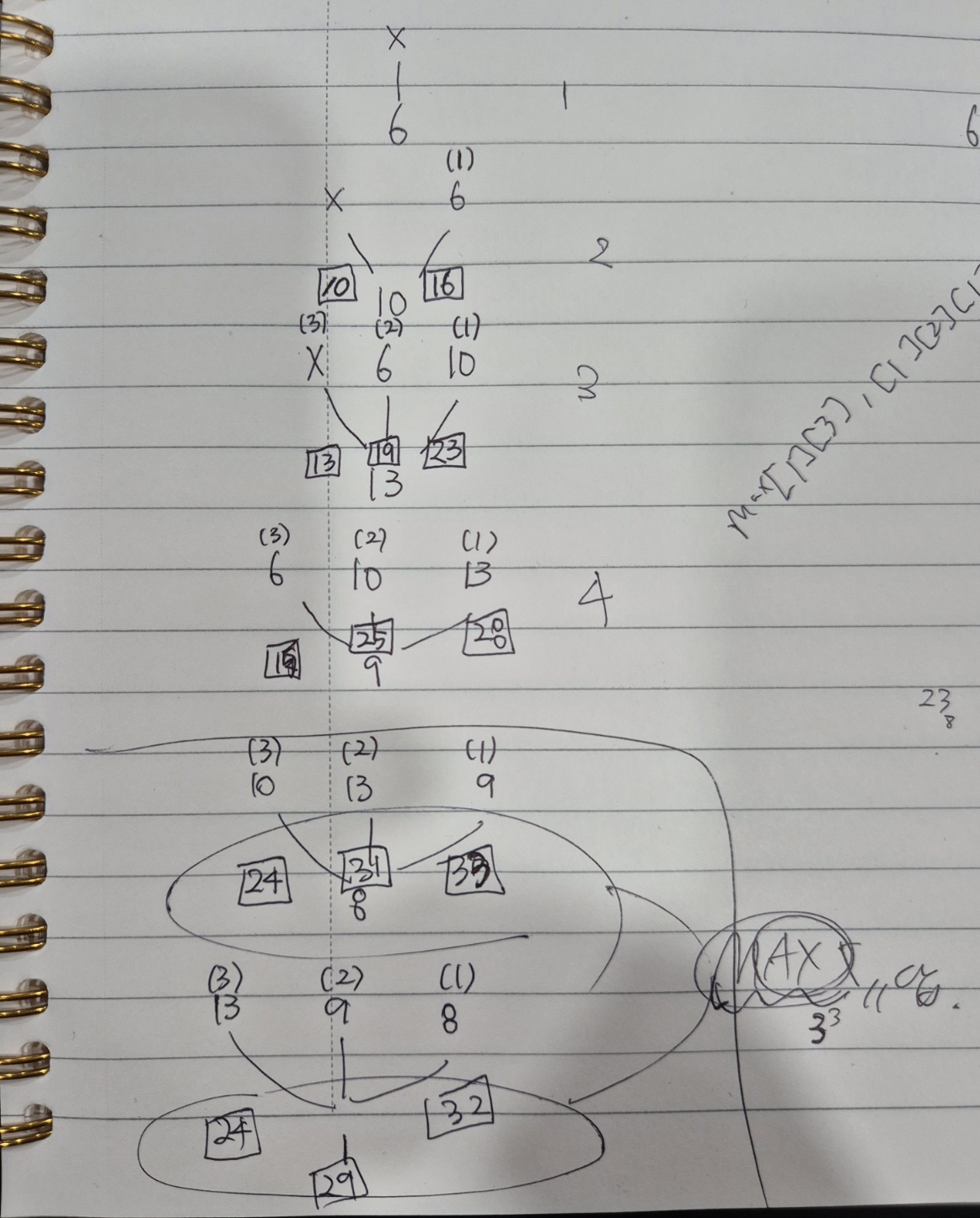풀이는 위와 같다. n번째 포도주를 마실때까지 최대로 마실 수 있는 포도주의 양을 점화식으로 나타내면 다음과 같다
f(n) = n번째 포도주를 마셨을때까지의 포도주 양의 최대값
1) n-1번째 포도주를 마신 후 n번째 포도주를 마실때
f(n) = arr[n] + MAX(f(n-1)+f(n-4), f(n-1)+f(n-3))
2) n-2번째 포도주를 마신 후 n번째 포도주를 마실때
f(n) = f(n) + MAX(f(n-2)+f(n-5),f(n-2)+f(n-4),f(n-2)+f(n-3))
3) n-3번째 포도주를 마신 후 n번째 포도주를 마실때
f(n) = f(n) + MAX(f(n-3)+f(n-6),f(n-3)+f(n-5),f(n-3)+f(n-4))
이렇게 하면 보기 힘들기 때문에 다음과 같이 바꿔보자
f(m,n) = n번째 포도주를 마신 후 m번째 포도주를 마셨을때까지 포도주 양의 최대값 (m > 3, 그 전 부분은 직접 할당해줘야 한다.)
arr[] = 포도주가 일렬로 담긴 공간(1부터 시작)
1) n = 1 일때
f(m,n) = arr[m] + MAX(f(m-1,3),f(m-1,2))
2) n = 2 일때
f(m,n) = arr[m] + MAX(f(m-2,3),f(m-2,2),f(m-2,1))
3) n = 3 일때
f(m,n) = arr[m] + MAX(f(m-3,3),f(m-3,2),f(m-3,1))
주의 사항
마지막 잔을 마셨을 때 포도주의 양이 최대일 수도 있고, 직전 잔을 마셨을 때 포도주의 양이 최대일 수도 있다. 따라서 두 경우 중 최대값을 출력해야 한다.
n = int(input())
arr = [0] * (n+1)
for i in range(1,n+1): arr[i] = int(input())
dp = [[0,0,0,0] for _ in range(n+1) ]
if n >= 1:
dp[1][3],dp[1][2],dp[1][1] = arr[1], arr[1],arr[1]
if n >= 2:
dp[2][3],dp[2][2],dp[2][1] = arr[2], arr[2],arr[1] + arr[2]
if n >= 3:
dp[3][3],dp[3][2],dp[3][1] = arr[3], arr[3]+arr[1], arr[3]+arr[2]
for i in range(4,n+1):
dp[i][3] = max(dp[i-3][3], dp[i-3][2], dp[i-3][1]) + arr[i]
dp[i][2] = max(dp[i-2][3], dp[i-2][2], dp[i-2][1]) + arr[i]
dp[i][1] = max(dp[i-1][3], dp[i-1][2]) + arr[i]
max1 = max(dp[n-1]) # n-1번줄까지의 최대값
max2 = max(dp[n]) # n번줄까지의 최대값
print(max(max1,max2))기타
나는 모든 경우에 대해 최적의 값을 모두 저장했는데(현단계에서 3,2,1칸 떨어진 포도주를 마셨을때의 각각의 포도주의 최대 양, 그 중 한가지 값이 최대값임), 다음과 같이 떨어진 칸 수에 상관없이 n번째 까지의 마실 수 있는 포도주의 양을 최대값 하나만 저장할 수도 있다. 이게 더 간단하고 이해하기도 쉬운 것 같다.
앞으로는 특정 단계까지 올 수 있는 (최적의 값을 포함한)모든 경우의 수를 구하기 보다는 해당 단계에서의 최적의 값만을 구해서 저장해보도록 해야겠다.
n = int(input())
wine = []
for i in range(n):
wine.append(int(input()))
d = [0]*n
d[0] = wine[0]
if n > 1:
# 두번째 포도주까지의 최대 양
d[1] = wine[0]+wine[1]
if n > 2:
# 세번째 포도주까지의 최대 양, 세번째 포도주를 안마실 수도 있음!
d[2] = max(wine[2]+wine[1], wine[2]+wine[0], d[1])
for i in range(3, n):
# i번째까지의 포도주의 최대 양, i번째 포도주를 안마실 수도 있음!
d[i] = max(d[i-1], d[i-3]+wine[i-1]+wine[i], d[i-2]+wine[i])
print(d[n-1])출처: https://hongcoding.tistory.com/48
풀이
위 방법을 참고하여 다시 풀어보았다. 세상 간단하네..
n = int(input())
arr = [0] * (n+1)
dp = [0]* (n+1)
for i in range(1,n+1): arr[i] = int(input())
if n >= 1: dp[1] = arr[1]
if n >= 2: dp[2] = arr[1]+arr[2]
if n >= 3: dp[3] = max(dp[3-1], arr[3]+arr[2]+dp[3-3], arr[3]+dp[3-2])
for i in range(4, n+1):
dp[i] = max(dp[i-1], arr[i]+arr[i-1]+dp[i-3], arr[i]+dp[i-2])
print(dp[n])