문제
한수는 크기가 2N × 2N인 2차원 배열을 Z모양으로 탐색하려고 한다. 예를 들어, 2×2배열을 왼쪽 위칸, 오른쪽 위칸, 왼쪽 아래칸, 오른쪽 아래칸 순서대로 방문하면 Z모양이다.
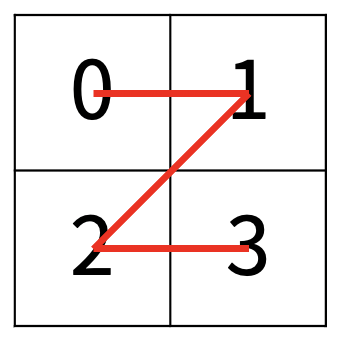
N > 1인 경우, 배열을 크기가 2N-1 × 2N-1로 4등분 한 후에 재귀적으로 순서대로 방문한다.
다음 예는 22 × 22 크기의 배열을 방문한 순서이다.
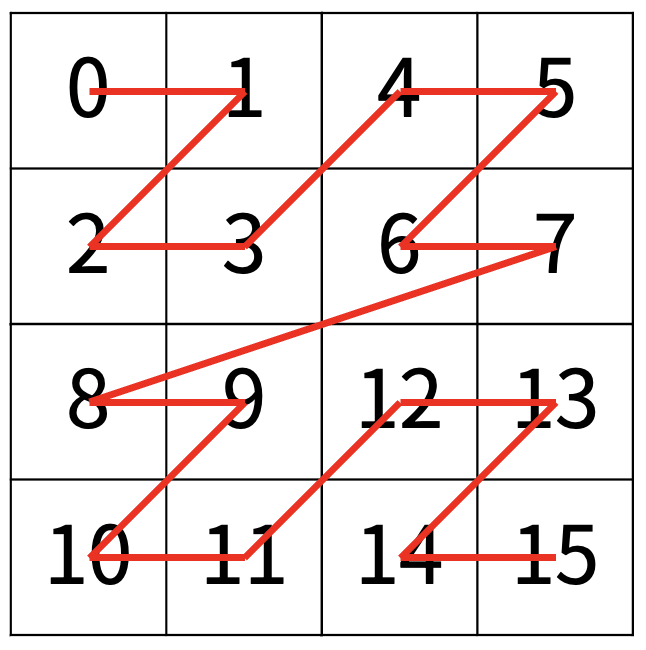
N이 주어졌을 때, r행 c열을 몇 번째로 방문하는지 출력하는 프로그램을 작성하시오.
다음은 N=3일 때의 예이다.
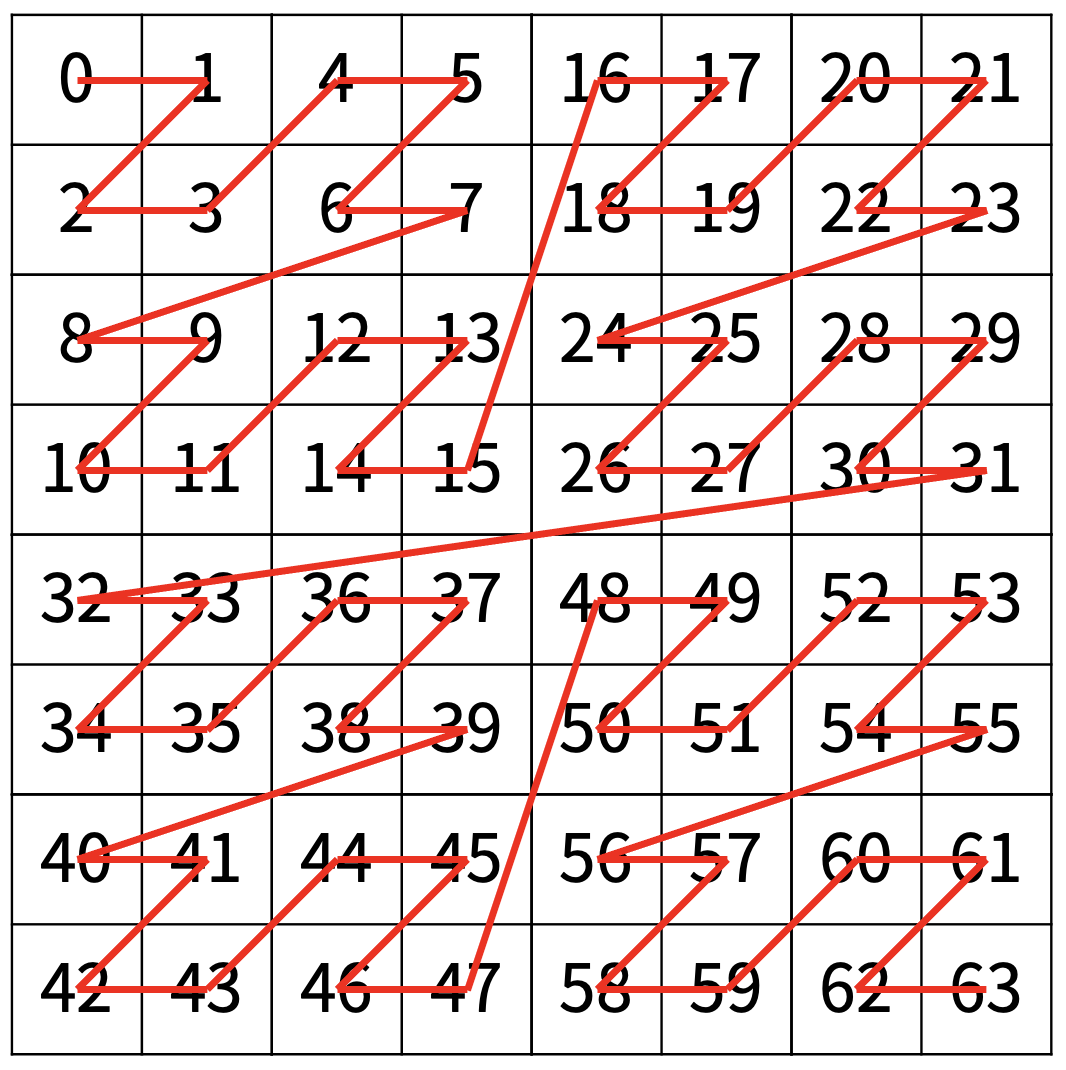
입력
첫째 줄에 정수 N, r, c가 주어진다.
출력
r행 c열을 몇 번째로 방문했는지 출력한다.
제한
1 ≤ N ≤ 15
0 ≤ r, c < 2N
예제 입력
2 3 1
예제 출력
11
풀이
처음에는 단순히 재귀를 이용해 4개의 사분면으로 쪼개서 다시 재귀함수를 호출해주는 방식을 생각해서 풀었는데 시간초과가 발생했다.
일반 재귀 풀이
n,r,c = map(int, input().split())
cnt = 0
arr = [[0 for _ in range(2**n)] for _ in range(2**n)]
def square(r,c,s):
global cnt
if s == 2:
arr[r][c] = cnt
cnt+=1
arr[r][c+1] = cnt
cnt+=1
arr[r+1][c] = cnt
cnt+=1
arr[r+1][c+1] = cnt
cnt+=1
return
else:
square(r,c,s//2)
square(r,c+s//2,s//2)
square(r+s//2,c,s//2)
square(r+s//2,c+s//2,s//2)
square(0,0,2**n)
print(arr[r][c])그래서 시간초과를 줄이는 방법을 고민했고, 모든 좌표들을 일일이 재귀로 거칠 필요 없이, 4개 사분면간의 규칙을 고려해 입력 받는 좌표에 관해서만 재귀 함수를 수행하도록 하였다.
예를 들어 3,7,7의 경우 8x8 배열, 시작지점이 (7,7)이고 4사분면이다.
(7,7)을 1사분면으로 이동시키면 (3,3)이 되고 이 경우 이동거리는 ((8//2)*2) 사분면의 차이(3)이므로 48이 된다.
그리고 다시 사각형의 크기를 1/4로 줄여서 재귀함수를 (2,3,3)로 호출해주면 (3,3)이 (1,1)로 이동하고, 이동거리는 기존의 48 + ((4//2)2) 사분면의 차이(3) 이므로 60이다.
그리고 다시 재귀함수를 (1,1,1)로 호출해준다. (1,1,1)의 경우 재귀함수의 탈출구, 종료지점이다. 이때는 현재 사분면-1 을 더한 후 종료해주면 된다.
시간단축 재귀 풀이
n,r,c = map(int, input().split())
cnt = 0
def rec(r,c,s):
global cnt
if s == 2:
if r == 0 and c == 0:cnt+=0
elif r == 0 and c == 1: cnt+=1
elif r ==1 and c == 0:cnt+=2
else: cnt+=3
return
if r< s//2 and c < s//2:
r,c = r,c # 그대로
elif r < s//2 and c >= s//2:
c = c-s//2
cnt+=((s//2)**2)
elif r >= s//2 and c < s//2:
r = r-s//2
cnt+=((s//2)**2)*2
else:
r,c = r-s//2, c-s//2
cnt+=((s//2)**2)*3
s = s//2
rec(r,c,s)
rec(r,c,(2**n))
print(cnt)정리
매 재귀함수 호출시, 좌표를 1사분면으로 이동시키고 누적합에 이동거리를 더해주면 된다. 현재 좌표의 사분면의 위치를 파악하고 바로 1사분면으로 이동시키면 되기 때문에 시간복잡도가 훨씬 줄어든다. 일반적인 재귀로는 8x8의 배열인 경우 약 21번이 필요하지만, 위의 방법을 사용하면 매번 크기가 1/4로 줄어들어 약 3번만에 연산이 가능하다.

