문제 - 신나는 함수 실행 (Silver2)
[백준 9184] https://www.acmicpc.net/problem/9184
풀이 전략
- 문제에 주어진 Pseudo Code는 재귀로 구현하는 코드이다. 하지만, 문제에서도 주어져 있듯이 재귀로 구현하면 상당히 오랜시간이 걸리기 때문에 다이나믹 프로그래밍으로 구현을 해야 한다.
참고
- 다이나믹 프로그래밍 (동적계획법)
우리말로는 동적 계획법이고, 동적 계획법의 경우 주어진 문제를 나눌 때 부분 문제를 최대한 많이 이용하도록 나눈 다음, 주어진 부분 문제의 정답을 한 번만 계산하고 저장해둔 뒤 다시 한 번 이 부분 문제를 이용할 때에는 저장해둔 정답을 바로 산출하여 이용함으로써 속도를 향상시킨다. 즉 그때그때 계산을 수행하는 재귀와 달리 동적계획법은 계산했던 값을 배열에 저장해 두었다가 나중에 꺼내서 사용하기 때문에 훨씬 계산이 빨라지게 된다.
즉, 동적 계획법은 그림과 같이 최적 부분 구조(Optimal Substructure)를 지닌 중복된 하위 문제들(Overlapping Subproblems)을 분할 정복으로 풀이하는 문제해결 패러다임이다.
대표적으로는 피보나치 수열을 푸는 문제가 있다.
피보나치 함수의 경우는 배울 때는 재귀로 배웠다. 그 이유가 n에 큰 수를 넣지 않기 때문이고, 재귀를 배울고 이해하기에는 피보나치함수 만한게 없기 때문이다. 하지만 n에 큰 수가 들어가게 되면 재귀의 특성상 엄청난 계산양을 필요로 하기 때문에 시간초과가 날 가능성이 상당히 높아진다. 따라서 피보나치함수도 동적계획법을 활용하여 구현을 하면 시간이 훨씬 빨라지게 된다.int fib(int n){ if(n==1 or n==2){ return 1; }else{ return fib(n-1)+fib(n-2); } } // 재귀 int fibonacci(int n){ int f[n]; f[1]=f[2]=1; for(int i=3;i<=n;i++){ f[i]=f[i-1]+f[i-2]; } return f[n]; } // 다이나믹 프로그래밍위에껀 재귀, 아래껀 동적계획법으로 구현한 코드이다.
얼핏보면 아래 코드도 재귀를 이용한 것 처럼 보이지만, 다른 점은 f라는 배열에서 현재 위치에 이전 두개의 값을 더한 값을 저장해 놓는다는 점이다. 그렇기 때문에 n이 입력값으로 주어지게 되면 배열에 n번째 index에 해당하는 값을 찾기만 하면 답을 구할 수 있게 된다.
하지만, 재귀는 입력값이 주어지게 되면 그때그때 연산을 수행하기 때문에 입력값이 여러개가 주어지게 된다면 연산 수행시간이 배로 늘어날 수 밖에 없다.
소스 코드
#include <iostream>
#include <vector>
using namespace std;
// int w(int a, int b, int c){
// if(a<=0 || b<=0 || c<=0){
// return 1;
// }else if(a>20 || b>20 || c>20){
// return w(20,20,20);
// }else if(a<b && b<c){
// return w(a,b,c-1)+w(a,b-1,c-1)-w(a,b-1,c);
// }else{
// return w(a-1,b,c)+w(a-1,b-1,c)+w(a-1,b,c-1)-w(a-1,b-1,c-1);
// }
// }
// 문제에 주어진 Pseudo Code
const int MAX_NUM=21;
vector<vector<vector<int>>> memo(MAX_NUM,vector<vector<int>>(MAX_NUM,vector<int>(MAX_NUM,-1)));
// 삼중벡터로 3개의 입력값을 vector에 저장
int w(int a, int b, int c){
if(a<=0 || b<=0 || c<=0){
return 1;
}else if (a>20 || b>20 || c>20){
return w(20,20,20);
}
// 여기까지는 재귀와 동일
if(memo[a][b][c]!=-1){
return memo[a][b][c];
} // a==-1 || b==-1 || c==-1 이 아닐 때
if(a<b && b<c){
memo[a][b][c]=w(a,b,c-1)+w(a,b-1,c-1)-w(a,b-1,c);
}else{
memo[a][b][c]=w(a-1,b,c)+w(a-1,b-1,c)+w(a-1,b,c-1)-w(a-1,b-1,c-1);
}
return memo[a][b][c];
}
int main(void){
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int a,b,c;
while(1){
cin>>a>>b>>c;
if(a==-1 && b==-1 && c==-1){
break;
} (a,b,c)=(-1,-1,-1)이면 입력을 멈춤
int answer=w(a,b,c);
cout<<"w("<<a<<", "<<b<<", "<<c<<") = "<<answer<<'\n';
}
return 0;
}[결과]
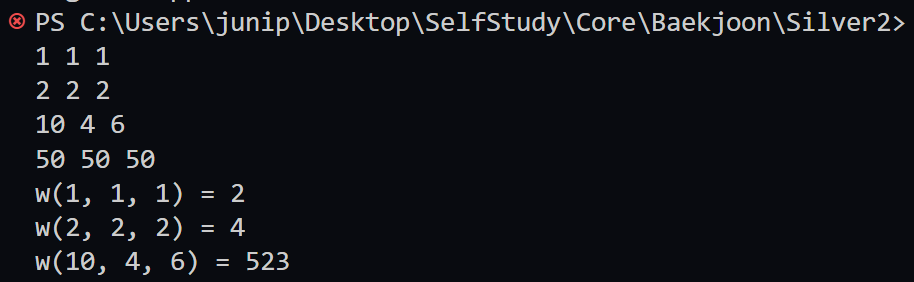
<재귀>
위의 그림을 보면 알겠지만, a,b,c가 15보다 큰 수를 입력을 받게 되면 컴파일러가 계산을 하는데 너무 오랜 시간이 걸려서 50 50 50에서 더이상 입력값을 받지 못하게 된다.
따라서 재귀로 구현을 하면 이 문제는 풀 수가 없다.
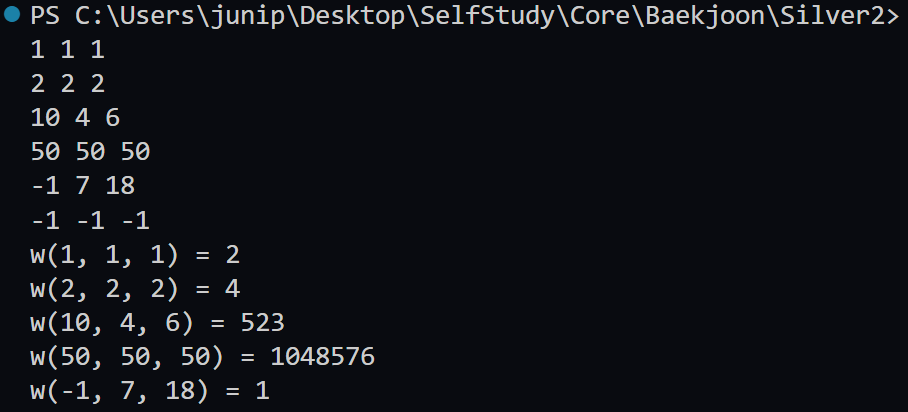
<동적계획법>