[C++] 백준 7561 - 크래머의 공식

문제 - 크래머의 공식 (Gold 4)

[백준 7561] https://www.acmicpc.net/problem/7561

풀이 전략

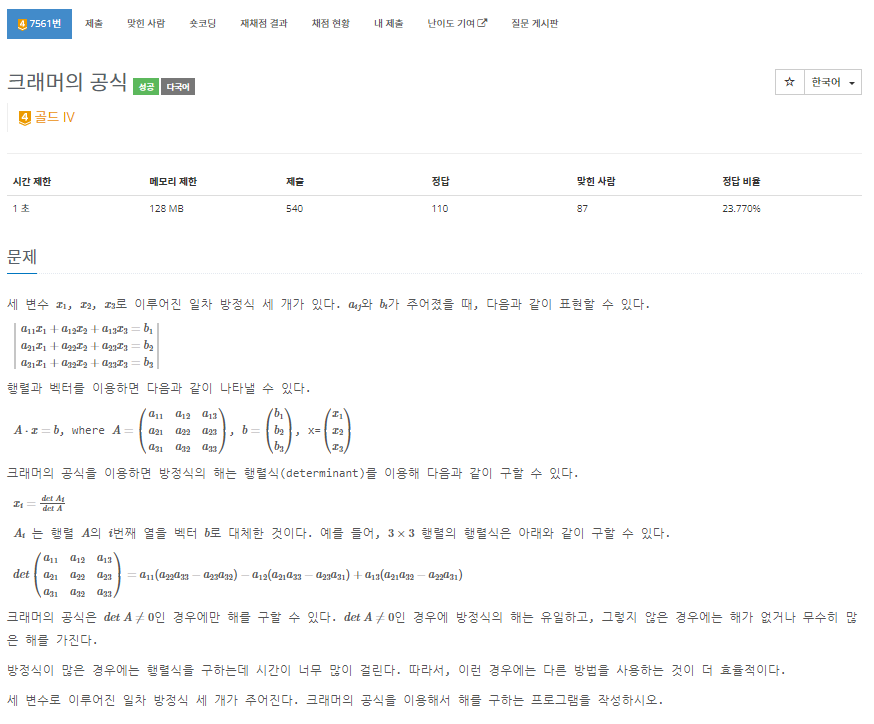
• 크래머 공식을 알고 있으면 그냥 구현만 하면 된다. 하지만, 문제 조건 중에서

• 방정식이 많은 경우에는 행렬식을 구하는데 시간이 너무 많이 걸린다. 따라서, 이런 경우에는 다른 방법을 사용하는 것이 더 효율적이다.
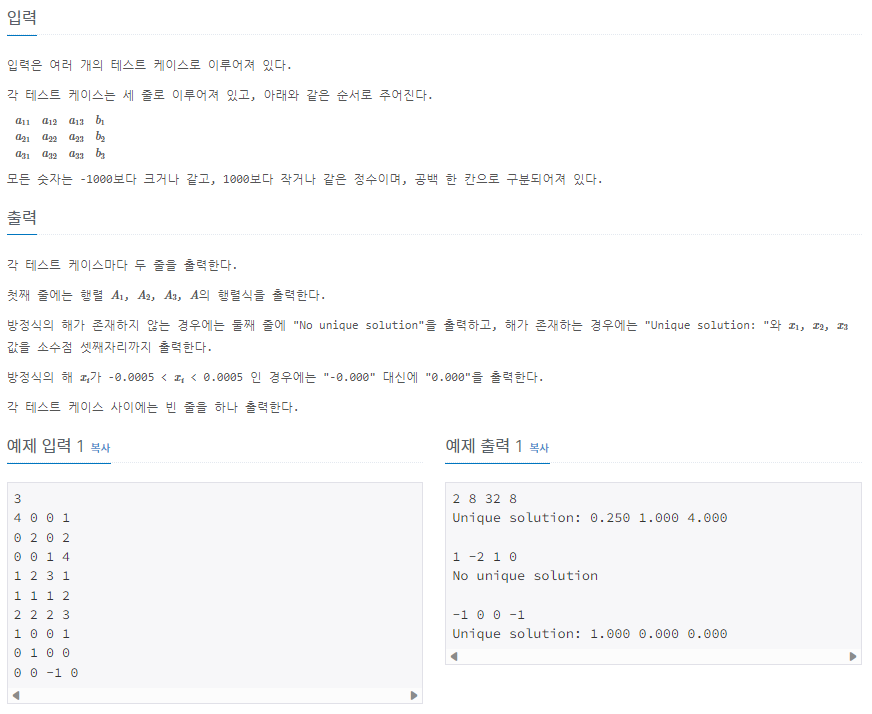
• 값을 소수점 셋째자리까지 출력한다.
• 방정식의 해 x가 -0.0005 < x < 0.0005 인 경우에는 "-0.000" 대신에 "0.000"을 출력한다.

이러한 조건들을 맞춰주는게 까다로울 것 같고, 특히 자료형에 신경을 많이 써야 한다.

참고

크래머의 공식

: 여러개의 연립 방정식의 해를 구하는데 효율적인 방법으로, 특정 미지수의 값을 바로 구할 수 있다.

크래머 공식에 대한 설명은 문제에서도 나와있지만, 적어보자면

$\\ \begin{cases} a_1x+b_1y+c_1z=d_1\\ a_2x+b_2y+c_2z=d_2\\ a_3x+b_3y+c_3z=d_3 \end{cases}$

$denominator=\begin{vmatrix}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3 \end{vmatrix}$

$numerator_x=\begin{vmatrix}d_1&b_1&c_1\\d_2&b_2&c_2\\d_3&b_3&c_3 \end{vmatrix}$
$numerator_y=\begin{vmatrix}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3 \end{vmatrix}$
$numerator_z=\begin{vmatrix}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3 \end{vmatrix}$

$x=$$numerator_x/denominator$
$y=$$numerator_y/denominator$
$z=$$numerator_z/denominator$

이런 식으로 미지수의 해를 바로 구할 수 있다.

소스 코드

#include <iostream>
#include <cmath>
#include <vector>
using namespace std;

int main(void){
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);

    int N;
    cin>>N;

    vector<vector<int>> A(3,vector<int>(4,0)); // 3행 4열짜리 행렬
    vector<long long> B; // 자료형 주의!

    double detA1,detA2,detA3,detA,detA1B,detA2B,detA3B;
    for(int t=0;t<N;t++){
        for(int i=0;i<3;i++){
            for(int j=0;j<4;j++){
                cin>>A[i][j];
            }
        }
        detA1B=A[0][3]*(A[1][1]*A[2][2]-A[1][2]*A[2][1])
        	-A[0][1]*(A[1][3]*A[2][2]-A[1][2]*A[2][3])
            +A[0][2]*(A[1][3]*A[2][1]-A[1][1]*A[2][3]);
            // numerator_x
        detA2B=A[0][0]*(A[1][3]*A[2][2]-A[1][2]*A[2][3])
        	-A[0][3]*(A[1][0]*A[2][2]-A[1][2]*A[2][0])
            +A[0][2]*(A[1][0]*A[2][3]-A[1][3]*A[2][0]);
            // numerator_y
        detA3B=A[0][0]*(A[1][1]*A[2][3]-A[1][3]*A[2][1])
        	-A[0][1]*(A[1][0]*A[2][3]-A[1][3]*A[2][0])
            +A[0][3]*(A[1][0]*A[2][1]-A[1][1]*A[2][0]);
            // numerator_z

        detA1=A[0][0]*(A[1][1]*A[2][2]-A[1][2]*A[2][1]);
        detA2=A[0][1]*(A[1][0]*A[2][2]-A[1][2]*A[2][0]);
        detA3=A[0][2]*(A[1][0]*A[2][1]-A[1][1]*A[2][0]);

        detA=detA1-detA2+detA3;
        //denominator
        
        // 식이 난잡하지만, 위에서 설명한 크래머 공식을 구현한거임

        B.push_back(detA1B);
        B.push_back(detA2B);
        B.push_back(detA3B);
        B.push_back(detA);
        // B에 출력해야 하는 값을 저장

        for(int i=0;i<B.size();i++){
            cout<<B[i]<<" ";
        }
        cout<<'\n';

        if(detA==0){
            cout<<"No unique solution\n";
        }else{
            cout<<fixed;
            cout.precision(3); // 소수점 3자리로 고정
            cout<<"Unique solution: "<<(abs(detA1B/detA)<0.0005?0.000:detA1B/detA)<<" "
                <<(abs(detA2B/detA)<0.0005?0.000:detA2B/detA)<<" "
                <<(abs(detA3B/detA)<0.0005?0.000:detA3B/detA)<<'\n';}
                // 절댓값이 0.0005보다 작으면 0.000 출력, 아니면 그대로 나눈 값 출력
        if(t!=N-1){
            cout<<'\n';
        } // 마지막 줄은 한 줄 띄어쓰기 생략
        B.clear();
        // 새로운 입력 값을 받기 위해 B를 초기화
    }
}

결과

결론

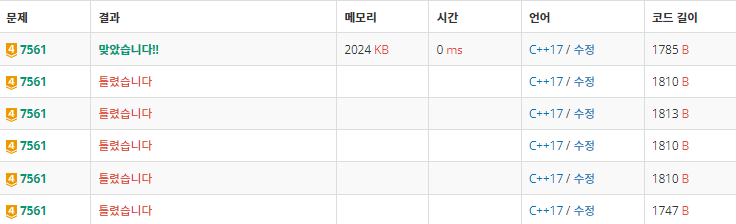
• 자료형 long long 때문에 결과가 제대로 출력됨에도 불구하고 25%에서 5번 넘게 틀렸었다.
  25%에서 멈춘다? 그러면 경험상 자료형이 틀렸을 확률이 높으니 고려해보자.
• 행렬식을 구하는 코드가 상당히 난잡해서 저걸 반복문이든 조건문이든 어떤 방식을 사용해서라도 간단하게 할 방법을 생각해봐야 할 것 같다. 내가 쓴 코드여서 난 금방 알아보지만, 다른 사람들이 보면 저 코드가 뭔가 싶을 것 같다.