Java에서 팩토리얼을 구현하는 방법 (다리놓기 - 조합)

문제

풀이 방법 설계

문제를 해석해보면,
만들어져야 하는 다리의 수는 왼쪽 사이트 개수인 N이고
N의 입장에서 서로 중복되지 않게 M을 선택하면 된다.

바꿔 말하면 그냥 오른쪽 사이트인 M개 중 N개를 고르면 된다. (mCn)
문제에서 교차는 불가하다고 했는데 어차피 M개 중 N개를 무작위로 고르면
왼쪽 사이트에서 위에서부터 차례로 이어주면 되기 때문에 교차를 따로 신경쓰지 않아도 된다.

mCn 구현1  -  mCn = m! / ((m-n)! * n!)

조합 공식의 기본인 팩토리얼을 그대로 이용한 구현

package baekjoon.silver.five.다리놓기;

import java.io.*;
import java.math.BigInteger;

public class Main {

    public static void main(String[] args) throws IOException{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        int num = Integer.parseInt(br.readLine());
        for(int i = 0; i< num; i++){
            String[] arr = br.readLine().split(" ");
            int n = Integer.parseInt(arr[1]);
            int r = Integer.parseInt(arr[0]);
            bw.write(factorial(BigInteger.valueOf(n)).divide(factorial(BigInteger.valueOf(n-r)).multiply(factorial(BigInteger.valueOf(r))))+ "\n");
        }
        bw.flush();
    }
    
    /**
      3
      2 2
      1 5
      13 29
     */
    public static BigInteger factorial(BigInteger n){
        if(n.equals(BigInteger.valueOf(1))  || n.equals(BigInteger.valueOf(0))) return BigInteger.valueOf(1);
        return n.multiply(factorial(n.subtract(BigInteger.valueOf(1)))) ;
    }
}

주목할 점은 int나 long은 사용불가하다는 것이다.

문제에서 제시된 M의 최대값은 30인데,
분자를 얻기 위해 30!을 그대로 돌려버리면 int의 32비트 공간은 물론 long의 64비트 저장공간까지 가뿐히 뛰어넘는다.
64비트 공간을 사용한다는건 이진수로 표현 가능한 자리가 64자리 즉 2의 63승까지 표현가능하다는 것인데,
얼추 계산해봐도 30부터 1까지 떨어지는 30번의 곱이 2의 63승보다 훨씬 크다.
그 결과 long이 가지는 최대 저장 공간을 넘어가버려 위와 같이 의미 없는 수가 나타나게 된다.
그래서 자바에서 제공하는 무한의 수를 담을 수 있는 타입인 BitInteger를 사용해야 한다.

BigIntger의 경우 불변 타입으로 연산자를 이용한 직접적인 연산이 불가하고 새로운 객체를 생성하기 위해 내부 메소드를 사용해야 하기 때문에 연산 시 손이 조금 더 간다는(?) 단점이 있다.
팩토리얼을 이용한 방법은 계산 과정에서 도출되는 수의 크기가 클 뿐이지
연산의 비용이 큰 것은 아니므로 실전에서도 활용 가능하다.

mCn 구현2  -  mCn = m-1Cn + m-1Cn-1

이항계수를 그림으로 나타낸 파스칼의 삼각형의 성질을 이용해서 푸는 방법이다.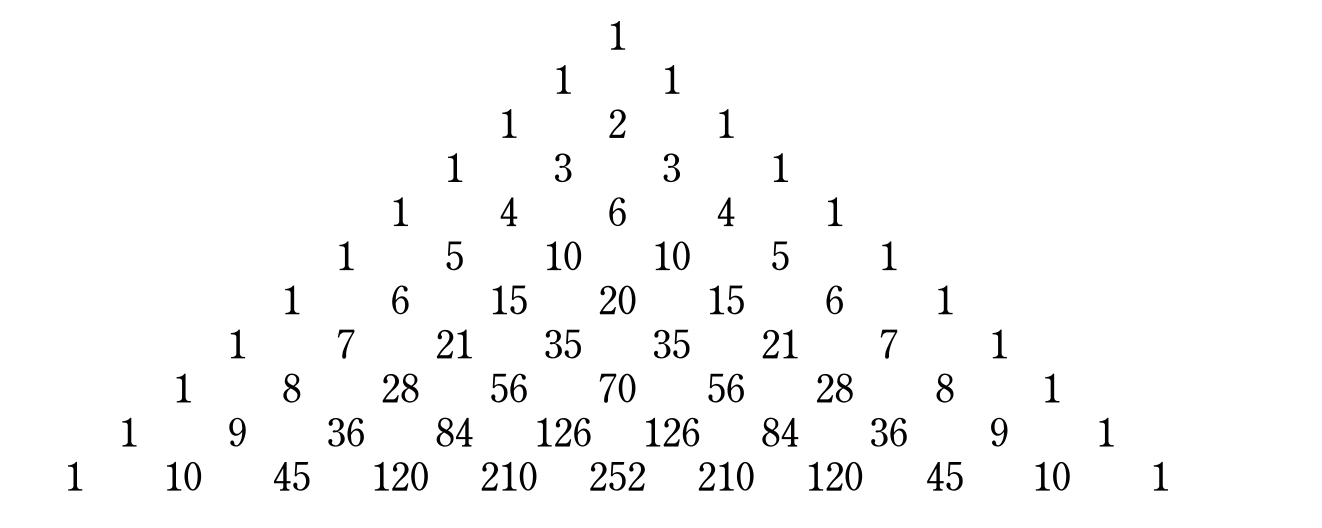파스칼의 삼각형은 기본적으로 윗 줄의 좌우측 숫자를 더해 가운데 아래로 내리는 형태를 가진다.
그런데 파스칼의 삼각형을 잘 보면 nCr을 통해 구현할 수 있다.
세 번째 줄부터 보면,   1,3,3,1 -> 3C0, 3C1, 3C2, 3C3
네 번째 줄을 보면,   1,4,6,4,1 -> 4C0, 4C1, 4C2, 4C3, 4C4,
...
n 번째 줄을 보면,   nC0, nC1, ... , nCn-1, nCn
와 같은 규칙을 통해 만들어진다.
즉 파스칼의 삼각형은 조합 공식을 이용해 만들어진다는 것이다.

이는 반대로 조합공식을 파스칼 삼각형의 성질을 이용해 구할 수 있다는 것을 말한다.

mCn = m-1Cn + m-1Cn-1 

이 식이 파스칼을 이용하여 mCn을 구한 것이다.

파스칼 삼각형을 이용한 구현

package baekjoon.silver.five.다리놓기;

import java.io.*;
import java.math.BigInteger;

public class Main {

    public static void main(String[] args) throws IOException{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        int num = Integer.parseInt(br.readLine());
        for(int i = 0; i< num; i++){
            String[] arr = br.readLine().split(" ");
            int n = Integer.parseInt(arr[1]);
            int r = Integer.parseInt(arr[0]);
            memory = new int[n+1][r+1];
            bw.write(solution(n,r)+ "\n");
        }
        bw.flush();
    }

    static int[][] memory;

    /**
3
2 2
1 5
13 29
     */
    public static int solution(int n, int r){
        if(memory[n][r] != 0) return memory[n][r];
        if(n == r || r == 0) return 1;
        int result = solution(n-1,r-1) + solution(n-1, r);
        memory[n][r] = result;
        return result;
    }

풀이 설명

주어진 mCn 에 대해 m-1Cn-1 + m-1Cn-1 을 재귀 호출하여 값을 구하되
이미 계산한 값에 대해서는 다시 계산하지 않고 이전 값을 이용할 수 있도록 하였다.