💡 힙 Heap 정리

📌 힙(Heap)이란?

힙(Heap)은 완전 이진 트리(Complete Binary Tree) 기반의 자료구조로, 최댓값 또는 최솟값을 빠르게 찾을 수 있도록 구성된 트리이다.
부모 노드가 자식 노드보다 크거나 작다는 특징을 가진다.

📌 힙(Heap)의 특징

1. 완전 이진 트리(Complete Binary Tree)
   마지막 레벨을 제외하면 모든 노드가 왼쪽부터 채워져 있어야 함.
   즉, 배열(Array)로 표현하기 쉬움.

2. Heap Property(힙 속성)
   최소 힙(Min-Heap) : 부모 노드 ≤ 자식 노드 → 최솟값이 루트(root)에 위치
   최대 힙(Max-Heap) : 부모 노드 ≥ 자식 노드 → 최댓값이 루트(root)에 위치

3. 빠른 삽입/삭제 연산
   삽입 (O(log N)) : 새로운 노드를 추가한 후 Heapify Up(힙 상향) 수행.
   삭제 (O(log N)) : 루트 노드를 제거한 후 Heapify Down(힙 하향) 수행.

📌 힙(Heap)의 종류

1. 최소 힙 (Min-Heap)

• 부모 노드가 항상 자식보다 작거나 같음.
• 루트(root)에는 최솟값이 위치.
• PriorityQueue(기본 설정)

       1
     /   \
    3     5
   / \   /
  7   9 6

poll()을 하면 1이 제거되고, 다음 최솟값(3)이 루트로 올라옴.

2. 최대 힙 (Max-Heap)

• 부모 노드가 항상 자식보다 크거나 같음.
• 루트(root)에는 최댓값이 위치.
• PriorityQueue<>(Collections.reverseOrder()) 사용

       9
     /   \
    7     6
   / \   /
  3   5 1

poll()을 하면 9가 제거되고, 다음 최댓값(7)이 루트로 올라옴.

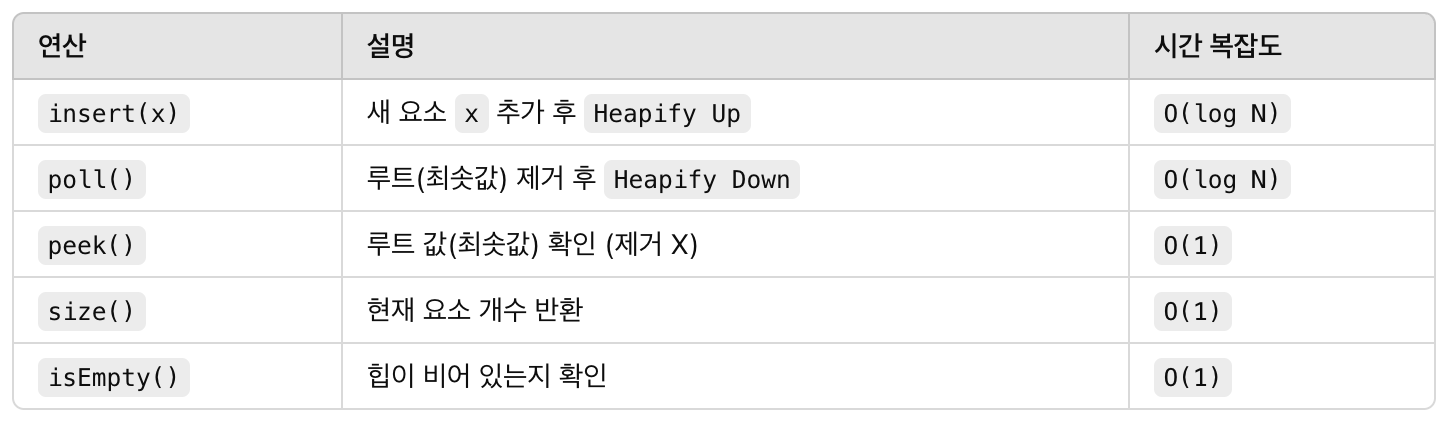
📌 힙(Heap)의 연산 (Min-Heap 기준)

📌 힙(Heap)의 구현 (Java)

1. Min-Heap (최소 힙)

import java.util.PriorityQueue;

public class MinHeapExample {
    public static void main(String[] args) {
        PriorityQueue<Integer> minHeap = new PriorityQueue<>();

        minHeap.add(5);
        minHeap.add(1);
        minHeap.add(8);
        minHeap.add(3);

        System.out.println(minHeap.poll()); // 1
        System.out.println(minHeap.poll()); // 3
        System.out.println(minHeap.poll()); // 5
        System.out.println(minHeap.poll()); // 8
    }
}

• 기본적으로 자바의 PriorityQueue는 Min-Heap으로 동작
• poll()을 하면 오름차순(작은 값부터)으로 요소가 제거됨

2. Max-Heap (최대 힙)

import java.util.PriorityQueue;
import java.util.Collections;

public class MaxHeapExample {
    public static void main(String[] args) {
        PriorityQueue<Integer> maxHeap = new PriorityQueue<>(Collections.reverseOrder());

        maxHeap.add(5);
        maxHeap.add(1);
        maxHeap.add(8);
        maxHeap.add(3);

        System.out.println(maxHeap.poll()); // 8
        System.out.println(maxHeap.poll()); // 5
        System.out.println(maxHeap.poll()); // 3
        System.out.println(maxHeap.poll()); // 1
    }
}

• Collections.reverseOrder()를 사용하면 Max-Heap으로 동작
• poll()을 하면 내림차순(큰 값부터)으로 요소가 제거됨

📌 힙(Heap)의 활용 예시

• 우선순위 큐(Priority Queue)
  작업 스케줄링 (예: CPU 프로세스 우선순위 처리)
  네트워크 패킷 처리 (먼저 온 패킷을 먼저 처리)
• 힙 정렬(Heap Sort)
  O(N log N)의 정렬 알고리즘 (퀵 정렬과 비슷한 성능)
• 다익스트라 알고리즘 (Dijkstra’s Algorithm)
  최단 경로 찾기에서 우선순위 큐를 사용하여 최단 거리 노드 선택
• K번째 최댓값/최솟값 찾기
  k개까지만 유지하면서 poll()을 이용해 K번째 최소/최대 값 찾기