에라토스테네스의 체

에라토스테넷스의 체 알고리즘

: 다수의 자연수에 대하여 소수 여부를 판별할 때 사용하는 대표적 알고리즘
: 특정 범위안에 존재하는 각각의 자연수들이 소수인지 아닌지를 한꺼번에 계산하고자 할 때 효과적으로 사용

동작과정

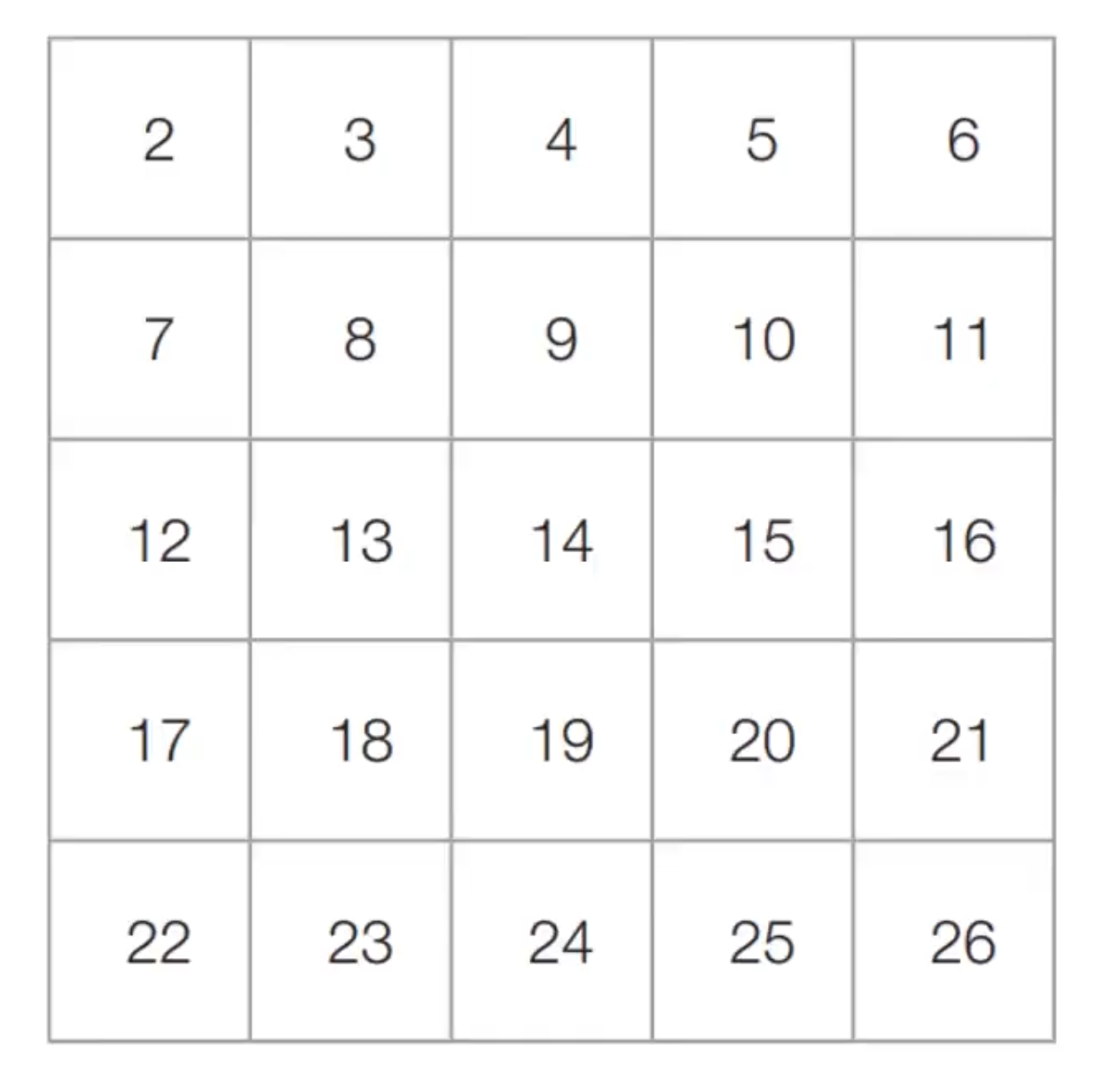
➀ 2부터 N까지의 모든 자연수를 나열한다.
➁ 남은 수 중에서 아직 처리하지 않은 가장 작은 수 i를 찾는다.
➂ 남은 수 중에서 i의 배수를 모두 제거한다(i는 제거하지 않음)
➃ 더 이상 반복할 수 없을 때까지 2번과 3번의 과정을 반복한다.

ex)

N = 26인 경우,

1. 2부터 26까지 모든 자연수 나열
   

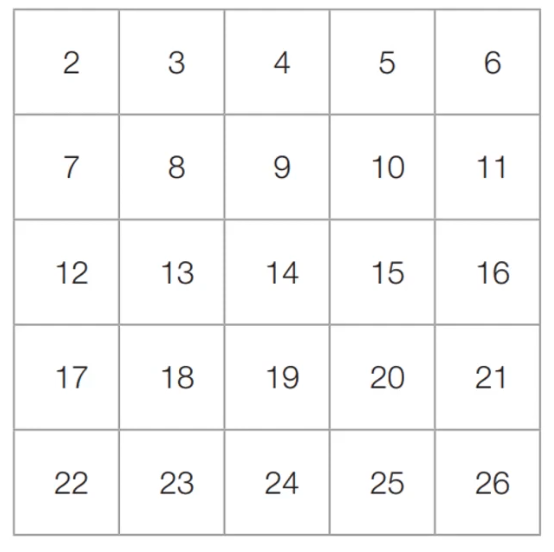
2. 아직 처리하지 않은 가장 작은 수 2를 제외한 2의 배수는 모두 제거
   

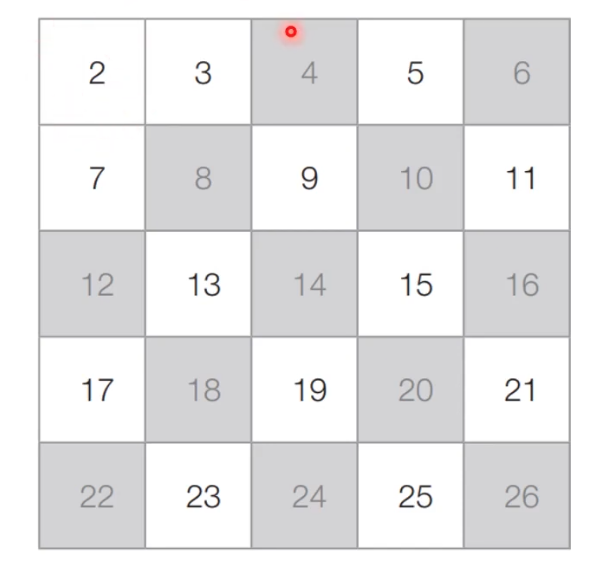
3. 아직 처리하지 않은 가장 작은 수 3를 제외한 3의 배수는 모두 제거
   

4. 아직 처리하지 않은 가장 작은 수 5를 제외한 5의 배수는 모두 제거
   

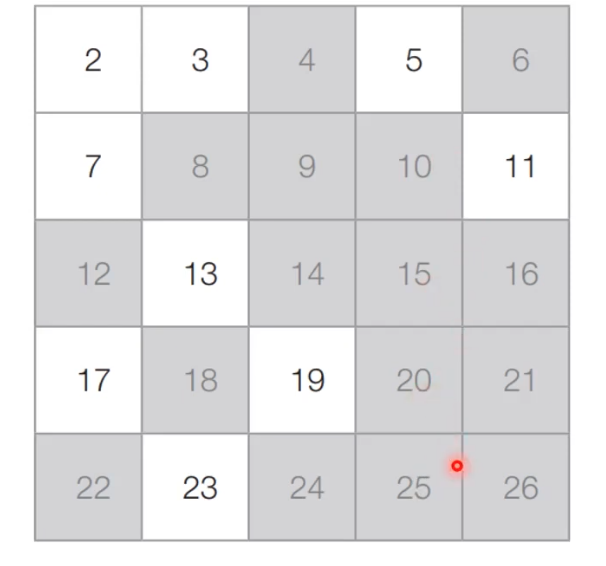
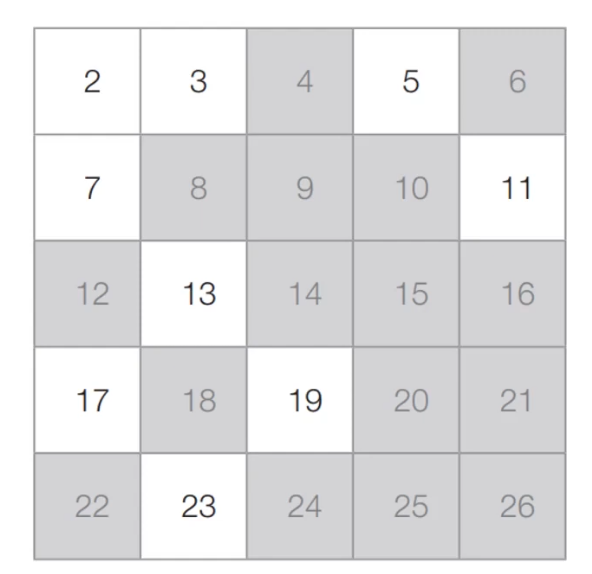
5. 앞의 과정을 반복했을때 최종 결과는
   

코드로 구현하면 😎

n = 1000
array = [True for i in range(n+1)]           [1]

for i in range(2, int(math.sqrt(n)) + 1):
	if array[i] == True:                     [2]
    	j = 2                                [3]
        while i * j <= n:
        	array[i*j] = False
            j += 1
            
for i in range(2, n+1):                      [4]
	if array[i]:
    	print(i, end = ' ')

[1] 모든 수가 소수(True) 인것으로 초기화(0,1은 제외)
[2] i가 소수인 경우
[3] i를 제외한 i의 모든 배수 지우기
[4] 모든 소수 출력

장점

• 알고리즘의 시간 복잡도는 선형 시간에 가까울 정도로 매우 빠르다.

단점

• 각 자연수에 대한 소수 여부를 저장해야 하므로 메모리가 많이 필요하다.