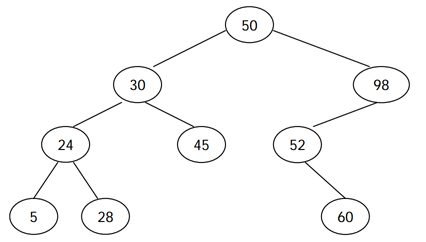
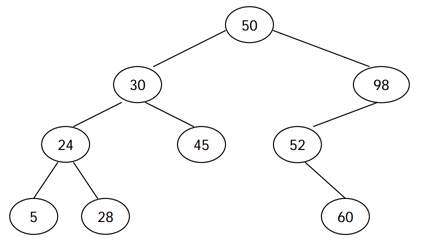
전위 -> 후위
- 트리의 노드 값을 x 축으로 내린다고 생각하면 :
5 - 24 - 28 - 30 -45 - 50 - 52 - 60 - 98(정렬!) 50을 기준으로 왼쪽/오른쪽 서브트리로 분리
import sys
sys.setrecursionlimit(10**9)
pre = []
while True:
try:
pre.append(int(sys.stdin.readline()))
except:
break
def postorder(start, end):
if start > end:
return
mid = end +1
for i in range(start+1, end+1):
if pre[start] < pre[i]:
mid = i
break
postorder(start+1, mid-1)
postorder(mid, end)
print(pre[start])

| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| Value | 50 | 30 | 24 | 5 | 28 | 45 | 98 | 52 | 60 |
1) 이진 탐색 시작 : postorder(0, len(preorder) -1) = 첫번째 노드 Index, 마지막 노드 Index 전달
2) 서브트리의 루트 찾기
for i in range(start+1, end+1): 루트의 값과 루트+1~마지막까지의 값들을 비교하기pre[start] < pre[i]: 이때 pre[i]의 값은 루트에서 오른쪽 서브트리로 나뉘는 순간mid = i: i번째 노드는 오른쪽 서브트리의 루트 Index 이다. (Break!!)
- 예시)- sub1 < Root < sub2 = 30 < 50 < 98
- 루트 50(idx=0) < 노드 98(idx=6)
→ 이때 오른쪽 서브트리의 노드는 6번째 원소! =mid=6
→ 왼쪽 서브트리의 노드는 1번째 원소! =start+1
2) 왼쪽 서브트리 탐색
postorder(start+1, mid-1): 왼쪽 서브트리를 계속 탐색하면서 결국 가장 밑에 있는 노드를 발견하게 된다!
3) 오른쪽 서브트리 탐색 : postorder(mid, end)
4) 재귀함수 탈출
mid = end +1: 반복문은range(3, 3)일 때 실행되지 않음으로end+1에 의해, 다음 재귀함수 호출할 때if start > end: return탈출 조건을 만족한다.
5) 왼쪽 서브트리 재귀호출 예시
→ 재귀함수 호출 : start
→ p1(0, 8) → [ p1(1, 5) / p2(6, 8)==오른쪽 서브트리... ]
→ p1(1, 5) → [ p1(2, 4) / p2(5, 5) → <p1(6, 5)p2(6, 5)print(pre[2])> ]
→ p1(2, 4) → [ p1(3, 3) / p2(4, 4) → <p1(5, 4)p2(5, 4)print(pre[4])> ]
→ p1(3, 3) → [ p1(4, 3)p2(4, 3)print(pre[3])
