function solution(w, h) {
[w, h] = w <= h ? [w, h] : [h, w];
let movedDistance, i = 0, cutedSquare = h;
while(i < w){
i++;
movedDistance = h*i/w;
if(!Number.isInteger(movedDistance)) cutedSquare++;
}
return (w*h) - cutedSquare;
}접근
- 대각선은 해당 가로세로의 약수지점에서 격자의 꼭지점에 도달하게되고,
- 꼭지점에 도달할 경우 이동중이던 대각선은 하나의 격자만큼을 덜 자르게된다.
- 한칸씩 이동할때 대각선이 꼭지점에 도달하지 못한경우 +1 을 진행
해설
[w, h] = w <= h ? [w, h] : [h, w];구조분해할당으로 작은 변 w, 큰 변 h
let movedDistance, i = 0, cutedSquare = h;짧은 변의 길이 i, 대각선이 1씩움직일때마다 변화할 movedDistance = 0,
이동할때마다 대각선이 꼭지점에 도달하여 최소한의 격자만큼 잘린경우(정사각형)의 숫자부터 카운트시작 cutedSquare !
while(i < w){
i++;
movedDistance = h*i/w;
if(!Number.isInteger(movedDistance)) cutedSquare++;
}앞서 접근법에따라 i가 작은 변의 길이만큼 1씩 움찍일때
movedDistance가 정수가 아니라면 잘린 사각형의 개수를 ++해준다.
어려웠던 점
h * (i/w)
(h/w) * i
두개의 연산은 완전히 같아 보이지만 다른 결과값을 출력할때가 존재한다.

결국 10진수를 쓰는 우리와는 달리 2진법을 쓰는 컴퓨터는 소수점계산에서
무한소수등의 이유로 소실이 일어나기때문에
위의 연산에서도 다른 결과값이 존재할 수 있다는 것이다.
실제로 풀이과정에서 어려움을 겪은 부분이기도하다.
처음에는 부동소수점 관련하여
테스트케이스가 가로 8 세로 12 였기때문에
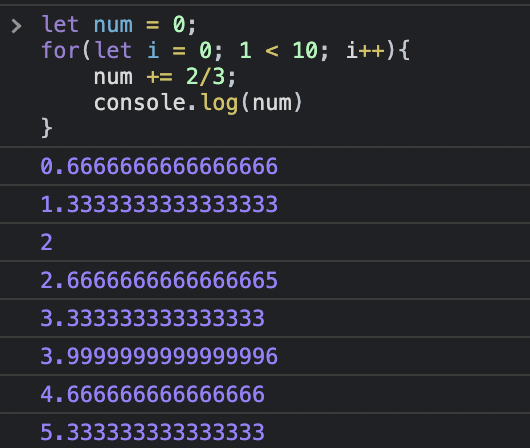
0이라는 숫자에 2/3이라는 숫자를 반복적으로 더해주는데
4가 나와야하는 타이밍에 3.9999999999996이 나와버리는 모습이다.
이때부터는 구현력을 배경지식이 따라가지 못한다고 판단하여
다시 정수부와 소수부의 정밀도를 알아보고 문제풀이를 진행했다.
개선사항
생각보다 코드의 속도가 빠르진 않아서
while문 안에 조건문을 추가시켜서
만약 꼭지점에 도달했고,
해당 가로%i , 세로%i 가 모두 나머지가 0일때(꼭지점도달이 구간의 반복)
이니까 반복되는만큼 더해주고 while문을 종료시킨다는 야심찬 계획!
생각보다 실패케이스가 자꾸 나왔지만 어찌어찌 해결!
먼저 기존의 코드로 실행시킨 속도 !

보충한 뒤 실행시킨 속도 !
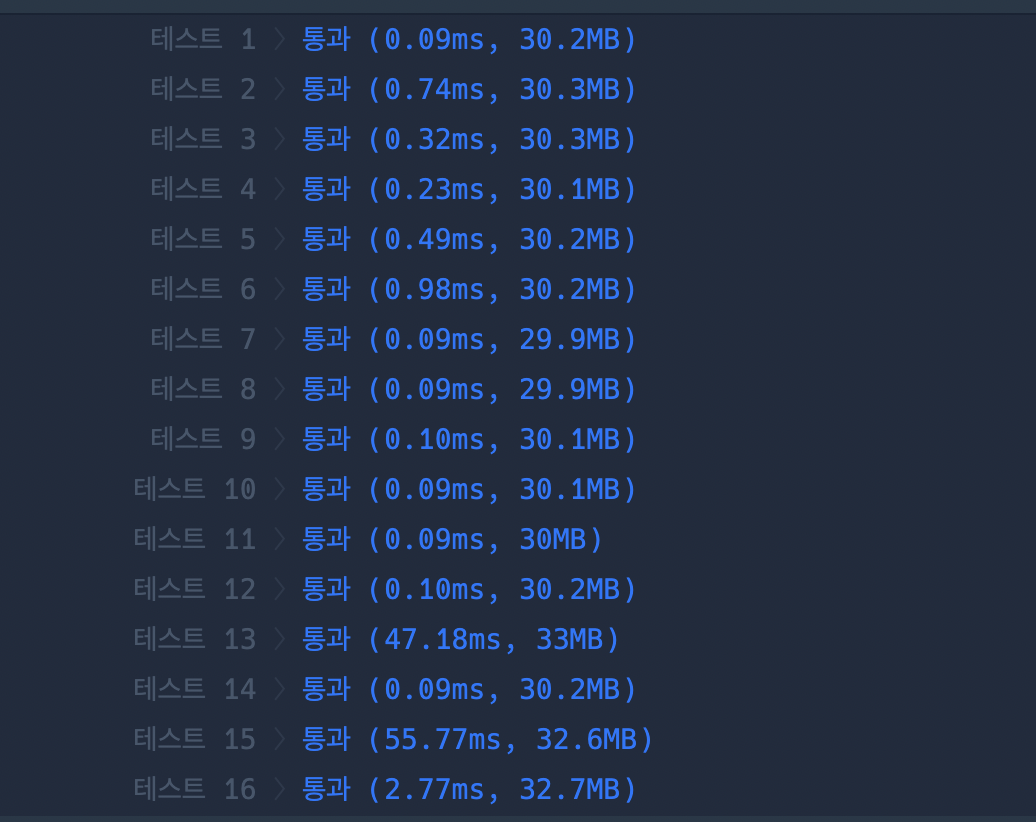
종료조건문의 여부로 테스트케이스12가 364ms에서 0.10ms로 파격적인 변화를 이루었다.
이래도 유클리드호제법으로 최대공약수를 구하고 푼 속도보다 느리지만
풀이과정에서 떠올리지도 못한 방법으로 풀고싶진 않은
조금 고집스런 사람이려나 ?
보충코드
function solution(w, h) {
[w, h] = w <= h ? [w, h] : [h, w];
let movedDistance, i = 0, cutedSquare = h;
while(i < w){
i++;
movedDistance = h*i/w;
if(!Number.isInteger(movedDistance)) cutedSquare++;
else{
if (i === 1) break;
else if (w%i === 0 && h%i === 0 && w !== h) {
cutedSquare += w/i - 1;
break;
}
}
}
return (w*h) - cutedSquare;
}