단일 연결 리스트(Singly Linked List)

각 노드가 데이터와 포인터를 가지고 한 줄로 연결되어 있는 방식으로 데이터를 저장하는 자료구조
다음 노드를 가리키는 포인터는 다음 노드의 주소를 값으로 가지고 있다.

노드의 구성

class Node:
    """링크드 리스트의 노드 클래스"""
    def __init__(self, data):
        self.data = data  # 실제 노드가 저장하는 데이터
        self.next = None  # 다음 노드에 대한 레퍼런스

연결 리스트의 초기화

class LinkedList:
    """링크드 리스트 클래스"""
    def __init__(self):
        self.head = None  # 링크드 리스트의 가장 앞 노드
        self.tail = None  # 링크드 리스트의 가장 뒤 노드

접근

def find_node_index(self, index):
	"""링크드 리스트 접근 연산 메소드""""
	iterator = self.head
    
    for _ in range(index):
    	iterator = iterator.next
    
    return iterator

탐색

가장 앞 노드(head)부터 끝 노드(tail)까지 돌면서 원하는 데이터를 갖는 노드를 리턴

def find_node_data(self, data):
    """링크드 리스트에서 탐색 연산 메소드. 단, 해당 노드가 없으면 None을 리턴한다"""
    node=self.head
    while node is not None:
        if node.data == data:
            return node
        node=node.next

    return None

추가

리스트가 비어 있다면 새로운 노드를 head, tail로 지정
리스트가 비어 있지 않다면 기존의 tail 뒤에 새로운 노드를 추가하고 마지막 노드를 tail로 지정

def append(self, data):
    """링크드 리스트 추가 연산 메소드"""
    new_node = Node(data)
        
    # 링크드 리스트가 비어 있는 경우
    if self.head is None:
        self.head = new_node
        self.tail = new_node
    # 링크드 리스트가 비어 있지 않을 경우
    else:
        self.tail.next = new_node
        self.tail = new_node

삽입

링크드 리스트 가장 앞에 삽입할 경우

def prepend(self, data):
    """링크드 리스트의 가장 앞에 데이터 삽입"""
    new_node=Node(data)
    
    # 링크드 리스트가 비었을 경우
    if (self.head == None):
        self.head=new_node
        self.tail=new_node
    else: # 링크드 리스트에 노드가 있을 경우
        new_node.next=self.head
        self.head=new_node

주어진 노드 뒤에 삽입할 경우

def insert_node(self, pre_node, data):
    """링크드 리스트 주어진 노드 뒤 삽입 연산 메소드"""
    new_node=Node(data)
    
    # 가장 마지막에 삽입
    if pre_node is self.tail:
    	self.tail.next = new_node
        self.tail = new_node
    else: # 두 노드 사이에 삽입
    	new_node.next = pre_node.next
        pre_node.next = new_node

삭제

링크드 리스트 가장 앞 노드를 삭제할 경우
링크드 리스트에 항상 노드가 있다고 가정한다.

def pop_left(self):
    """링크드 리스트의 가장 앞 노드 삭제 메소드"""
    data=self.head.data # 삭제할 노드의 데이터, 확인이 필요한 경우 사용
    
    if self.head.next == self.tail:
       self.tail=None 
    self.head=self.head.next
    
    return data

주어진 노드 뒤 노드를 삭제할 경우

def delete_node(self, pre_node):
	"""링크드 리스트 삭제 연산, 주어진 노드 뒤 노드를 삭제한다."""
    data = pre_node.next.data
    
    # 삭제할 노드가 tail 노드일 경우
    if pre_node.next is self.tail:
    	pre_node.next = None
        self.tail = pre_node
    else: # 두 노드 사이의 노드를 삭제할 경우
    	pre_node.next = pre_node.next.next
    
    return data

시간 복잡도

연산	시간 복잡도
접근	O(n)
탐색	O(n)
삽입	O(1)
삭제	O(1)

현실적인 시간 복잡도

연산	시간 복잡도
접근	O(n)
탐색	O(n)
원하는 노드에 접근 or 탐색 + 삽입	O(n+1)
원하는 노드에 접근 or 탐색 + 삭제	O(n+1)

가장 앞, 뒤에 따른 삽입/삭제 시간 복잡도

연산	시간 복잡도
가장 앞에 접근 + 삽입	O(1+1)
가장 앞에 접근 + 삭제	O(1+1)
가장 뒤에 접근 + 삽입	O(1+1)
tail 노드 전 노드 접근 + 삭제	O(n+1)

head 와 tail 노드는 접근에 O(1)의 시간 복잡도를 가진다.
tail 노드의 전 노드에 접근하는 것은 원하는 노드에 접근하는 것과 같다.

이중 연결 리스트(Doubly Linked List)

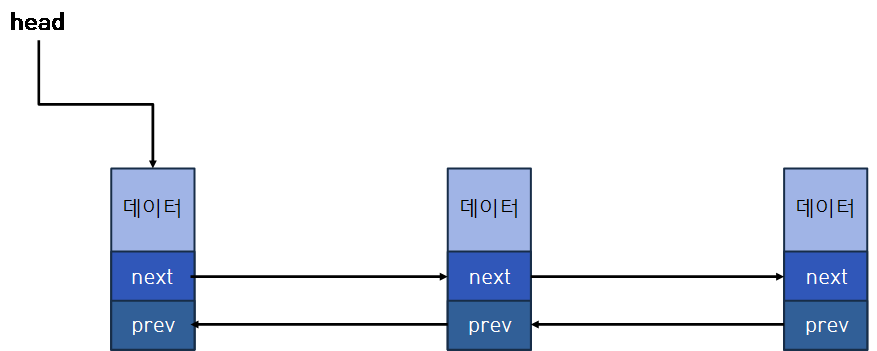
접근 연산, 탐색 연산은 단일 연결 리스트와 동일
next에 더해 이전 리스트를 가리키는 prev에 대한 동작을 추가

삽입

링크드 리스트 가장 앞에 삽입할 경우

def prepend(self, data):
    """링크드 리스트 가장 앞에 데이터를 추가시켜주는 메소드"""
    new_node=Node(data)
    
    # 리스트가 비었을 경우
    if self.head == None:
        self.tail = new_node
    else: # 리스트에 노드가 있을 경우
        new_node.next = self.head
        self.head.prev = new_node
    
    self.head = new_node

주어진 노드 뒤에 삽입할 경우

def insert_after(self, previous_node, data):
    """링크드 리스트 추가 연산 메소드"""
    new_node=Node(data)
    
    # 가장 마지막에 삽입
    if previous_node == self.tail:
        previous_node.next = new_node
        new_node.prev = self.tail
        self.tail=new_node
    else: # 두 노드 사이에 삽입
        new_node.prev = previous_node
        new_node.next = previous_node.next
        previous_node.next.prev=new_node
        previous_node.next=new_node

삭제

def delete(self, node_to_delete):
    """더블리 링크드 리스트 삭제 연산 메소드"""
    data = node_to_delete.data
    
    # 해당 노드를 삭제할 경우 빈 리스트가 되는 경우
    if (self.head == node_to_delete) and (self.tail == node_to_delete):
        self.head = None
        self.tail = None
    # 가장 앞의 노드를 삭제할 경우
    elif self.head == node_to_delete:
        self.head = node_to_delete.next
        self.head.prev = None
    # 가장 뒤에 노드를 삭제할 경우
    elif self.tail == node_to_delete:
        self.tail = node_to_delete.prev
        self.tail.next = None
    else: # 두 노드 사이의 노드를 삭제할 경우
        node_to_delete.prev.next = node_to_delete.next
        node_to_delete.next.prev = node_to_delete.prev
    
    return data    

시간 복잡도

연산	시간 복잡도
접근	O(n)
탐색	O(n)
삽입	O(1)
삭제	O(1)

현실적인 시간 복잡도

연산	시간 복잡도
접근	O(n)
탐색	O(n)
원하는 노드에 접근 or 탐색 + 삽입	O(n+1)
원하는 노드에 접근 or 탐색 + 삭제	O(n+1)

가장 앞, 뒤에 따른 삽입/삭제 시간 복잡도

연산	시간 복잡도
가장 앞에 접근 + 삽입	O(1+1)
가장 앞에 접근 + 삭제	O(1+1)
가장 뒤에 접근 + 삽입	O(1+1)
가장 뒤에 접근 + 삭제	O(1+1)

두 링크드 리스트는 시간 복잡도 면에서 특정한 상황에 대한 차이 외에는 큰 차이가 없음을 알 수 있다.
이중 연결 리스트는 삭제 연산을 할 때 지우려는 노드를 파라미터로 받아 효율적으로 tail 노드를 삭제할 수 있다. tail 노드를 많이 삭제해야하는 상황에서는 이중 연결 리스트를 사용하는 것이 효율적이다.

메모리 면에서는 prev에 대한 데이터가 필요한 이중 연결 리스트보다 단일 연결 리스트가 더 효율적이다.