
특정 구간 내 데이터에 대한 연산(쿼리)을 빠르게 구할 수 있는 트리.
ex) 특정 구간 합,최소값,최대값,평균값 등등
Segment : 부분.분할.나누다.분할하다.
시간복잡도
- 데이터 변경: O(logN)
- 연산: O(logN)
- 데이터 변경할 때마다 M번 연산: O((logN +logN)*M) = O(MlogN)
기본적으로 세그먼트 트리는 이진 트리 구조를 가진다.
즉, 리프 노드가 아닌 모든 노드는 1개 이상, 2개 이하의 자식 노드를 보유한다.
기존 이진 트리에서는 각각의 모든 노드가 고유의 값을 가졌다면, 세그먼트 트리는 부모 노드가 자식 노드들의 합을 저장하는 방식이라고 생각하면 된다.
최상위 루트 노드의 번호는 1번으로 시작하며, 현재 노드가 n 번이라면, 좌측 자식 노드의 번호는 2n 번, 우측 노드의 번호는 2n+1 번이다.
배열로 구현하기 때문에 1번으로 시작해야 더 직관적으로 구분할 수 있어 1번부터 시작한다.
아래는 총 7개의 노드를 가진 세그먼트 트리다.
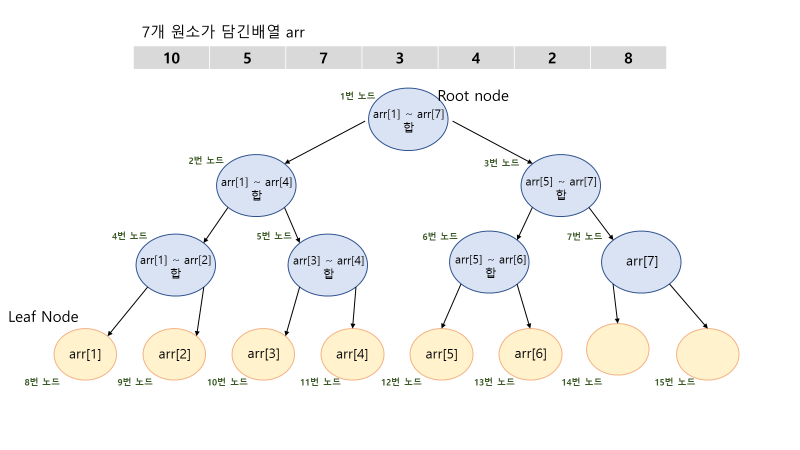
위 그림에서 볼 수 있듯이, 노드가 7개라서 마지막 14, 15번 노드가 비어있지만 2의 제곱 형태라면 모든 노드가 채워지는 완전 이진 트리가 될 수 있다.
전체 필요 노드의 수는 2*n - 1 개이다.
트리의 높이는 루트 노드에서의 가장 긴 경로를 의미한다. 위 그림에서는 높이가 3이다.
n 이 2의 제곱의 개수라면 높이는 log'n' 이다. 노드가 7이라면 2.xxx 겠지만 실제로는 3이므로 log'n' + 1 로 계산하면 된다.
필요한 배열의 크기는 2의 (높이 + 1) 제곱 -1 이다. 남는 위치는 비우면 된다.
=> 근데 귀찮으면 전체 노드 * 4 해주면 충분하다.
JavaScript 는 배열을 초기화 할 때 굳이 사이즈를 지정하지 않아도 자동으로 추가해서 넣어준다.
위 그림에서는 합으로 저장하고 있지만 구간합, 최솟값 모두 가능하다.
전처리도 하고 구간합도 계산 해보자.
const testArr = [10, 5, 7, 3, 4, 2, 8];
const tree = [];
//* 전처리
const preprocess = (start, end, node) => {
if (start === end) return tree[node] = testArr[start];
let mid = Math.floor((start + end) / 2);
let left = preprocess(start, mid, node * 2);
let right = preprocess(mid + 1, end, node * 2 + 1);
return tree[node] = preprocess(start, mid, node * 2) + preprocess(mid + 1, end, node * 2 + 1);
}
preprocess(0, testArr.length - 1, 1);
//* 구간합
const sum = (start, end, node, left, right) => {
if (left > end || right < start) return 0;
if (left <= start && end <= right) return tree[node];
let mid = Math.floor((start + end) / 2);
return sum(start, mid, node * 2, left, right) + sum(mid + 1, end, node * 2 + 1, left, right);
}
//* 0 ~ 2 번 index 까지 합
console.log(sum(0, NODE_COUNT - 1, 1, 0, 2));
//! => 22 출력됨.