[Python] S1_20529_가장 가까운 세 사람의 심리적 거리 🧑👦🧒

https://www.acmicpc.net/problem/20529

문제

여러분은 요즘 유행하는 심리검사인 MBTI에 대해 들어보았는가?

MBTI(Myers-Briggs Type Indicator)는 C.G.Jung의 심리유형론을 근거로 하여 Katharine Cook Briggs와 Isabel Briggs Myers가 보다 쉽고 일상생활에 유용하게 활용할 수 있도록 고안한 자기보고식 성격유형지표이다. (출처: 위키백과)

MBTI는 아래와 같이 네 가지 척도로 사람들의 성격을 구분한다.

• 외향(E) / 내향(I)
• 감각(S) / 직관(N)
• 사고(T) / 감정(F)
• 판단(J) / 인식(P)

각 척도마다 두 가지 분류가 존재하므로, MBTI는 총
$2^4 = 16$가지 유형이 있음을 알 수 있다. 일반적으로 MBTI의 유형들은 각 분류를 나타내는 알파벳 한 글자씩을 따 네 글자로 표시하게 된다. 모든 유형의 목록은 다음과 같다.

• ISTJ, ISFJ, INFJ, INTJ, ISTP, ISFP, INFP, INTP, ESTP, ESFP, ENFP, ENTP, ESTJ, ESFJ, ENFJ, ENTJ

MBTI 성격 유형을 이용하면 두 사람 사이의 심리적인 거리를 정의할 수 있다. 이는 두 사람의 MBTI 유형에서 서로 다른 분류에 속하는 척도의 수로 정의된다. 예를 들어, MBTI 유형이 ISTJ인 사람과 ISFJ인 사람 사이의 거리는 1이며, INTP인 사람과 ENTJ인 사람 사이의 거리는 2이다.

이 정의를 확장해서 세 사람 사이의 심리적인 거리도 정의할 수 있다. 세 사람
$A, B, C$가 있을 때 이들의 심리적인 거리는

• ($A$와 $B$ 사이의 심리적인 거리) + ($B$와 $C$ 사이의 심리적인 거리) + ($A$와 $C$ 사이의 심리적인 거리)

로 정의한다.

대학교에서 심리학 교수로 일하는 종서는 자신이 가르치는 학생들의 심리적인 특성을 분석하고 싶어한다.

오늘이 생일인 종서를 위해
$N$명의 학생들의 MBTI 유형이 주어질 때, 가장 가까운 세 학생 사이의 심리적인 거리를 구해보자.

입력

첫 줄에는 테스트 케이스의 수를 나타내는 정수
$T$가 주어진다.

각 테스트 케이스의 첫 줄에는 학생의 수를 나타내는 하나의 정수
$N$이 주어지며, 두 번째 줄에는 각 학생의 MBTI 성격 유형을 나타내는 문자열들이 사이에 공백을 두고 주어진다.

출력

각 테스트 케이스에 대한 답을 정수 형태로 한 줄에 하나씩 출력한다.

예제

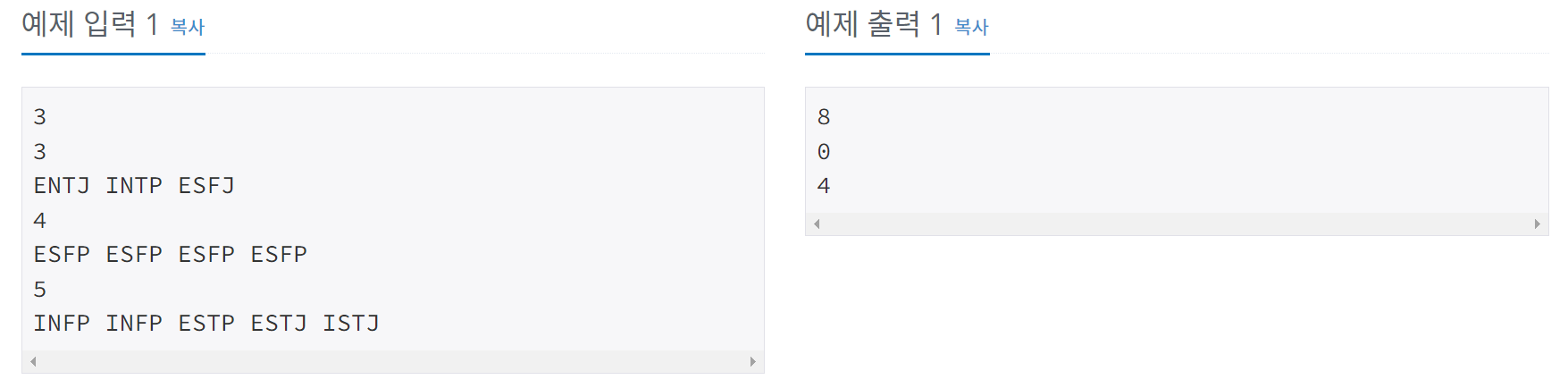
• 첫 번째 테스트 케이스의 경우, ENTJ와 INTP의 심리적인 거리는 $2$, ENTJ와 ESFJ의 심리적인 거리는 $2$, INTP와 ESFJ의 심리적인 거리는 $4$이므로 세 사람의 심리적인 거리는 $2+2+4=8$이다.

• 두 번째 테스트 케이스의 경우, 어떤 사람 둘을 골라도 심리적인 거리가
  $0$이므로 가장 가까운 세 사람의 심리적인 거리는 $0$이다.

• 세 번째 테스트 케이스의 경우, 심리적인 거리를 최소화하려면 MBTI가 ESTP, ESTJ, ISTJ인 세 사람을 골라야 한다. ESTP와 ESTJ의 심리적인 거리는 $1$, ESTP와 ISTJ의 심리적인 거리는 $2$, ESTJ와 ISTJ의 심리적인 거리는 $1$이므로 세 사람의 심리적인 거리는 $1+2+1=4$이다.

조건

• 시간 제한: 2초
• 메모리 제한: 1536MB

코드

import sys
input = sys.stdin.readline

T = int(input())
for _ in range(T):
    N = int(input())
    mbti = list(input().rstrip().split())
    # 비둘기집 원리
    if N > 32:
        print(0)
    else:
        # Brute Force
        minNum = sys.maxsize
        for x in range(N):
            for y in range(N):
                for z in range(N):
                    if x == y or y == z or x == z:
                        continue
                    cnt = 0
                    for i in range(4):
                        if mbti[x][i] != mbti[y][i]: cnt += 1
                        if mbti[x][i] != mbti[z][i]: cnt += 1
                        if mbti[y][i] != mbti[z][i]: cnt += 1
                    minNum = min(minNum,cnt)
                    
        print(minNum)

1. 이 문제는 조금은 생소한 비둘기집 원리를 사용해야 한다.

• 비둘기집 원리란, N+1 마리의 비둘기가 N 개에 상자에 들어간다면, 무조건 1개의 상자에는 2 마리의 비둘기가 들어있다는 것이다.

• 이를 이 문제에 적용시킨다면, MBTI의 가지수는 16 가지이기 때문에, 17 명의 사람이 있다면 무조건 1 명은 누군가와 중복되는 사람이 있다는 것이다.

• 그렇기에 N 이 33 이상이라면, 3 명의 겹치는 사람이 발생하기에 답은 무조건 0 이 나오게 된다.

2. 이를 제외하고는 브루트 포스로 모든 경우를 파악하여 최소값을 구해주면 된다.

느낀 점 & 배운 점

1. 처음에는 이걸 어떻게 풀지.. 무조건 시간초과가 날 것 같았는데 새롭게 알게 된 비둘기집 원리를 사용하니 쉽게 풀 수가 있었다. 이러한 개념은 꼭 외워두어야겠다!