[Leetcode] 169. Majority Element

문제

https://leetcode.com/problems/majority-element/?envType=study-plan-v2&envId=top-100-liked

풀이

시간복잡도 O(N)으로 풀리도록 처음 제출한 풀이는 다음과 같다.

from collections import defaultdict

class Solution:
    def majorityElement(self, nums: List[int]) -> int:
        cnt_dict = defaultdict(int)
        for num in nums:
            cnt_dict[num] += 1
            if cnt_dict[num] > int(len(nums)/2):
                return num

정렬을 이용할 수 있으나 그러면 시간복잡도가 O(NlogN)으로 증가한다.

AC를 받았으나, Follow-up의 이슈(Could you solve the problem in linear time and in O(1) space?)를 해결하기 위해 고민했다.

공간복잡도 O(1)을 만들 수 있는 방법이 도저히 떠오르지 않아 discussion을 보았고, Boyer–Moore majority vote algorithm 를 이용한 풀이가 있었다.

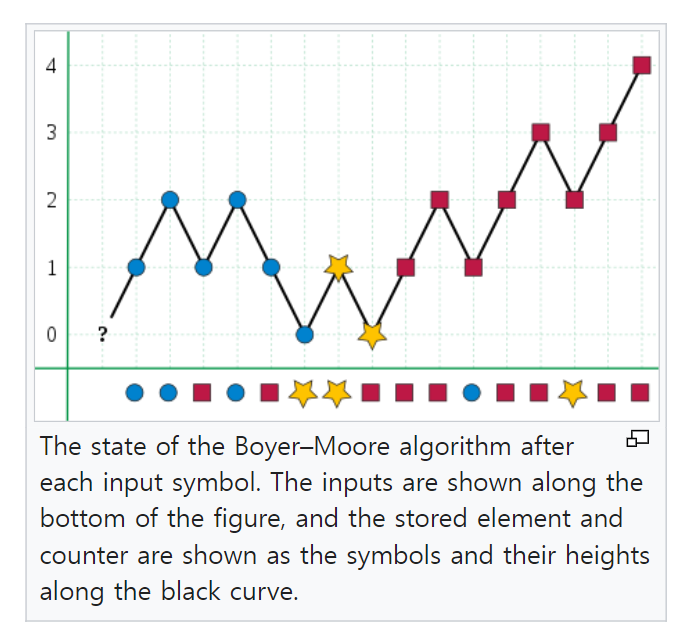
해당 알고리즘은 과반수 원소를 linear time과 constant space를 이용해서 구할 수 있도록 해주는데, 과반수 원소가 존재한다는 전제가 필요하다.

from collections import defaultdict

class Solution:
    def majorityElement(self, nums: List[int]) -> int:
        # Boyer–Moore majority vote algorithm
        count = 0
        candidate = 0

        for num in nums:
            if count == 0: # candidate 탈락
                candidate = num

            if num == candidate: # candidate가 또 등장하면
                count += 1
            else:
                count -= 1
        
        return candidate