[Leetcode] 118. Pascal's Triangle

문제

https://leetcode.com/problems/pascals-triangle/description/?envType=study-plan-v2&envId=top-100-liked

풀이

이전 레벨의 수들을 통해 다음 레벨의 수를 구하면 되었다.(Using Dynamic Programming with 1D Array)
이때 시간복잡도는 O(N^2)이 된다.

class Solution:
    def generate(self, numRows: int) -> List[List[int]]:
        ans = [[1]]
        nums = [1]

        for _ in range(numRows-1):
            new_nums = [nums[0]]
            for i in range(len(nums)-1):
                new_nums.append(nums[i]+nums[i+1])
            new_nums.append(nums[-1])
            
            ans.append(new_nums)
            nums = new_nums
        
        return ans

discussion을 보니 combination 공식을 이용해서 구하는 방법도 있었다. (이 경우 이전 level의 값을 참조할 필요 없다)

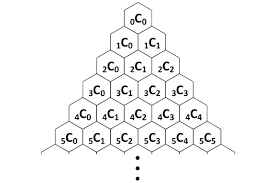
(출처: http://5010.mathed.usu.edu/Fall2015/ARussell/mathematics.html)

class Solution:
    def generate(self, numRows: int) -> List[List[int]]:
        import math

        triangle = []
        
        for n in range(numRows):
            row = []
            for k in range(n+1):
                row.append(math.comb(n, k))
            triangle.append(row)
        
        return triangle

또한, 재귀를 이용한 풀이도 가능하다. 이 경우 같은 레벨에 대해 한번만 계산하므로 시간복잡도는 O(N^2)이다.

class Solution:
    def generate(self, numRows: int) -> List[List[int]]:
        if numRows == 0:
            return []
        if numRows == 1:
            return [[1]]
        
        prevRows = self.generate(numRows - 1)
        newRow = [1] * numRows
        
        for i in range(1, numRows - 1):
            newRow[i] = prevRows[-1][i - 1] + prevRows[-1][i]
        
        prevRows.append(newRow)
        return prevRows