배열에서 K번째 수 찾기 (백준 1300번)

https://www.acmicpc.net/problem/1300

풀이는 다른 블로그에서 너무도 완벽하게 해놨기 때문에 나는 해당 문제에서 내가 얻었던 테크닉이나 생각할 부분들을 위주로 정리를 했다.

• 아이디어 참조

  등차수열에서 특정수 이하의 수 개수를 O(1)으로 찾는 방법을 알아야 하며 탐색하는 대상이 무엇인지를 명확하게 정해야 한다.

• 등차 수열에서 특정수 이하의 개수를 찾는 O(1) 복잡도의 방법

  등차수열의 형태는 i의 배수 형태이다. 각 수열의 원소를 i로 나누면 이들의 위치를 알 수 있다. 따라서 내가 구하고자 하는 수 s를 i로 나눈 몫 보다 작거나 같은 위치를 갖는 수들은 s보다 작거나 같다. 예를들어 등차가 3이고 시작점이 3인 수열에서 7보다 작거나 같은 수는 3 = 1 x 3, 6 = 2 x 3으로 총 7 / 3 = 2개이다.

• 무엇을 찾아야 하는가?

  index가 아니라 실제 수를 찾아야 한다. 따라서 범위는 1~ N * N.

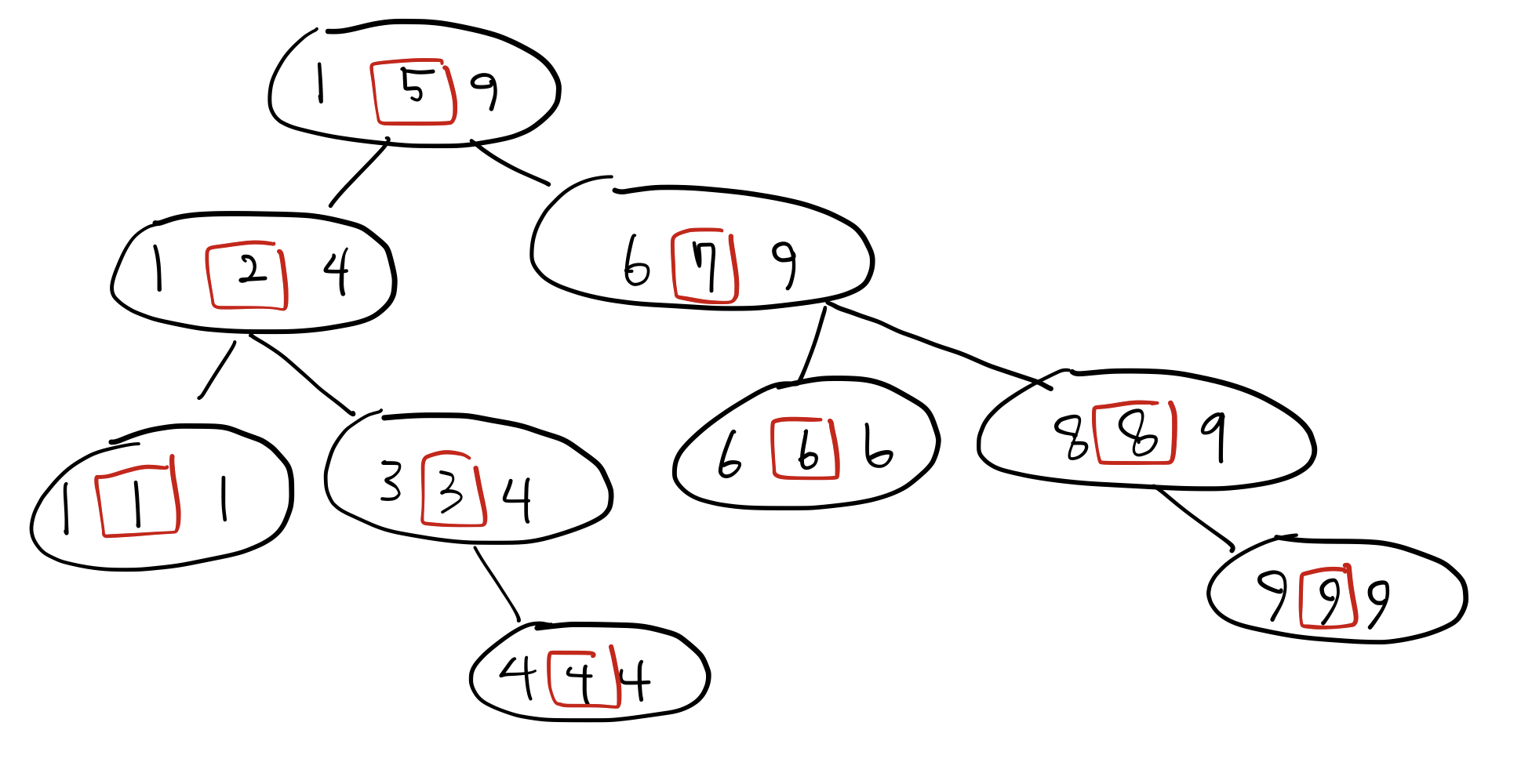
• 하지만 다음과 같은 경우들을 신경써야 한다. ex) 1 2 2 3 3 4 6 6 9 (N = 3).

  • 중간에 5, 7, 8 이 배열에 존재하지 않지만 탐색을 할 때 거쳐 지나갈 수 있다. 이 수들은 이들보다 작고 배열에 존재하는 최대값과 같은 성질을 갖고 있다. n보다 작거나 같은 수의 개수를 c(n)이라고 할 때, c(5) == c(4) 이고 c(6) == c(7) == c(8)이다. 따라서 같은 수가 나왔다고 무작정 break를 하면 틀린다.
  • 등차수열로 정확한 인덱스를 구할 수 있는 경우는 각 숫자 덩어리의 마지막 포지션 뿐이다. 나머지는 추정을 해야 한다. 예를 들어 3번째 인덱스의 2의 경우는 2보다 작거나 같은 수들을 구해서 더할 수 있다. 하지만 2번째 인덱스의 2는 이렇게는 구할 수 없고 추정을 해야 한다. 1 덩어리의 마지막 인덱스보다 크고 2 덩어리의 마지막 인덱스보다는 작으니까 2 겠구나라고 추정을 해야 한다.
  • 결국 해당 문제는 다음과 같이 요약할 수 있다. n보다 작거나 같은 수의 개수를 c(n)이라고 할 때, c(n) >= k를 만족하는 최소 n을 구하는 문제이다.

• 이진 탐색시 주의할 점!

  번호 탐색은 순차적으로 이뤄지지 않는다는 점을 매우 유념하자.
  

• 정답을 지나쳐야 하는 경우도 있다! (바로 덩어리의 끝 지점이 아닐 때)

  반복문은 일단 종료가 될 때까지 돌아야 한다. 그러면 최종 mid값이 정답이 아닐 수도 있다. 정답의 예비 후보를 찾고 이후에 더 그럴듯한 정답이 나오지 않는다면 해당 후보가 정답이 되는 구조다.
  예를 들어서 2번째 인덱스의 2를 찾는다고 가정 했을때 c(2)의 값은 3이 나온다. 이건 찾고자 하는 인덱스 2보다는 크기 때문에 우선 예비 후보로 집어넣고 더 작은 1을 탐색한다. 1의경우는 1로 2보다는 작다. 그리고 반복문은 종료된다.