package baek_1149;

import java.util.Scanner;

public class RGB_plan
{
    public static void main(String args[])
    {
        Scanner sc = new Scanner(System.in);

        int N = sc.nextInt();

        int[][] price_set = new int[N][3];
        int[][] sub_tot = new int[N][3];//특정한 방향으로

        for(int i=0;i<N;i++)
        {
            price_set[i][0] = sc.nextInt();
            price_set[i][1] = sc.nextInt();
            price_set[i][2] = sc.nextInt();
        }

        sub_tot[0][0] = price_set[0][0];
        sub_tot[0][1] = price_set[0][1];
        sub_tot[0][2] = price_set[0][2];

        for(int i=1;i<N;i++)
        {
            //이전값들이 뭔지 살피기만 하면 수열 조건 만족함
            sub_tot[i][0] = price_set[i][0] + Math.min(sub_tot[i-1][1],sub_tot[i-1][2]);
            sub_tot[i][1] = price_set[i][1] + Math.min(sub_tot[i-1][0],sub_tot[i-1][2]);
            sub_tot[i][2] = price_set[i][2] + Math.min(sub_tot[i-1][0],sub_tot[i-1][1]);
        }

        System.out.println(Math.min(sub_tot[N-1][0],Math.min( sub_tot[N-1][1],sub_tot[N-1][2] ) ) );

    }
}

처음 DP문제를 제대로 푼 뒤 느낀점

DP의 메모제이션을 어떻게 적용할지 감이 잡히지 않았다. 하지만 풀이를 접하고 해석하는 과정에서 핵심을 찾았는데 특정 조합까지의 누적합을 메모제이션 하는 개념이었다.

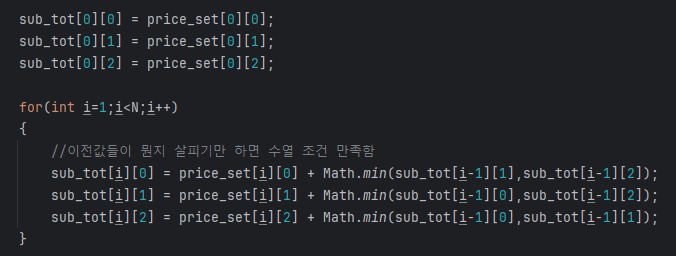
보다싶이 특정번호의 집까지 색칠했을때의 비용을 sub_tot값에 저장해놓는걸 볼 수 있다.
문제 조건에따라서 sub_tot에 어떻게 값을 더할지 정해야 한다. 해당문제 같은경우에는 이웃한 집과 똑같은 색을 색칠하면 안되니 현재 인덱스가 0 이라면 이전인덱스가 1 혹은 2 였던 집의 누적합을 더해준뒤 이번인덱스의 누적합에 저장해준다.

현재(i) 누적합<sub_tot[i]> = 현재(i)의 타겟페인트색비용<price_set[i]> + 이전(i-1)까지의 누적합<sub_tot[i-1]>