영상: CSA2021 컴퓨터시스템구조
강의 소개
-
컴퓨터 공학의 교육과정의 핵심은 컴퓨터 구조, 프로그래밍 언어, 운영체제이다.
-
세 분야의 유사도는 75%로 아주 높으며, 하나라도 놓치면 다른 영역도 이해하기가 매우 어렵다
-
컴퓨터 구조
-
프로그래밍 언어
-
운영체제
제 1장 Part-1
디지털 컴퓨터(Digitial Computer)
-
정의
- 이진 시스템(0,1)을 사용하는 계산을 수행하는 디지털 시스템
- 비트(0과 1의 조합)의 그룹을 사용하여 숫자, 문자 및 기타 정보를 표시하거나 처리
-
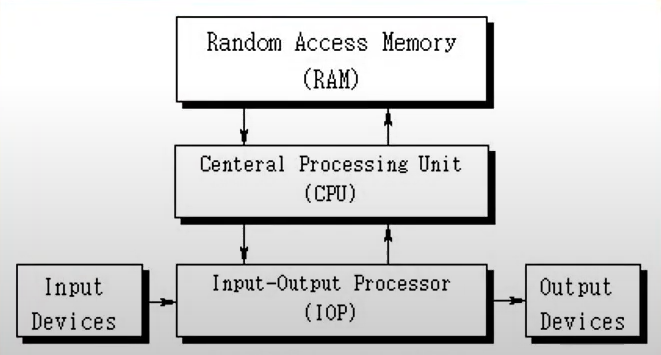
컴퓨터 하드웨어
-
CPU - 중앙처리 장치. 컴퓨터 그 자체로 정의. 산술 논리 처리와 데이터의 저장, 제어 기능 수행
- Centeral Processing Unit
- 컴퓨터 과학에서는 컴퓨터 자체를 CPU로 이야기하는 경우가 많다.
-
주변장치 - 메모리(RAM/ROM), 저장 장치(Storage), 입출력 장치(IO devices)
-
-
컴퓨터 소프트웨어
-
운영체제
- OS- Operating System
-
시스템프로그램
-
유틸리티, 데이터베이스, Editor
- 시스템 프로그램은 운영체제가 만들어질때부터 설계되는 것이기 때문에 MS word나 아래한글은 포함되지 않는다. 응용프로그램에 포함된다.
- Window에서는 노트패드, Unix에서는 Vi를 의미
-
OS에 포함되거나 연결되어 시스템 운영을 보조
-
-
응용 프로그램
- 게임, 웹, MsWord 등
-
-
디지털 컴퓨터의 블럭 구성도
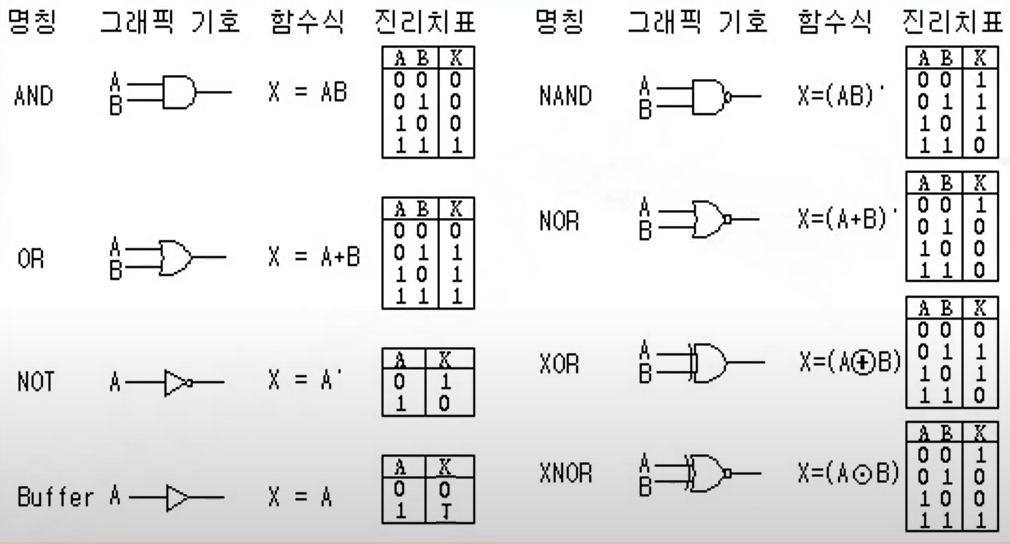
논리 게이트(Logic Gates)
-
명칭 설명
- AND - 둘중 하나라도 0이명 0이다.
- OR - 둘중 하나라도 1이면 1이다.
- NOT - 신호가 들어오면 그 신호의 반대신호를 출력한다.
- Buffer - 들어오는 신호를 출력한다.
- NAND - AND 게이트에 Not을 붙인 것 , AND와 반대의 출력을 보임
- NOR- OR 게이트에 Not을 붙인 것, OR와 반대의 출력을 보임
- XOR - 서로 같은 입력이 들어오면 0 , 서로 다른 입력이 들어오면 1을 출력
- XNOR - 서로 같은 입력이 들어오면 1, 서로 다른 입력이 들어오면 0을 출력
-
이진 정보의 표시
- 0과 1의 전압 신호
- (0V - 5V) 시스템
- (0.5V - 3V) 시스템
-
논리 게이트
- 기본 게이트
- 진리표로 동작 정의
부울 대수(Boolean Algebra)
- 이진 변수와 논리 동작을 취급하는 대수
- 기본 대수 동작 : AND, OR, NOT
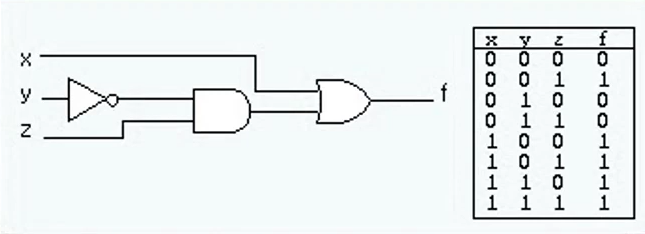
- 부울 대수의 예
- F = x+y`z
- Y에 not을 붙이고 z와 and를 붙인 값을 x와 or시킨다.
- F = x+y`z
-
부울 대수의 사용 이유
- 변수 사이의 진리표 관계를 대수적으로 표시
- 논리도의 입출력 관계를 대수 형식으로 표시
- 같은 기능을 가진 더 간단한 회로의 발견
-
부울 대수의 기본 관계
- 항등원
- 역원
- 교환법칙
- 결합법칙
- 드모르 강의 법칙
-
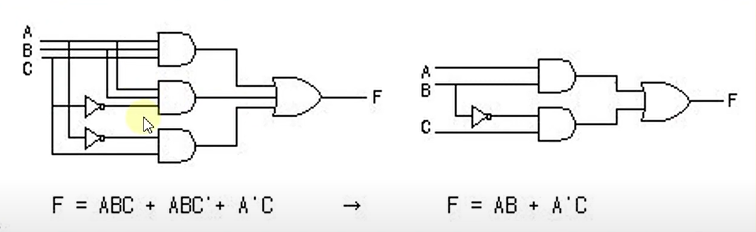
부울 대수의 간략화와 등가 회로
- F = ABC + ABC' + A'C = AB(C+C') + A'C
- 기존 회로는 ABC를 and하고 AB'C를 and하고 A'C를 or했어야한다.
- 하지만 바뀐 회로는
-
부울 대수의 보수
- F = AB + C'D + B'D
- F' = (A'+B')(C+D)(B+D)
맵의 간소화 (Karnaugh Map)
-
부울 함수를 Visual Diagram을 통하여 간소화
-
Karnaugh map, Veitch diagram
-
Minterm, Maxterm을 이용한 간소화
-
논리합의 논리곱
- 1항의 간소화
- 0항의 간소화
-
무정의 조건
- 사용하지 않는 항을 활용하여 간소화
- F=(A,B,C ) = sum(0,2,6)
- d(A,B,C) = sum(1,3,5)
- 사용하지 않는 항을 활용하여 간소화
제 1장 Part-2
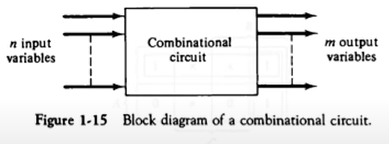
조합회로 (Combinational Circuit)
- 정의
- 입력과 출력을 가진 논리 게이트의 집합
- 출력의 값은 입력의 0,1의 조합에 의하여 결정되는 함수의 결과로 표시
- n개의 입력 조합이 있을 경우 간으한 입력 조합 : 2^n가지
- 조합 회로의 설계 절차
- 해결할 문제의 제시
- 입력과 출력의 변수에 문자 기호 부여
- 입력-출력 관계를 정의하는 진리표 도출
- 어떤 입력이 들어오면 어떤 출력이 나온다
- 각 출력에 대한 간소화된 부울 함수 도출
- 가급적이면 어떤 진리표가 나올 때 카르노맵을 사용해 간단한 부울 수식을 만들면 좋음
- 부울 함수에 대한 논리도 작성
- 논리도를 바탕으로 회로 구현
-
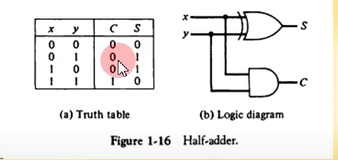
반가산기
- 2개의 비트값을 산술적으로 가산
- S (sum)= x'y + xy' = x xor y
- C(캐리) = xy
- C는 자리 올림수 S 는 합
-
0과 0의 합은 0, carry = 0
-
0과 1의 합은 1, carry = 0
-
1과 0의 합은 1, carry = 0
-
1과 1의 합은 0, carry =1
-
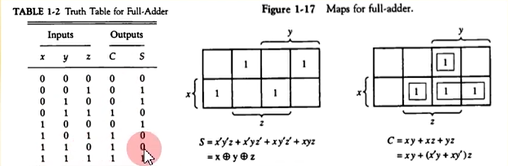
전가산기
- 캐리 값을 포함하여 3비트 가산
- S = x xor y xor z
- C = xy + (x xor y)z
- 캐리 값을 포함하여 3비트 가산
플립플롭 (Flip-Flop)
-
플립플롭의 정의
- 1 비트의 디지털 정보를 저장하는 이진 셀(디지털 메모리)
- 동기식 순차회로의 기본적인 요소로 사용, 조합회로와 함께 순차회로를 구성
- 입력의 상태가 변화를 일으키기 전까지는 이전의 출력상태를 그대로 유지
-
플립플롭의 종류
-
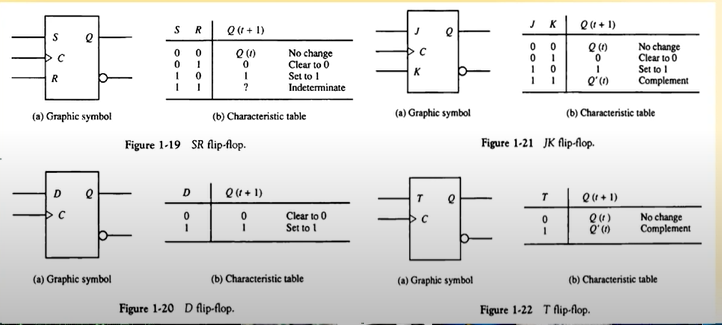
SR-플리플롭
- S값과 R값에 변화가 있더라도 Clock이 들어오기 전까지 Q값의 변화는 없다.
- S와 R 값이 둘다 1인 경우에는 출력값이 정해지지 않는다.
- SR플리플롭은 S와 R이 둘다 1이 되지 않도록 주의할 필요가 있다.
-
D-플리플롭
- D와 Clock이 들어오면 실행되는데, D가 0이면 출력은0, D가1이면 출력은 1
-
JK-플리플롭
- J/K가 둘다 0이면 출력이 그대로 0(SR플리플롭과 동일)
- J/K가 둘다 1이면 현재 Q출력의 반대 출력 즉, Not Q가 출력됨
-
T-플리플롭
- J/K 플리플롭의 단순 형태로, T가 0이면 이전의 값, T가1이면 이전 출력값의 반대를 출력한다.
- 토글 플리플롭이라고도 이야기한다.
-
-
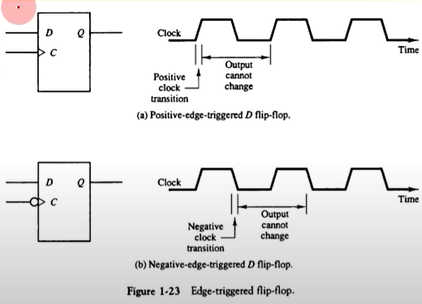
모서리-변이형 플리플롭(Edge-triggered FF)
-
클럭의 동작을 의미
-
입력값의 변화 모서리에서만 동작
- Upward triggered FF
- 입력값이 상향일 경우에만 동작 (0->1)
- Downward triggered FF
- 입력값이 하향일 경우엠나 동작(1->0)
- Upward triggered FF
-
올바른 동작을 위해서는 최소의 신호 유지 시간 필요
- Setup time
- 출력 변화를 위하여 입력이 유지되어야 하는 최소의 시간
- Hold time
- 출력 유지를 위하여 입력이 바뀌지 않아야하는 최소 시간
- Setup time
-
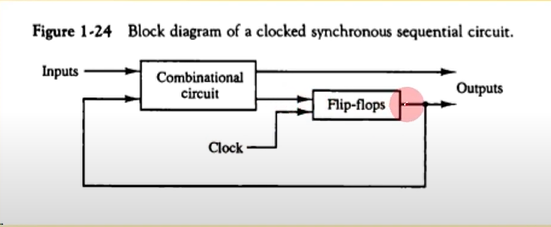
순차회로 (Sequential Circuit)
- 정의
- 플립플롭과 게이트 (또는 조합회로)를 서로 연결한 회로
- 클럭펄스에 의하여 동기화된 입력 순차에 의하여 제어
- 출력은 외부 입력과 플립플롭의 현 상태의 함수로 표시
- 플립플롭의 출력이 그냥 나가는 것이 아니라 다시 조합회로의 입력으로 들어가서 input이 바뀐다 한다고, 반드시 전의 input에 대한 출력이 나오라는 보장은 없다.
-
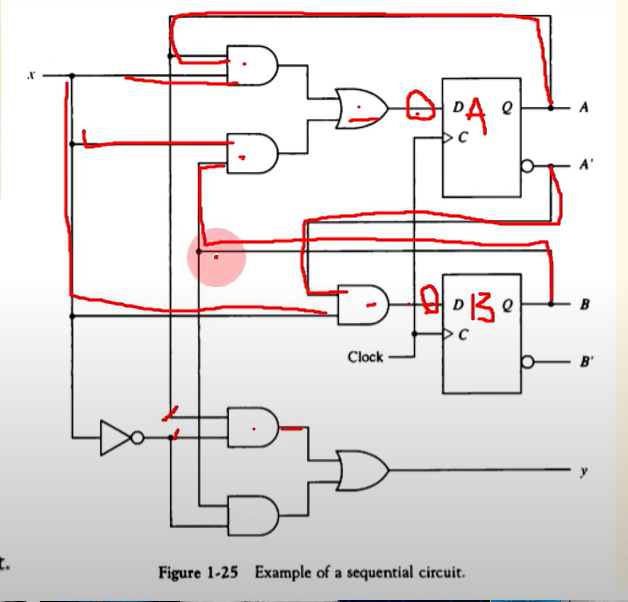
플립플롭의 입력식
-
FF의 입력을 만들어내는 조합 회로 부분
-
부울 수식에 의하여 표현
-
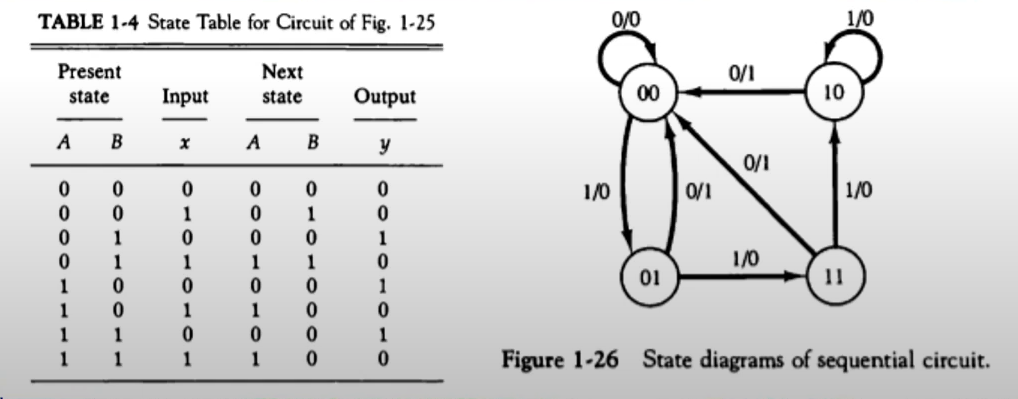
상태표(State Table)
-
-
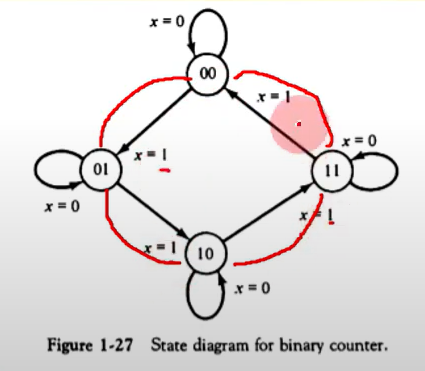
상태도(State Diagram)
- DA = Ax + Bx
- DB = A'X
- y = AX' + BX'
-
순차회로 설계
-
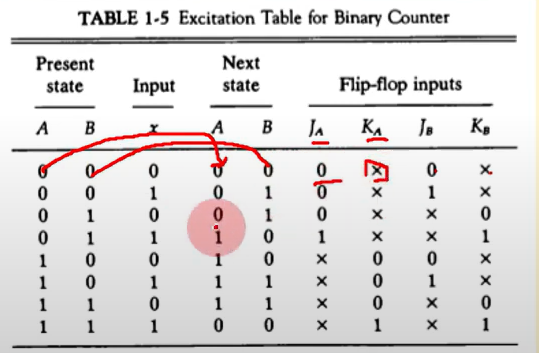
2비트 2진카운터의 설게
- 상태표, 상태도 작성
-
2. 순차회로 여기표 작성
3. 플립플롭의 선택과 입력식 도출
4. 회로도 구현