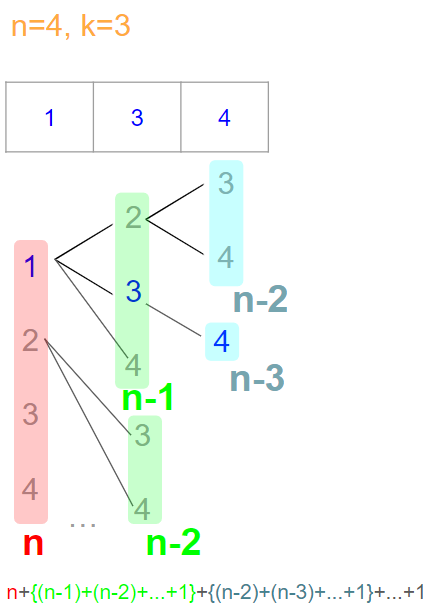
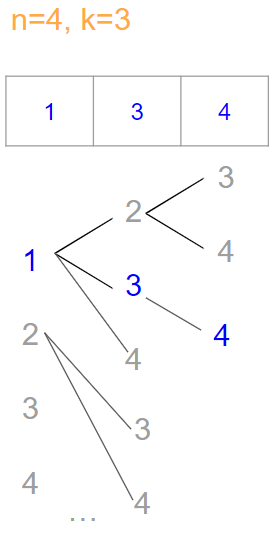
Intuition

모든 조합의 경우의 수를 확인하기 위해 재귀로 접근한다.

Approach

Leetcode의 2차원 배열 반환

본격적으로 시작하기에 앞서 leetcode에서 2차원 배열을 반환받는 방식이 조금 특이하기에 이것부터 짚고 넘어가야한다.
skeleton code에 int* returnSize와 int** returnColumnSize가 있는 것을 볼 수 있다.
각각은 number of rows와 number of columns 즉, 모든 조합의 경우의 수와 k를 의미한다.

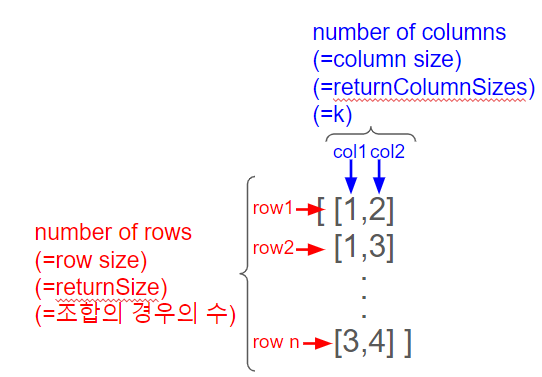
그런데 좀 특이한 것이, 이러한 방식을 다른 문제에서도 적용하기 위해서인지 columnSize의 경우는 1차원 배열에 각각의 row마다 columnSize가 몇인지 적어줘야한다.

//k=2일 경우 returnColumnSize배열의 모습
[2,2, ... 2]

이 부분에서 내가 들었던 의문은 왜 returnColumnSize에 asterisk두 개가 붙어 있냐는 것이었다. 아마 추정컨대, main함수에서는 정수형 포인터였을 것이고, 이것이 combine함수에서는 어떤 정수가 담길 것이 아니라 정수배열이 담겨야하기 때문에 이중 포인터로 인자를 넘겼을 것이다.

본격적 문제 풀이

이제 number of rows 즉, 조합의 경우의 수를 구해 returnSize부터 값을 할당시켜주겠다.
조합의 수를 구하기 위해 팩토리얼을 계산하는 것은 문제의 조건상 가능하긴하지만, n이 커져도 작동하는 파스칼의 삼각형을 이용했다.

int pascal(n,k){
    if (k==1) return n;
    if (n==k) return 1;
    return pascal(n-1,k-1)+pascal(n-1,k);
}
int** combine(int n, int k, int* returnSize, int** returnColumnSizes) {
    *returnSize=pascal(n,k);
    ...

returnColumnSize는 returnSize만큼 배열을 malloc한 다음 모두 k를 할당시켜준다.

    *returnColumnSizes=(int*)malloc(sizeof(int)*(*returnSize));
    for (int i=0;i<(*returnSize);i++) (*returnColumnSizes)[i]=k;

이제 본격적으로 조합들을 만들어 보겠다.
각각의 경우의 수는 임시 배열에 담겨있다가 하나가 완성될때마다 최종 배열로 옮겨 담는 방식으로 작동된다.

int** res;
int* tmp;
int resIdx;
void cases(int n, int k, int preNum, int tmpIdx){
    if (tmpIdx==k){
        for (int i=0;i<k;i++) res[resIdx][i]=tmp[i];
        resIdx++;
    }
    else{
    ...
    }
}
...
int** combine(int n, int k, int* returnSize, int** returnColumnSizes) {
    ...
    resIdx=0;
    tmp=(int*)malloc(sizeof(int)*k);
    cases(n,k,1,0);
    free(tmp);
    return res;
}

한 번 사용된 원소는 재등장 할 수 없기 때문에 이전 함수에서 호출되었던 i보다 +1한 인덱스부터 인자를 호출하도록 설계하였다.

void cases(int n, int k, int preNum, int tmpIdx){
    if (tmpIdx==k){
        for (int i=0;i<k;i++) res[resIdx][i]=tmp[i];
        resIdx++;
    }
    else{
        for (int i=preNum;i<=n;i++){
            tmp[tmpIdx]=i;
            cases(n,k,i+1,tmpIdx+1);
        }
    }
}

Solution

/**
 * Return an array of arrays of size *returnSize.
 * The sizes of the arrays are returned as *returnColumnSizes array.
 * Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
 */

#include <stdlib.h>
int** res;
int* tmp;
int resIdx;

void cases(int n, int k, int preNum, int tmpIdx){
    if (tmpIdx==k){
        for (int i=0;i<k;i++) res[resIdx][i]=tmp[i];
        resIdx++;
    }
    else{
        for (int i=preNum;i<=n;i++){
            tmp[tmpIdx]=i;
            cases(n,k,i+1,tmpIdx+1);
        }
    }
}

int pascal(n,k){
    if (k==1) return n;
    if (n==k) return 1;
    return pascal(n-1,k-1)+pascal(n-1,k);
}

int** combine(int n, int k, int* returnSize, int** returnColumnSizes) {
    *returnSize=pascal(n,k);
    *returnColumnSizes=(int*)malloc(sizeof(int)*(*returnSize));
    for (int i=0;i<(*returnSize);i++) (*returnColumnSizes)[i]=k;

    res=(int**)malloc(sizeof(int*)*(*returnSize));
    for (int i=0;i<(*returnSize);i++) res[i]=(int*)malloc(sizeof(int)*k);

    resIdx=0;
    tmp=(int*)malloc(sizeof(int)*k);
    cases(n,k,1,0);
    free(tmp);

    return res;
}

Complexity

Time Complexity

$\therefore O(N^2)$