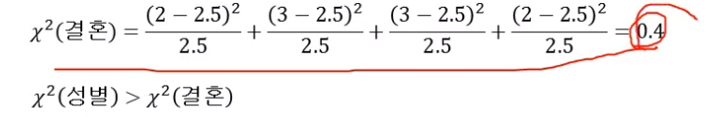
의사결정나무 = 분류나무 + 회귀나무
의사결정나무
- 목표 : 예측변수(=독립변수)를 기반으로 결과를 분류하거나 예측
- 의사결정규칙(decision rule)을 나무구조(tree)로 도표화하여 분류(classification)와 예측(prediction)을 수행하는 분석방법
ex) 은행 고객 대출 제안 수락여부
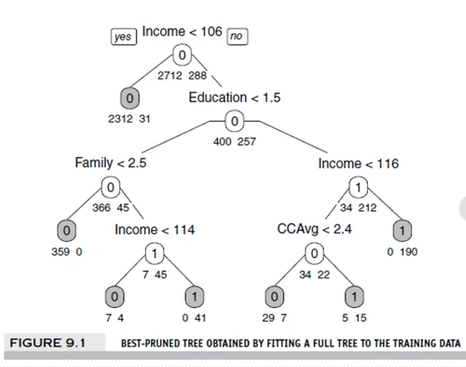
목표: 어느 고객이 대출 제안을 수락(yes)/거절(no)할 지를 분류
규칙:
IF (Icome >=106) <- 이 사람이 대출을 할지 말지 결정하는 가장 중요한 변수를 루트 변수로
AND (Education < 1.5)
AND (Family <= 2.5)
주요 방법
-
Trees and Rules 구조
- 규칙(Rules)은 나무모델(tree diagrams)로 표현
- 결과는 규칙(rules)으로 표현
-
재귀적 분할(Recursive partitioning)
- 나무 만드는 과정
- 그룹이 최대한 동질 하도록 반복적으로 레코드를 하위 그룹으로 분리
ex) yes / no로 나눠질 때까지
-
가지치기(Purning the tree)
- 생성된 나무를 자르는 과정(정교화)
- 과적합을 피하여 위해 필요 없는 가지를 간단히 정리
뿌리노드, 부모노드, 자식노드
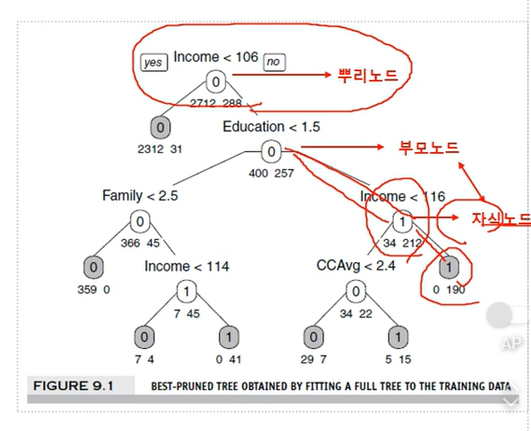
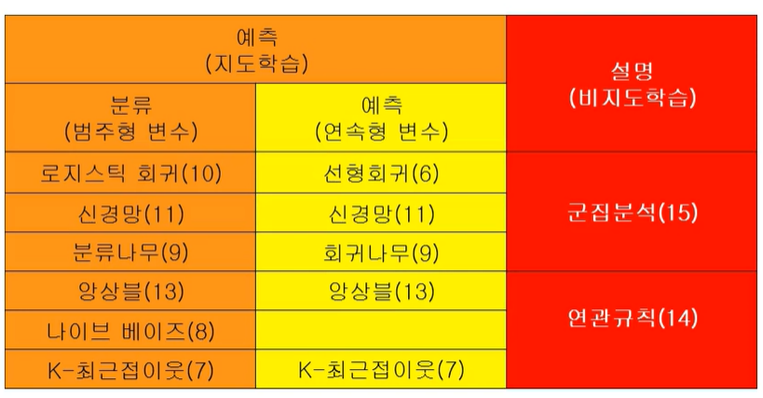
의사결정나무 구분
구분
- 분류나무 (Classificaiton Tree) : 목표 변수가 범주형 변수 -> 분류
- 회귀나무 (Regression Tree) : 목표 변수가 수치형 변수 -> 예측
재귀적 분할 알고리즘
- CART(Classification And Regression Tree)
- C4.5 -> C5.0
- CHAID (Chi-square Automatic Interaction Detection)
불순도(Impurity)알고리즘
- 지니 지수(Gini index)
- 엔트로피 지수(Entropy index), 정보 이익(Informaiton Gain)
- 카이제곱 통계량(Chi-Square statistic)
불순도란 하나의 그룹을 만들었을 때, yes와 no가 몇 개씩 있는지 계산
분류나무(Classification Tree)
-
목표변수: 범주형 변수(분리)
-
분류 알고리즘과 불순수도 지표
- CART : 지니 지수(Gini index)
- C4.5 : 엔트로피(Entropy index), 정보이익(Information gain), 정보이익비율(Information gain ratio)
- CHAID : 카이제곱 통계량(Chi-Square statistic)
-
끝마디: 소속집단
-
경향(랭킹)도 가능
왼쪽 끝마디 Nonowner가 7이니깐, 그 마디는 Nonowner그룹이다.
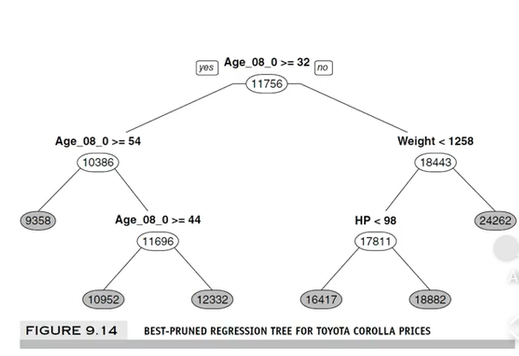
회귀나무(Regression Tree)
- 목표변수 : 수치형 변수 (예측)
- CART: F 통계량 - 분산의 감소량
- 끝마디 : 집단의 평균
- 예측일 경우 회귀나무보다 신경망 또는 회귀분석이 더 좋음
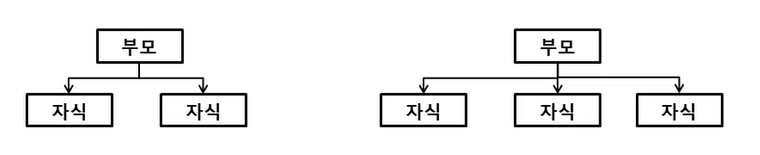
의사결정나무 분리기준
분리
- 이지분리(binary split) : CART
- 다지분리(multi-way split) : CHAID, C4.5, C5.0, ...
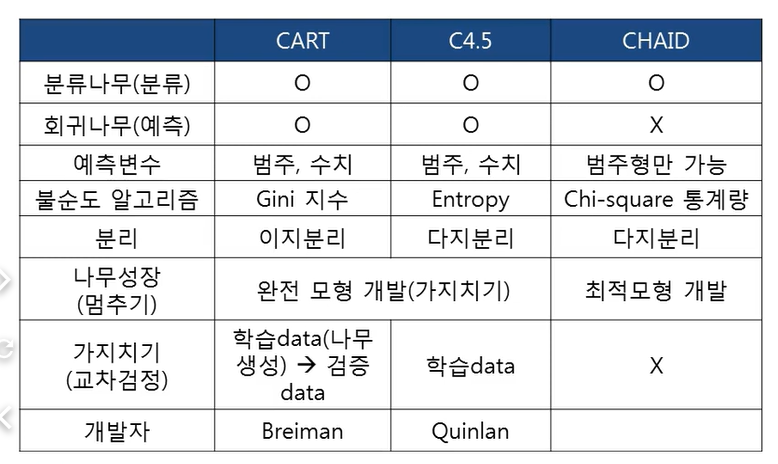
CART(Classification And Regreession Tree)
- Breiman 등이 개발
- 종류: 분류나무, 회귀나무 가능
- 불순도 알고리즘: Gini 지수(Gini Index) - 불확실성 (↓) or (↑)
- 분리: 이지분리(binary split)
- 가지치기(교차 타당도): 학습 데이터를 이용하여 나무를 성장시키고, 데이터를 이용하여 가지치기
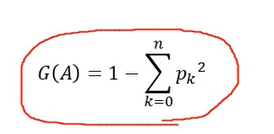
- 2번 복원 추출했을 때 나올 수 있는 확률
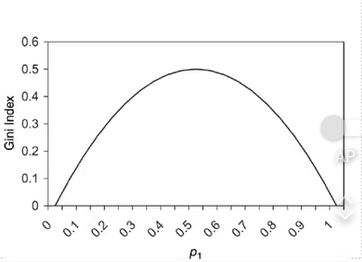
- 최대 G(A) = 0.5(두 집단이 동일 할 때)
- 그룹의 class가 동일하면 지니지수 ↓
- 그룹의 class가 다양하면 지니지수 ↑
예제
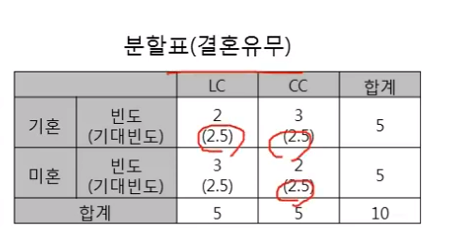
- 우리 홈쇼핑에서는 충성고객(LC: Loyal Customer)와 탈퇴고객(CC: Churn Customer)을 구분하는 규칙을 생성하고자 함)
- 총 10명의 고객을 대상으로 성별과 결혼유무 중 어느 변수가 더 분류를 잘하는 변수인지 찾고, 분류규칙을 찾고자 함
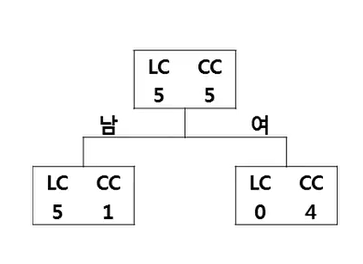
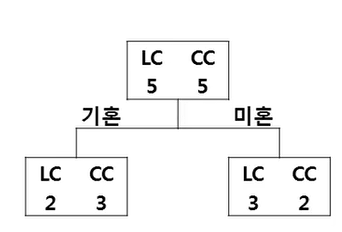
=> 성별이 class를 더 잘 분류해준다
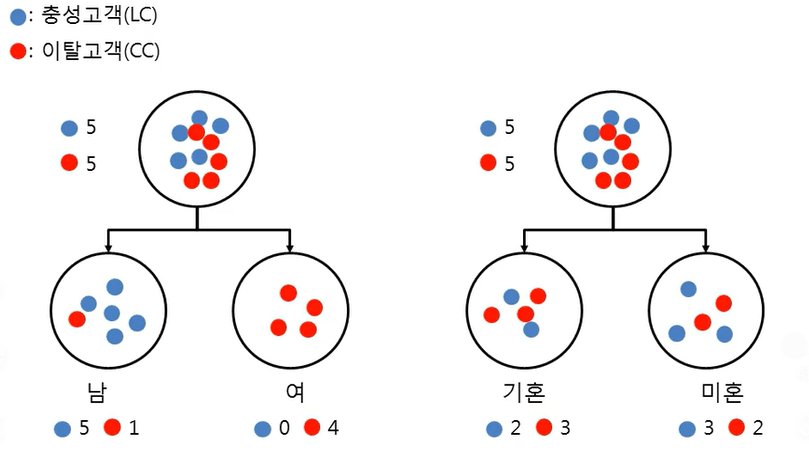 왼쪽은 성별로 가지를 분류, 오른쪽은 결혼 여부로 가지를 분류
왼쪽은 성별로 가지를 분류, 오른쪽은 결혼 여부로 가지를 분류
성별에 따른 Gini index

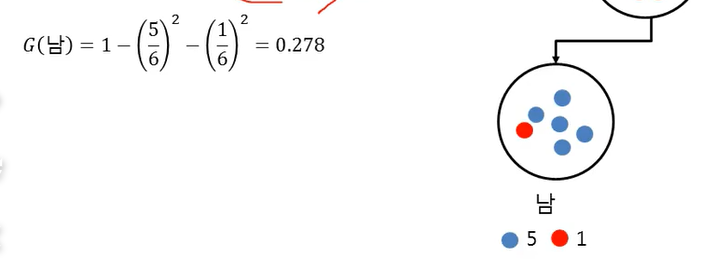
 -> 지니 지수 0: 다 맞췄다는 뜻
-> 지니 지수 0: 다 맞췄다는 뜻
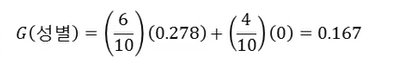 -> 가중치: 6/10, 4/10
-> 가중치: 6/10, 4/10
=> 0.5에서 0.16만큼 줄었음 = 불확실성 크게 줄었다.
어떤 변수를 선택?
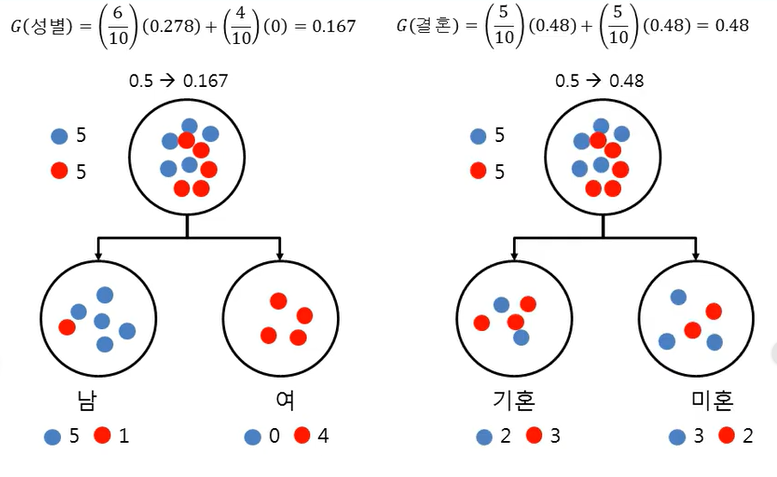
=> 성별을 선택
C4.5
- Quinlan이 개발
- 종류: 분류나무, 회귀나무 가능
- 불순도 알고리즘: 엔트로피(Entropy), Information gain, 이득율(gain ratio)
- 분리: 다지분리
- 가지치기(교차 타당도): 학습데이터만 이용하여 나무를 성장 및 가지치기
- 정보이론(엔트로피): 밑이 2인 log로 계산하는 이유 -> bit 수로 정보 계산
- log로 계산하는 이유 : 대부분 분수로 나옴
- IG: 정보이익 = 정보의 가치 (↓) or (↑)
E(before) : 사전 불확실성, E(After): 사후 불확실성
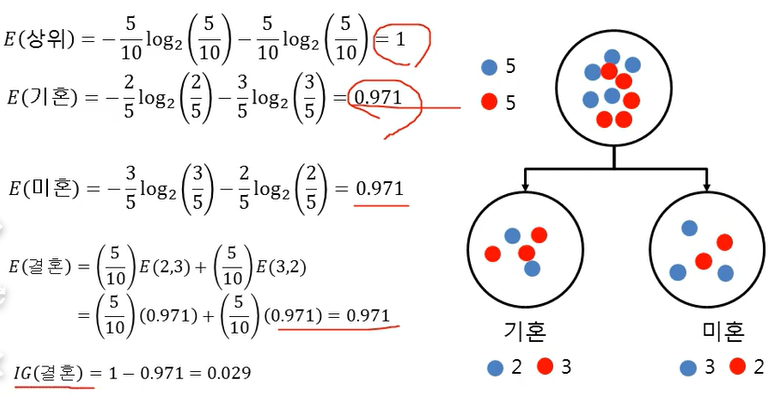
예제
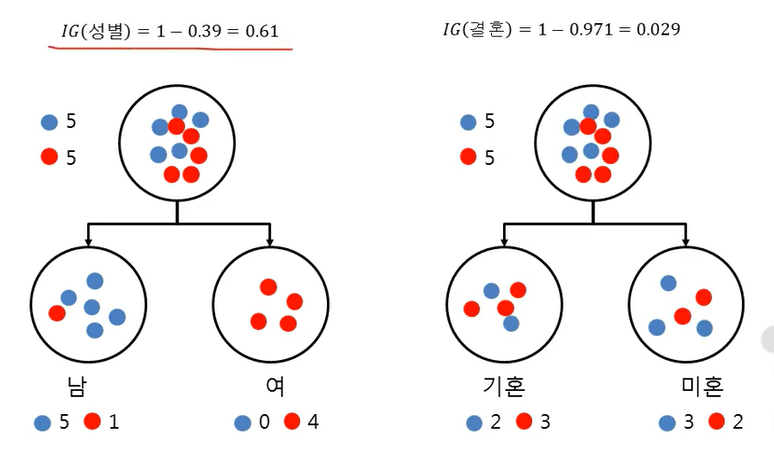
성별에 따른 Entropy
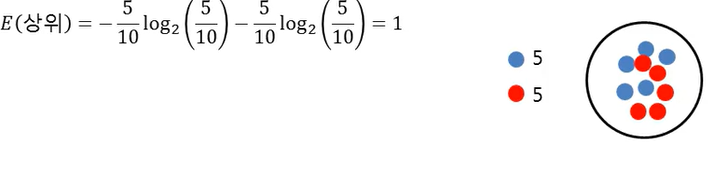
=> 엔트로피는 아무것도 구분 못했을 때 1이 나옴
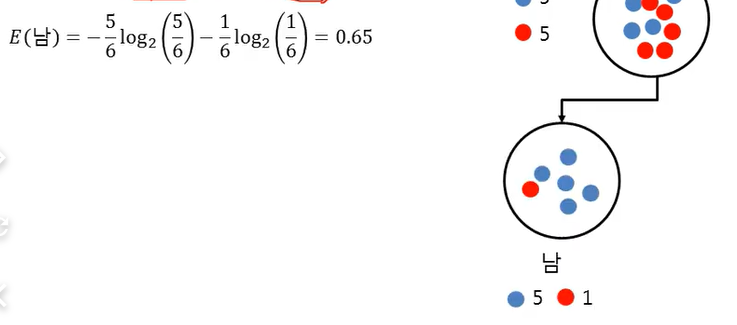
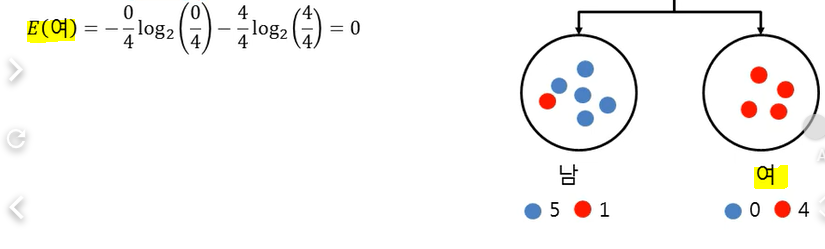

결혼에 따른 Entropy
어떤 변수를 선택?
이득률(Information gain ratio)
- C4.5에서는 informaiton gain → information gain ratio
- 가지가 많은 경우에 information gain이 높은 경향 (가지 많은 쪽을 선택하게 된다)
- IV(Intrinsic value)를 이용하여 정규화
- IV(Intrinsic value)를 이용하여 정규화
- 가지가 많으면 감점 부여
- 이득률
Information gain ratio

CHAID
- 목적: 분류나무만 가능
- 불순도 알고리즘: Chi-squre 통계량, F통계량 이용
- 분리: 다지분리
- 가지치기 없음: 나무 성장에만 활용하여 Stop규칙 적용
- 입력변수와 목표변수가 모두 범주형만 가능

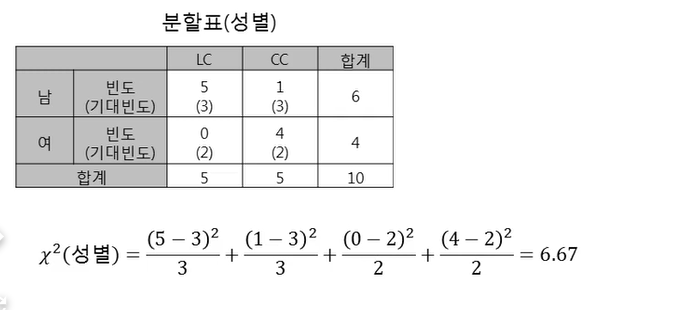
LC : CC = 1: 1이기 때문에 남자 LC,CC 각각 3명(괄호 값)들어가야한다.(이론적으로)
분자의 (5-3)2 → 원래 이론적으로 3개인데, 얼마만큼 구분해주는가