지난 글 hjee02018.log - Greedy 활용 ② 에 이어 Greedy를 활용한 문제 풀이를 해보도록 한다.
1. 문제 개요
1) 문제 정의

- 모든 정점(섬)을 연결하는 다리의 최소 건설 비용을 구할 것
2) 제한 사항
위 문제의 경우 별다른 제한 사항이라기 보다 다음의 것을 고려하여 문제 풀이를 하면 된다.
① 중복된 연결은 주어지지 않는다.
- {1,2,4}와 {2,1,4}는 같은 다리이므로 한 번만 주어진다.
② 연결할 수 없는 섬은 주어지지 않는다.
③ costs(연결할 수 있는 다리의 연결 비용)은 최대 값((n-1)*n)/2 을 초과하지 않는다.
3) 입출력 형식
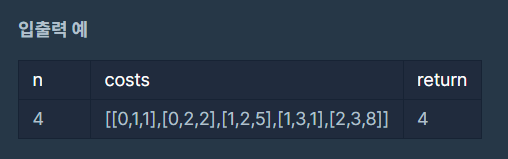
위 예시를 도식화하면 다음과 같다.
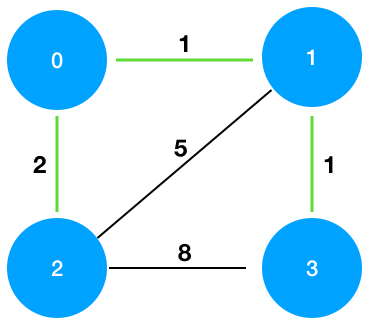
=> 모든 섬(정점)을 연결하는 최소 다리 건설 비용은 4(2+1+1) 이다.
2. Solution I.
1) 주요 알고리즘
① 연결된 섬 저장
#include <string>
#include <vector>
#include <map>
#include <unordered_set>
#include <algorithm>
#include <iostream>
using namespace std;
int solution(int n, vector<vector<int>> costs)
{
int answer = 0;
// 다리 연결 여부
map<int, vector<int>> cn;
// 다리 건설 비용
map<pair<int, int>, int> p;
for (int i = 0;i < costs.size();i++)
{
int a, b, cost;
a = costs[i][0];
b = costs[i][1];
cost = costs[i][2];
// cn에 연결된 섬을 저장
cn[a].push_back(b);
cn[b].push_back(a);
p[{a, b}] = cost;
p[{b, a}] = cost;
}
② 연결할 섬의 시작점을 임의로 선택한 후 연결된 섬 중 건설비용이 최소인 다리를 건설
while (cnt < n)
{
if (cn.empty())
break;
// 번호순 정렬이 아니라 최솟값(건설비용) 정렬
//sort(cn[cur].begin(), cn[cur].end());
int idx=-1;
int min=999999;
for (int i = 0;i < cn[cur].size();i++)
{
if (p[{cur, cn[cur][i]}] < min &&isvisited[cn[cur][i]]==false)
{
min = p[{cur, cn[cur][i]}];
idx = cn[cur][i];
}
}
if (idx == -1)
break;
int next = idx;
isvisited[next] = true;
price += p[{cur, next}];
cur = next;
cnt++;
}③ 모든 섬을 연결하였다면 종료
if (cnt == n)
if (answer == 0)
answer = price;
else
answer = min(price, answer);
}
위 코드 실행 시 정확도 테스트를 통과하지 못한다.
위 코드의 오류는 다음의 사실을 배제한 알고리즘이라는 점이다.
- 하나의 섬에서 연결되는 다리의 수는 1개를 초과할 수 있다.
3. Solution II.
위 문제를 풀기 위해 가장 먼저 떠올려야하는 것은 MST(Minimum Spanning Tree, 최소 신장 트리)이다. 최소 신장 트리를 통해 크루스칼 알고리즘을 구현하고 최소 건설 비용을 탐색할 수 있다.
1) 알고리즘 (Kruskal Algorithm)
그래프 내의 모든 정점을 가장 적은 비용으로 연결하기 위해 사용하는 알고리즘. 여기서 그래프란 무방향 그래프로 정점과 간선으로 구성되며, 간선은 비용과 같은 가중치를 포함한다.
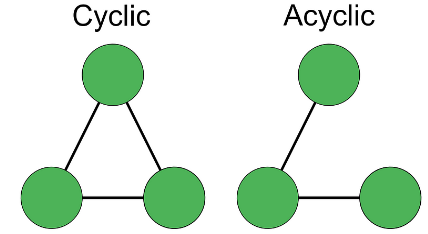
신장 트리란?
: 그래프에서 모든 정점을 포함하고 정점간 서로 연결되며 acyclic한 그래프.
- acyclic 이란? | cycle이 존재하지 않는 그래프.
최소 신장 트리란?
: 신장 트리 중 최소 비용(가중치의 합이 최소)을 가지는 트리이다.
최소 신장 트리를 구하기 위한 크루스칼 알고리즘은 다음과 같다.
① 그래프의 간선을 가중치 기준 오름차순 정렬
#include <string>
#include <vector>
#include <algorithm>
using namespace std;
bool cmp(vector<int>a, vector<int>b)
{
return a[2]<b[2];
}
int solution(int n, vector<vector<int>> costs)
{
int answer = 0;
sort(costs.begin(),costs.end(),cmp);② 가중치(건설 비용)가 가장 작은 간선을 선택
bool visited[101] = { false, };
int solution(int n, vector<vector<int>> costs)
{
// ... ① 과정 생략
visited[costs[0][0]]=true;
visited[costs[0][1]]=true;
answer+= costs[0][2];
}③ 모든 노드가 연결될 때까지 위 과정을 반복한다.
// ②과정에서 연결된 노드(2개)
int count=2;
while(1)
{
for(int i=1;i<costs.size();i++)
{
// 이미 모든 섬이 연결되었다면 break;
if(cnt==n)
break;
// 두 섬을 연결하는 다리가 이미 존재하지 않을 때에만(XOR),
if(visited[costs[i][0]] != visited[costs[i][1]] )
{
visited[costs[i][0]]=true;
visited[costs[i][1]]=true;
answer+=costs[i][2];
count++;
break;
}
}
// 모든 노드가 연결되었다면 비용을 반환하며 반복문을 종료
if(count==n)
break;
}
Kruskal 알고리즘은 가중치 기준 간선 정렬, 최소 가중치 간선 선택, 사이클 검사를 반복하며 모든 정점니 MST에 포함될 때까지 수행한다. 이 알고리즘은 각 단계마다 최적의 선택(최소 가중치 선택)을 함으로써 전체 그래프의 MST를 형성하므로 Greedy 알고리즘의 일종으로 사용된다.
MST를 구하는 Kruskal 알고리즘 또한 자주 활용된다. 다음 게시글에서 네트워크 분할 문제와 비교하여 Greedy를 더 깊이있게 이해해보고자 한다.