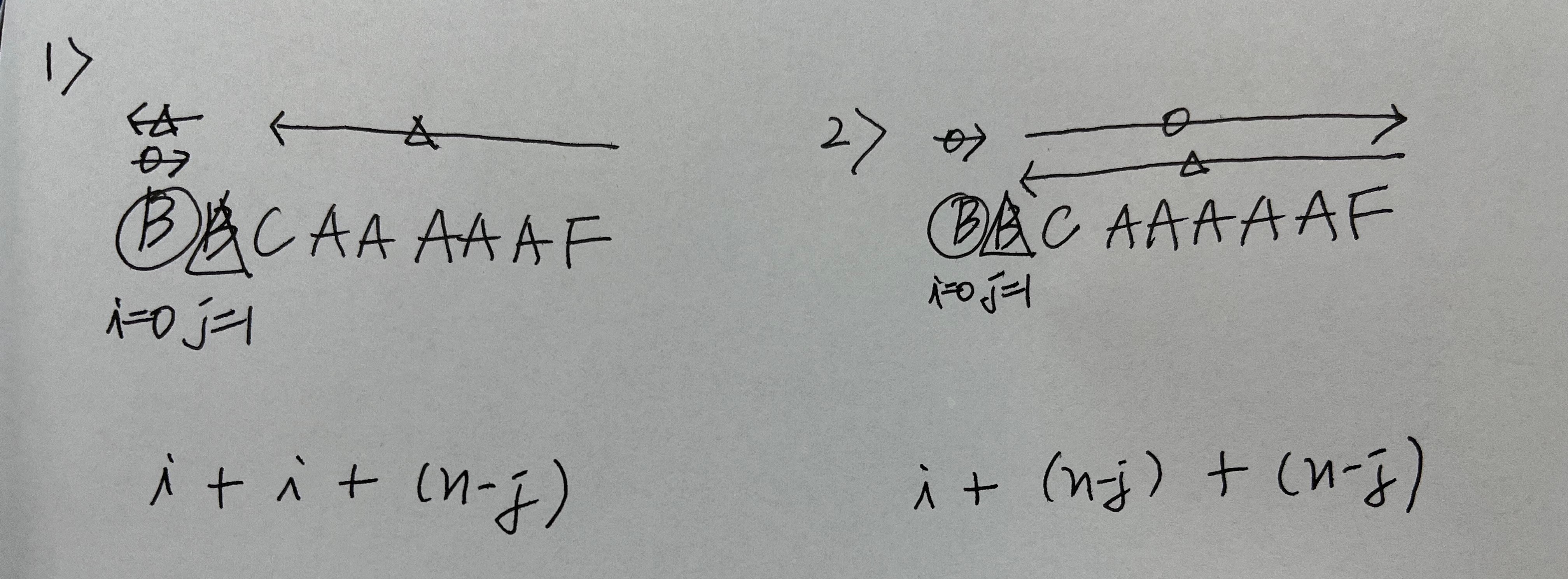1. Greedy 알고리즘이란?
문제 해결의 각 단계에서 최선의 선택을 함으로써 전체 문제에 있어서 최적의 해를 찾는 것. 즉, 각 단계 별 최선의 선택을 계쏙 진행하여 전역적으로 최적의 해를 찾고자 한다.
Greedy 알고리즘은 비교적 간단하게 적용되지만, 항상 최적의 해를 보장하는 것은 아니다.
1) 문제 해결 과정
Greedy 알고리즘을 적용한 일반적인 문제 해결 과정은 다음과 같다.
① 문제 정의
: 문제를 정의하고 각 선택지에 대한 기준을 설정한다.
② 선택 기준 정의
: 각 단계에서 어떤 선택(최선의 선택)을 할지 결정하는 기준을 정의한다.
③ Greedy 알고리즘 구현
: 선택 기준을 바탕으로 각 단계에서 최적의 선택을 하는 코드를 작성한다. 보통 반복문을 사용하며, 각 단계에서의 (최선의)선택은 전체의 최적해로 이어지도록 한다.
2. Greedy 활용하기
1) 조이스틱 움직이기
2) Solution I.
① 문제 정의
즉, A..A 로부터 시작해 DFWJA와같은 입력 문자열을 만들기 위해 조이스틱을 움직이는 "최소 횟수"를 구해야한다.
② 선택 기준 정의
매 단계별 선택해야할 것은 두가지 이다.
-
현재 위치에서의 문자를 어떻게 바꿀지(다음 or 이전)
-
다음으로 이동한 위치를 어떻게 찾을지(왼쪽 or 오른쪽)
문자를 바꾸는 기준은 비교적 간단하다. 알파벳 26자를 기준으로 13번쨰를 초과하는 알파벳은 A->Z->Y->... 방식으로 찾는 것이 빠르며, 반대의 경우 A->B->C->... 방식으로 찾는 것이 최선의 선택이다.
while (found < cnt) { char c = n2[i]; // 1. 다음 or 이전 if (c - 'A' >= 13) answer += (26 - c + 'A'); else answer += (c - 'A'); ,,, }반면에, 다음의 위치를 선택하는 기준은 다소 까다롭다. 간단하게 떠올리자면 현재 위치부터 가장 가까운 'A'가 아닌 위치를 다음위치로 설정하는 것이다.
JAAAZW
i. 현재 'J' (idx=0)에 위치
ii. 'Z'의 경우 : 오른쪽으로 4번
III. 'W'의 경우 : 왼쪽으로 1번
=> 'W'위치로 이동하는 것이 최선의 선택위와 같은 선택 기준을 알고리즘으로 구현하자면?
ⓐ name 문자열을 2개 이어 붙인 n2 문자열을 선언
string n2 = name + name;ⓑ 좌우 방향 거리 탐색
// 오른쪽 for (;j < n2.length();j++) { // A가 아닌 문자 중 if (n2[j] != 'A') { // 이미 변환한 문자가 아니라면 if (j < name.length()) if (find[j] == false) { right = true; break; } else ; else if (find[j - name.length()] == false) { right = true; break; } } } // 왼쪽 for (;k >= 0;k--) { // A가 아닌 문자 중 if (n2[k] != 'A') { // 이미 변환한 문자가 아니라면 if (k < name.length()) if (find[k] == false) { left = true; break; } else ; else if (find[k - name.length()] == false) { left = true; break; } } } if (left == false || right == false) break; // a: 오른쪽으로 이동하게 될 거리 // b: 왼쪽으로 이동하게 될 거리 int a = j - i; int b = i - k;ⓒ 거리 비교 후 다음 단계
// 오른쪽 if (a < b) { i = j; answer += a; } // 왼쪽 else { i = k; answer += b; } // 다음 위치로 설정되었으므로 find(true)로 변경 if (i >= name.length()) find[i - name.length()] = true; else find[i] = true;위 코드대로 실행 시 정확도 81.5%가 나온다. seg fault가 아닌 오답으로 체킹되므로, 무언가 구멍이 있다는 것이다.
3. Solution II.
가능한 오류를 고민해보니 다음과 같다.
- 시작 위치가 문자열의 제일 처음이 아닐 수도 있다.
- 좌우 이동을 결정할 때, 현재의 최선의 선택(더 가까운 위치)이 전체 문제의 최적해가 아닌 경우가 있다.
만일, 2번의 이유라면 이 문제는 Greedy가 아닌 완전탐색을 활용할 수 있다.
1) 반례 확인
Solution I.로 해결되지 않는 반례
BBBBAAAABA
ⓐ Solution I.
![]()
ⓑ 최적의 해
![]()
그렇다면 위와 같은 반례의 경우 Solution I.의 단계별 최선의 선택이 최적의 해라는 것을 위배한다.
2) 다른 풀이
- 반례가 발생하는 이유?
현재 시점에서 최선의 선택(최소 이동거리인 위치)를 찾다보면 -> <- -> 이런식으로 방향을 여러 번 바꾸게 되는 경우가 있다. 그런데 전체 문제에서 최적의 해는 단방향 혹은 양방향(-> 한번, <- 한번)인 경우이다. 즉, 왔다 갔다 왔다를 하였을 때 전체 문제의 최적의 해가 될 수 없다는 것이다.
따라서 Greedy 알고리즘을 사용하되,방향 전환을 2번이상 하는 경우를 제외하도록 case를 다르게 분류하도록 한다.
CASE ① 단방향 이동
CASE ② 양방향 이동
CASE ②의 경우 아래와 같이 2가지 경우가 가능하다.
- 정방향->역방향(좌측) or 역방향->정방향(우측)
따라서, i+(n-j)+min(i,n-j)가 i와j에 대해 최소 이동 횟수이다. i와 j를 for문을 통해 변경해가면서 최적의 해를 탐색하도록 한다.
위 반례를 해결하기 위한 다른 풀이이다.
#include <string>
#include <vector>
using namespace std;
// 1. 상하 이동
// 알파벳별 최소 이동 횟수 : A~N -> 아래로, O~Z -> 위로
int alpha_to_move[26] = { 0,1,2,3,4,5,6,7,8,9,10,11,12,13,12,11,10,9,8,7,6,5,4,3,2,1 };
int solution(string name)
{
int answer = 0;
int n = name.length();
// CASE ① 한 방향으로 조이스틱을 이동
int min_move = n - 1;
// BBBBAAAABA
for (int i = 0;i < n;i++)
{
// 1. 상하 이동
answer += alpha_to_move[name[i] - 'A'];
// CASE ② 양방향 이동
// 1) ~i까지 정방향 탐색 후 역방향으로 j를 탐색하거나,
// 2) 원점기준으로 역방향으로 ~j까지 탐색한 후 정방향으로 i를 탐색
int j = i + 1;
while (j < n && name[j] == 'A')
j++;
// i + (n-j) = i까지 탐색 거리 + j까지 탐색 거리
// min(i,n-j) : 정방향=>역방향 or 역방향=>정방향
min_move = min(min_move, i + n - j + min(i, n - j));
}
answer += min_move;
return answer;
}
int main()
{
solution("BBBBAAAABA");
return 0;
}위 코드를 보다보면, 결국 단계별 최선의 선택이 아닌 문제 전체의 최적의 해(min을 사용하므로)을 구하는 방식이라 greedy만으로는 온전한 풀이를 만들 수 없는 것처럼 보인다.
이 문제의 경우 2022년도에 테스트케이스가 추가된 이후로 위와 같이 케이스 분류하지 않는 경우 통과할 수 없는 문제가 된 것 같다. 실제로 2022년도 이전에 구글링하여 찾은 답을 돌려보면 통과하지 않는다.
2024.10.05 재풀이해본 소스
※ 기존 source
#include <string>
#include <vector>
using namespace std;
// 1. 상하 이동
// 알파벳별 최소 이동 횟수 : A~N -> 아래로, O~Z -> 위로
int alpha_to_move[26] = { 0,1,2,3,4,5,6,7,8,9,10,11,12,13,12,11,10,9,8,7,6,5,4,3,2,1 };
int solution(string name)
{
int answer = 0;
int n = name.length();
int min_move = n - 1;
for (int i = 0;i < n;i++)
{
answer += alpha_to_move[name[i] - 'A'];
// 2. 좌우 이동
int j = i + 1;
while (j < n && name[j] == 'A')
j++;
min_move = min(min_move, i + n - j + min(i, n - j));
}
answer += min_move;
return answer;
}※ 신규 소스 (오답 소스)
#include <string>
#include <vector>
#include <iostream>
using namespace std;
// 알파벳 갯수 : abcdefghijklm / n(13-동일) / o(12)pqrstuvwxyz(1)
// j (9)
// a (1+0)
// n (1+13)
int solution(string name)
{
int answer = 0;
int len = name.length();
int mid = (len/2 +1);
// aaa...aa 로 시작
for(int i=0;i<len;i++)
{
if(name[i]=='A') continue;
// 좌우 움직임
if(i>=mid) // 끝으로 돌아가서 움직임
answer+=(len-i);
else
answer+=1;
// 상하 움직임
if(name[i]<='N')
answer+=(name[i]-'A');
else
answer+=('Z'-name[i]+1);
}
return answer;
}위 경우는 정방향(->) 후 역방향(<-)으로 움직이는 경우가 최적의 해라고 가정하고 있다. 그러나 단방향(->)이 최선일 수도 or 역방향(<-) 후 정방향(->)이 최적의 해가 될 수도있 경우를 포함하지 않는다.