[알고리즘] DFS/BFS 활용 ⑤

1. 개요

프로그래머스 PCCP 기출/석유시추 lv2.

1) 문제 개요

NxM 격자 지도 위 석유가 존재한다. 석유는 "덩어리" 단위로 존재하며, 시추관은 "수직으로" 단 하나만 뚫을 수 잇다. 이때 가장 많은 석유를 뽑을 수 있는 시추관의 위치를 찾도록 한다.

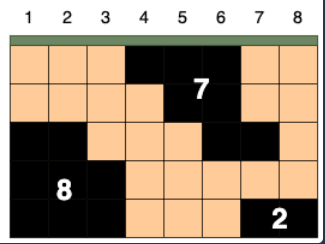
만약 위와 같이 석유가 존재하는 경우

• 1~3 열 사이에 시추를 한다면
  -> 시추한 석유양 : 8
• 7열에 시추를 한다면
  -> 시추한 석유양 : 9

따라서 시추관의 위치에 따라 최대 획득 가능한 석유양은 9이다.

2) 입출력 예시

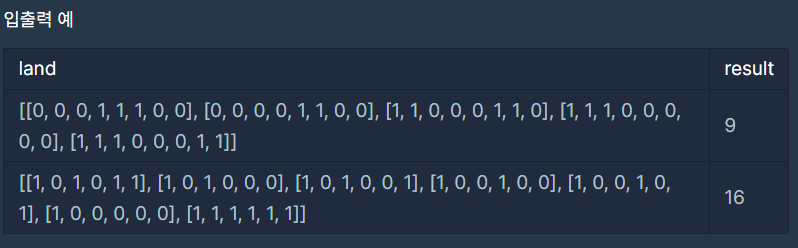
3) 제한사항

2. Solution I.

1) 알고리즘 개요

① DFS 를 통해 석유 덩어리를 파악

② 석유 덩어리의 순번과 사이즈를 map 형태로 저장

③ 각 열을 1~n행까지 검사하여, 포함된 석유 덩어리를 파악

④ 각 열에 포함된 석유 덩어리를 토대로 각 열의 <석유 덩어리 수확량의 합>을 계산

⑤ 최대의 석유 수확량을 반환

#include <string>
#include <vector>
#include <iostream>
#include <map>
using namespace std;
int n,m;
int cnt=1;
int oilSize=1;
int dx[4]={0,0,1,-1};
int dy[4]={1,-1,0,0};
vector<vector<int>> mp;
vector<vector<bool>> v;
map<int,int> oilInfo;

void dfs(int x,int y)
{
    for(int k=0;k<4;k++)
    {
        int nx=x+dx[k];
        int ny=y+dy[k];
        if(nx<0||ny<0||nx>=n||ny>=m) continue;
        if(mp[nx][ny]==1 && v[nx][ny]==false)
        {
            v[nx][ny]=true;
            mp[nx][ny]=cnt;
            oilSize++;
            dfs(nx,ny);
        }    
    }
}

int solution(vector<vector<int>> land) 
{
    int answer = 0;
    n=land.size();
    m=land[0].size();
    mp=land;
    v = vector<vector<bool>>(n,vector<bool>(m,false));
    for(int i=0;i<n;i++)
    {
        for(int j=0;j<m;j++)
        {
            if(mp[i][j]==1 && v[i][j]==false)
            {
                v[i][j]=true;
                // size 값 초기화
                oilSize=1;
                mp[i][j]=cnt;
                dfs(i,j);
                oilInfo[cnt] = oilSize;
                // 석유 덩어리 순번 증가
                cnt++;
            }
        }
    }
    // 2. 열별 시추 대상 확인
    for(int j=0;j<m;j++)
    {
        int sum=0;
        map<int,int> oil;
        for(int i=0;i<n;i++)
            if(mp[i][j]!=0)
                oil[mp[i][j]]++;
        
        // 2-2. 석유량 합계 계산
        for(auto iter = oil.begin();iter!=oil.end();iter++)
            sum+=(oilInfo[iter->first]);

        if(sum>answer) answer = sum;
    }
    
    // 3. 최대값 반환
    return answer;
}