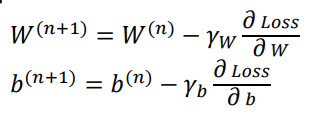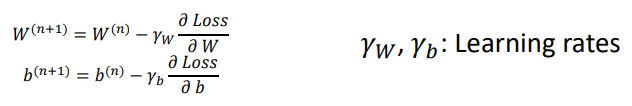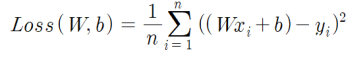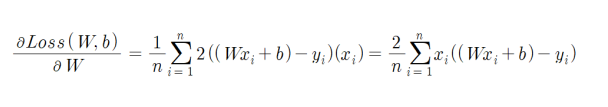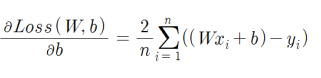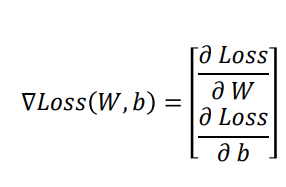Linear Regression Model을 활용해 Loss Function이 최소가 되는 W,b를 사용한 F(x)=Wx + b,즉 선형 함수를 학습시키는 모델이다. 그러나 W와 b를 구하기 위해 loss function을 미분하거나 완전제곱식으로 바꾸는 연산이 필요하다. 하지만, 이는 매우 단순한 모델에만 적용되는 현실성이 떨어지는 방식이다. 이를 극복하고 F(x)구하는 과정을 최적화하고자 Gradient Descent 방법을 사용해볼 수 있다.
1. Gradient Descent (경사하강법)
Gradient Descent(경사 하강법)는 기계 학습과 최적화 분야에서 사용되는 반복적인 최적화 알고리즘입니다. 이 알고리즘은 모델의 손실 함수(비용 함수)를 최소화하기 위해 모델의 매개 변수를 조정하는 데 사용됩니다. Gradient Descent는 주로 다양한 기계 학습 모델의 훈련에 적용되며, 이를 통해 모델이 데이터에 가장 적합한 매개 변수 값을 찾을 수 있습니다.
1) 주요 아이디어
1) 초기 매개 변수 값에서 시작
2) 손실 함수의 그래디언트(기울기)를 계산 ( 이 그래디언트는 현재 매개 변수 값에서의 손실 함수의 기울기)
3) 그래디언트의 반대 방향으로 매개 변수를 조금씩 조정
-> 이를 통해 손실을 최소화하려는 방향으로 이동
4) 일정한 학습률(learning rate)을 사용하여 각 반복에서 얼마나 크게 이동할지를 결정
- 이 과정을 여러 번 반복하면 손실 함수가 최소값에 수렴하게 되고, 모델의 매개 변수는 최적화됩니다. Gradient Descent는 주로 최적화 문제를 푸는 데 사용되며, 기계 학습 모델의 훈련 중에 사용되는 일반적인 최적화 알고리즘입니다.
2) Update Rule for GD
W(n+1), b(n+1) 을 갱신하기 위해 loss function의 미분값과 "반대 방향"으로 가중치를 더해줌으로써 점차 최소값에 수렴하도록 한다.
3) Learning Rate
- Learning rate is too slow
-> 최솟값에 도달하기 위해 너무 오랜 시간이 소요 - Learning rate is too high
-> 최솟값에 도달하는 과정에서 "발산"할 수 있음
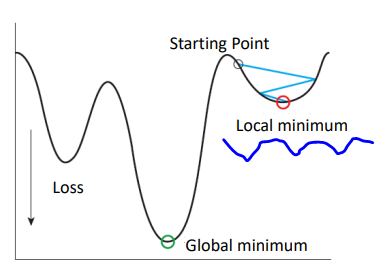
4) Problem for GD : Local Minima Problem
위와 같은 Gradient Descent 방식의 문제점은 부분 최솟값 이슈가 존재한다.
우리가 찾고자 하는 함수 전체의 최솟값을 만드는 W와 b인데, 위와 같은 모델은 시작점에 따라 부분 최솟값을 찾아낼 수 있다.
2. SGD(Extension to Higher Dimension)
1) GD Function
GD의 경우 다음과 같이 summation을 활용해 loss function을 구성한다.
① avg of loss with (w,b) is avg of summation of square of (y-f(x))
② training w
③ training b
-> 메모리를 많이 차지하며, 연산 성능에 영향을 많이 받는다.
2) GD Extension to higher dimenstion
Loss(W,b)에 대해 "그레디언트"는 다음과 같이 계산된다.
즉 Loss function의 W 미분값과 b 미분값을 모아 구성된 값이 그레디언트 값이다.
"gradient"란, "loss function"을 최소화하기 위해 모델 매개변수(예를 들면 w와 b 등)를 조정할 때, 현재 매개변수 값에서의 미분(기울기) 정보를 나타낸다. 이 미분 정보는 어떤 방향으로 매개변수를 업데이트해야 "loss function"을 줄일 수 있는지를 알려줍니다.
3) SGD
그렇다면 이 summation을 분할해서 batch단위로 수행한다면?
- Stochastic Gradient Descent는 매번 학습 데이터 중 하나의 데이터 포인트 또는 미니 배치(작은 데이터 그룹)에 대한 손실 함수의 그래디언트를 계산하여 모델의 매개 변수를 업데이트
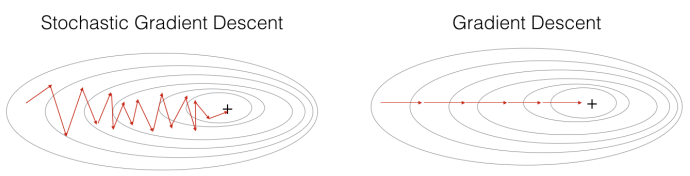
-> 이것은 전체 데이터 세트 대신 데이터의 랜덤한 부분을 사용하므로 계산이 빠르고, 더 빠른 수렴dl 가능
-> but, 확률적성(랜덤성)을 가지기 때문에 수렴이 덜 안정적이며, 수렴하는 동안 손실 함수가 흔들릴 수 있음
★ SGD is faster but "oscillates" more
Comparition of GD and SGD
linear model : f(x) = wx + b
① GD
② SGD
3) Application
이와 같은 SGD는 데이터가 대량으로 존재하는 경우, 분산된 경우 사용된다.