
Hash Table
해쉬 테이블이란 item search를 빠르게 할 수 있다는 장점을 갖는 collection of item이다. 이러한 Hash Table의 각 position을 slot이라고 하며, 이 slot에 item을 담을 수 있게 된다. 이러한 Hash Table은 평균적인 검색 복잡도는 O(1)이 된다.
Python에서는 dictionary가 이 Hash Table이기에 사실 새롭게 구현을 할 필요는 없으나 그 개념을 파악하고 간다는 생각으로 읽으면 좋을 것 같다.
Hash function
Hash function은 item을 Hash Table의 slot에 mapping 시켜주기 위한 함수이다. 작동방식은 넣고 싶은 item을 받아, 0~m-1(table 크기가 m일때)사이의 slot name을 return 해주고, 이 slot에 해당 item을 집어 넣게 된다.
다음은 여러 종류의 Hash function이다.
-
remainder method
input 값을 Table 크기로 나눈 나머지를 주소값으로 사용한다.

-
folding method
input값을 동일한 size로 쪼갠후 더해서 remainder method를 사용한다.
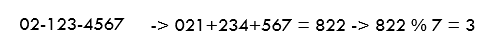 위와 같이 size가 7인 Hash Table에 넣는다는 가정하에서 '02-123-4567'은 slot 3에 들어갈 것이다.
위와 같이 size가 7인 Hash Table에 넣는다는 가정하에서 '02-123-4567'은 slot 3에 들어갈 것이다. -
mid-square method
input 값을 제곱하여 나온 숫자의 중간에서 input 값 길이만큼의 숫자를 빼내고, 그 숫자에 remainder method를 적용시키는 방법이다.
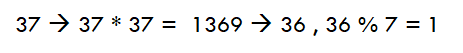 위와 같이 size가 7인 Hash Table에 넣는다는 가정하에서 '37'은 slot 1에 들어갈 것이다.
위와 같이 size가 7인 Hash Table에 넣는다는 가정하에서 '37'은 slot 1에 들어갈 것이다. -
Non-integer elements
숫자가 아닌 문자의 경우 ord()를 이용해 unicode로 변환 시켜 더한 후 remainder method를 이용하기도 한다.
collision Resolution
Hash Table에 item을 넣다보면 hash function의 output 값이 같아 동일한 slot에 다수의 item이 들어가야 하는 경우가 있다. 이런 상황을 collision이라고 하며 아래는 이를 해결하기 위한 방법이다.
- open addressing
open addressing의 핵심은 결국 hash table의 각 칸에는 한가지 값만 넣는 다는 것이다. 이 open addressing에도 여러 방식이 있는데, 이 글에서는 세세하게 설명하지 않는다. 이 링크에서 더 자세한 설명을 확인할 수 있으니 읽어볼 것을 추천한다. - chaining
chaining은 동일한 slot에 다수의 item이 들어오면, 해당 slot에 linked list와 같은 방식으로 다수의 item을 담을 수 있도록 하는 것이다.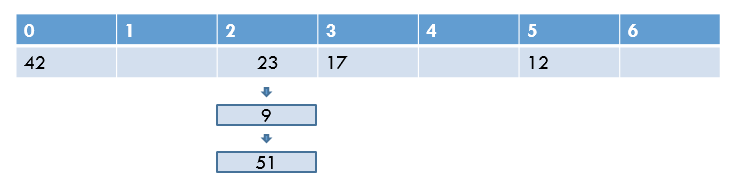 이를 통해 slot과 item간의 관계를 해치지 않고 데이터를 저장할 수 있다.
이를 통해 slot과 item간의 관계를 해치지 않고 데이터를 저장할 수 있다.
구현
앞서 말했든 이미 python에서는 dictionary로 잘 구현되어 있지만, 실제로 list를 이용하여 직접 구현해보면 그 logic이 더 잘 이해될 것이다. 코드는 다음과 같으며, 설명은 중간에 주석으로 달아두었다.
class Node: #SLList를 이용하기 위해 작성한다.
def __init__(self, val):
self.val = val
self.next = None
class HashTable:
def __init__(self, size):
self.size = size
# slot은 key table이고, data는 data table이라고 생각하면 된다.
self.slots = [None] * self.size
self.data = [None] * self.size
# hashfunction으로는 remainder method를 이용한다.
def hashfunction(self, key, size):
if type(key) == int:
return key % size
else:
return sum(ord(s) for s in key) % size
def put(self, key, data):
# hashfunction을 통해 key 변환
hashvalue = self.hashfunction(key, self.size)
# 해당 hashvalue가 비어있으면 key와 data를 모두 넣는다.
if self.slots[hashvalue] == None:
self.slots[hashvalue] = Node(key)
self.data[hashvalue] = Node(data)
# 비어있지 않으면 iteration을 통해 해당 key값이 있는지 없는지 확인한다.
else:
cur_slot = self.slots[hashvalue]
cur_data = self.data[hashvalue]
while True:
# 있다면 새로 들어온 data로 기존의 data를 대체해준다.
if cur_slot.val == key:
cur_data.val = data
# 없다면 SLL의 마지막에 새로운 Node를 추가해준다.
# 이 부분은 사실 어색하긴 하다. SLL의 경우 append가 되면 맨 앞(head)
# 부분에 새롭게 추가되는게 맞기는 하나, 이 case에서는 마지막까지 항싱
# search 하므로 그냥 마지막에 생성해주었다.
# 구현상 더 나은 방법이 있을 것 같기는 하다.
else:
if cur_slot.next is None:
cur_slot.next = Node(key)
cur_data.next = Node(data)
break
else:
cur_slot = cur_slot.next
cur_data = cur_data.next
def get(self, key):
target = self.hashfunction(key, self.size)
cur_slot = self.slots[target]
cur_data = self.data[target]
# put과 비슷한 맥락으로 iteration을 통해 값을 searching 한다.
while True:
if cur_slot.val == key:
return cur_data.val
else:
if cur_slot.next is None:
return None
else:
cur_slot = cur_slot.next
cur_data = cur_data.next
# python method를 통해 [] 활용이 가능하도록 만든다.
def __getitem__(self, key):
return self.get(key)
def __setitem__(self, key, data):
self.put(key, data) Performance
이런 Hash Table은 size가 정해져 있기 때문에 performance에 영향을 주는 추가적인 요소는 바로 Linked List의 길이가 될 것이다. Table의 size가 m이고 max(length of Linked List)가 k라고 할 때 in method는 O(k) <= O(n) 이 들 것이다.
Problem
N개의 item을 m size의 Hash Table에 넣는다고 생각하면 k는 N/M(고르게 분포되어 있을 때)과 N(한 곳에 몰려 있을때) 사이의 값이다. 이 두가지 모두 결국 N이 들어있기에 in operation의 time complexity가 O(N)이 될 것이다.
Solution
이러한 문제를 해결하여 원래 얻으려 했던 O(1)의 in operation을 만드려면 Resizing을 해야 한다. 그 방식은 N이 커짐에 따라 M도 키워서 결국 O(N/M) => O(1)이 되게 하는 것이다.
예시 ) N/M >= 1.5가 되면 M을 2배 해준다.
만약 M=5일때, item수 N이 0부터 1씩 늘어나다보면 N=8이 되는순간 처음으로 N/M이 1.5를 넘어서게 된다. 이 경우 M=10으로 늘려주고(두 배 해주는 것이다) hashfunction을 다시 적용시켜 Redistributing 해주는 것이다. 이런 식으로 N/M사이의 관계를 유지시켜 나가 M을 N의 상수배로 유지키셔 결국 O(1)을 만들어 내는 것이다.
다만 이 경우는 resizing의 cost를 제외한 것이다. N개의 item에 대해서 Resizing을 하는 것은 O(N) time이 걸리게 된다. 그러나 이 문제는 resizing size에 의해 해결된다. 위에서 M을 2배씩 늘려나갔기 때문에 총 N개의 item을 저장하는데 있어 resizing time은 아래와 같이 걸릴 것이다.
- 1+2+4+8+ ... +N = 약 2N-1
이 뜻은 N개의 item을 더하는 동안 2N-1 time이 걸린 것이다. 즉 평균을 구해본다면 O((2N-1)/N) = O(1)이 되기 때문에 결국 resizing time도 평균적으로 O(1) 상수가 되어 결국 총 time complexity도 O(1) 상수화 시킬 수 있는 것이다!
마치며
여러 자료들을 찾아보다 보니 위에 설명한 flow 말고 table의 sizing 개념을 일전에 잡아두지 않고 Hash function을 통해 value를 구한 후, 그 value의 reduction과정을 추가하여, 이 과정에서 size를 제한하는 경우도 봤다. 이 때는 Hash function에서는 input을 소수 진수화 하여 최대한 collision을 줄이도록 하는 경우도 있었다. 다만 결국 Hash를 사용하는 목적은 동일하므로 그런 방식도 있구나, 정도 생각하고 넘어가면 좋을 것 같다.
