백준 2292_벌집.cpp

소스코드

#include <iostream>
using namespace std;
int main(){
    int num;
    cin >> num;
    if(num == 1){
        cout << 1 << endl;
        return 0;
    }
    int cnt = 0;
    int block = 0;
    while(cnt < num){
        block++;
        cnt = 1 + ((6+6*block)*block)/2;
    }
    cout << block+1 << endl;
    return 0;
}

//velog 코딩리뷰 하면서 반복문 다시 한번 확인하기
// 등차수열, 바퀴수만 고려하면됨

1. 변수
   int num : 입력받은 수
   int block : 징검다리 개수(몇 겹을 넘어갔는지)
   int cnt : 해당 겹까지의 총 벌집 개수

2. 알고리즘
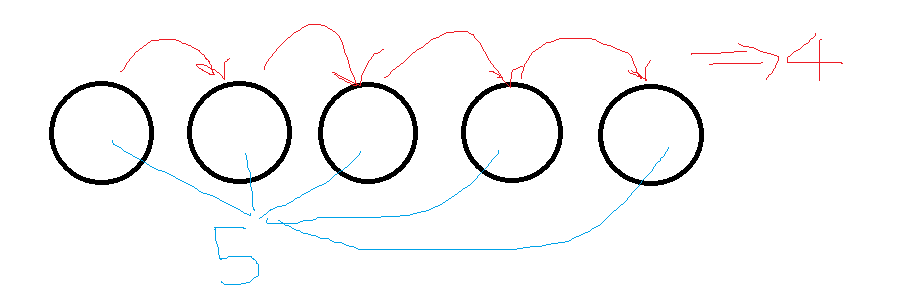
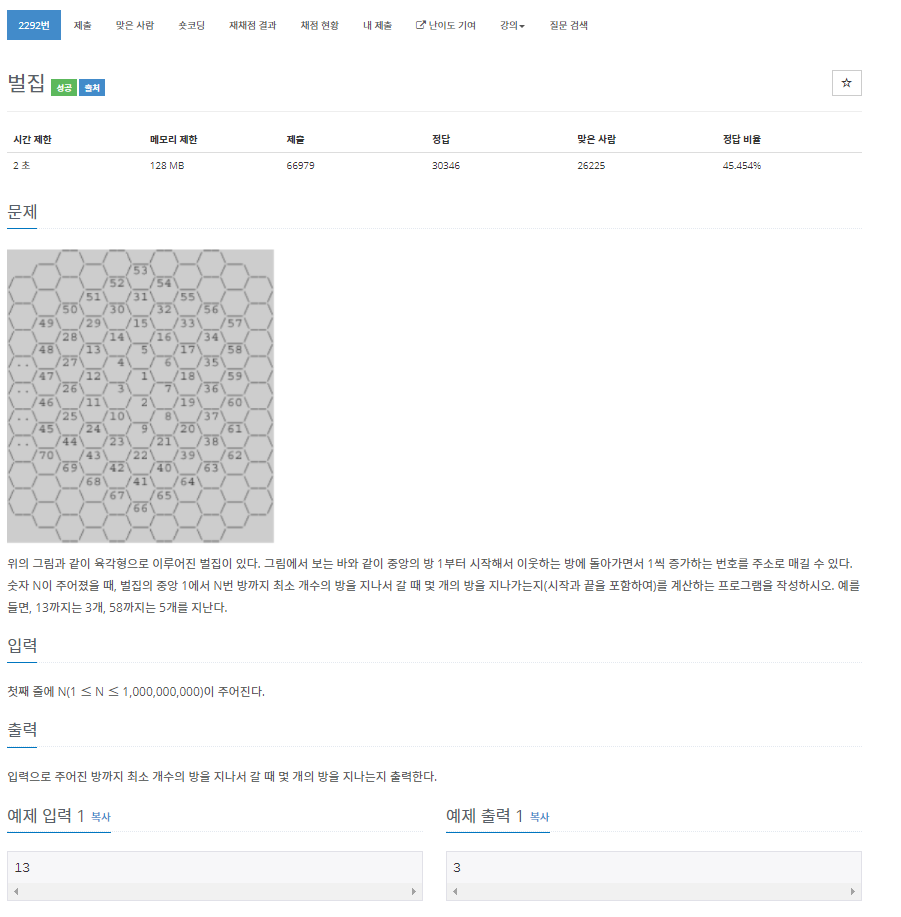
   방의 갯수를 잘보면
   1개 - [1]
   6개 - [2~7]
   12개 - [8~19]
   18개 - [20~37]
   24개 - [38~61]
   6 * 겹겹이 수
   겹겹이 쌓이는 숫자와 1 에서 접근할 수 있는 개수의 최소값이 "같음"을 알 수 있습니다.
   1 = 1칸
   2~7 = 2칸
   8~19 = 3칸
   20~37 = 4칸
   많이 고민했는데 어느 순간 어? 하고 규칙을 발견하게 된 문제이다 ㅋㅋㅋㅋㅋ 위에 내용은 내가 생각했던? 내용을 더 잘 설명해둔 내용을 퍼온것이다.
   1) 기본적인 알고리즘은 위에 내용을 토대로 했다.
   2) 등차수열의 합 공식을 활용해서 해당 겹까지의 총 벌집 개수(cnt)를 구했다. 여기서 +1을 한 이유는 첫번째 1은 등차수열에 포함되지 않기 때문에 따로 더해주어야 하기 때문이다.
   3) cnt가 입력한 벌집(num)보다 커질때까지 다음 겹(block++) 반복문을 통해서 만들었다.
   4) 마지막 block+1을 한 이유는 애초에 다음 겹으로 몇 번 넘어갔는지를 구한 코드기 때문에 block+1을 출력한다.
   

3. 배운점

4. 아쉬운점&느낀점
   1) 코딩리뷰가 뭔가 깔끔하게 되지 않는다는건, 내가 확실히 제대로 풀었는지도 의심해봐야 되는 거 같다. 확실히 푸는 연습 그것을 정확히 리뷰하는 것을 연습해야겠다.(사실 제일 귀찮긴 하다.)
   2) 수학 알고리즘 문제는 규칙을 찾는 것이 우선이라는 것을 다시 한번 느낀 문제었다.