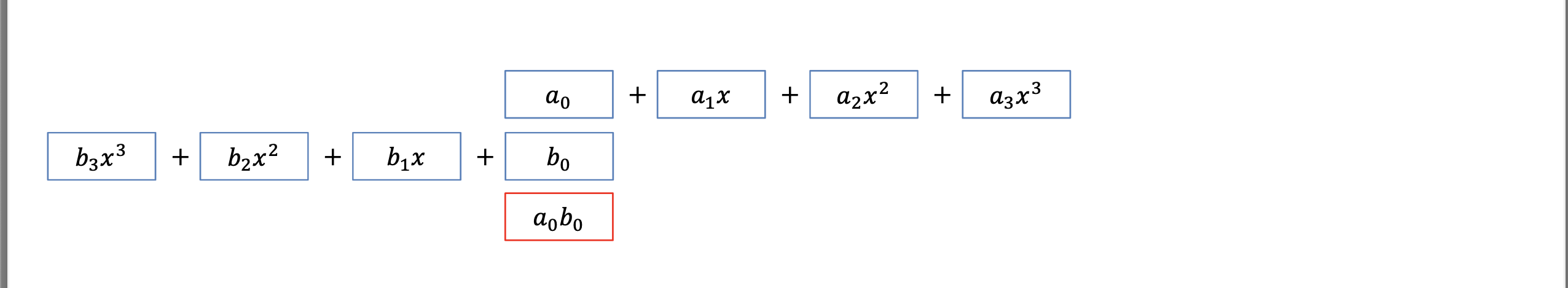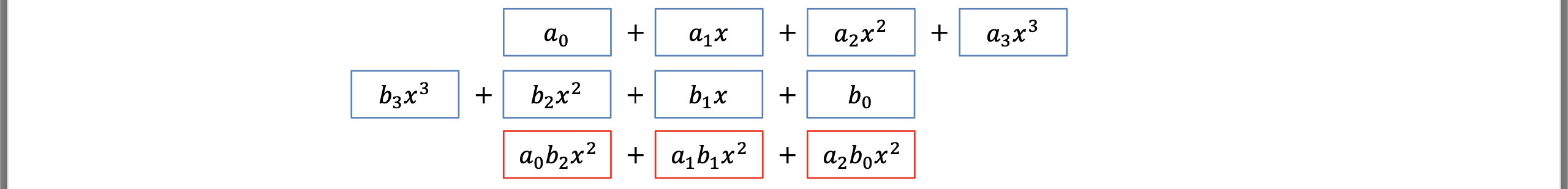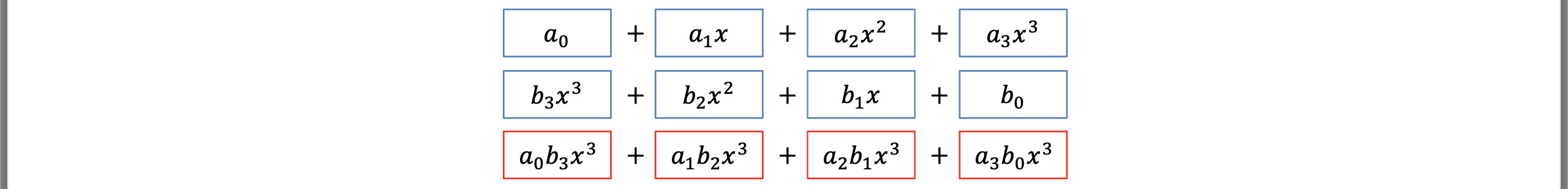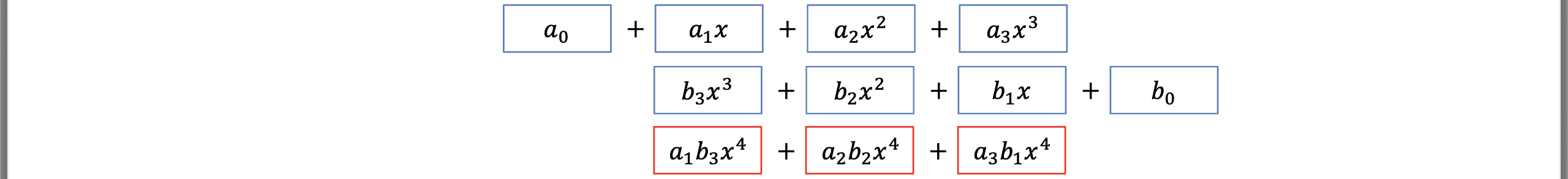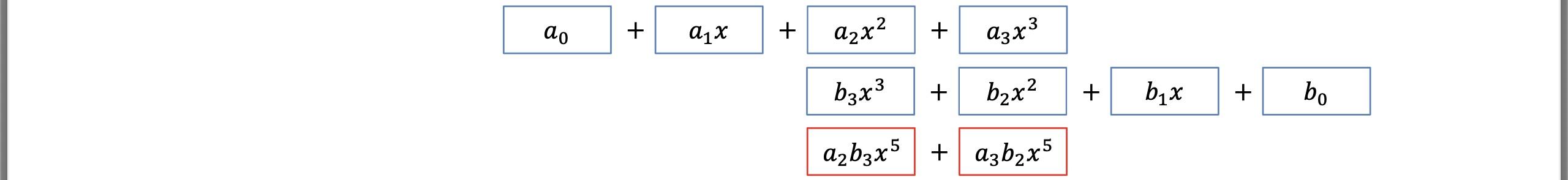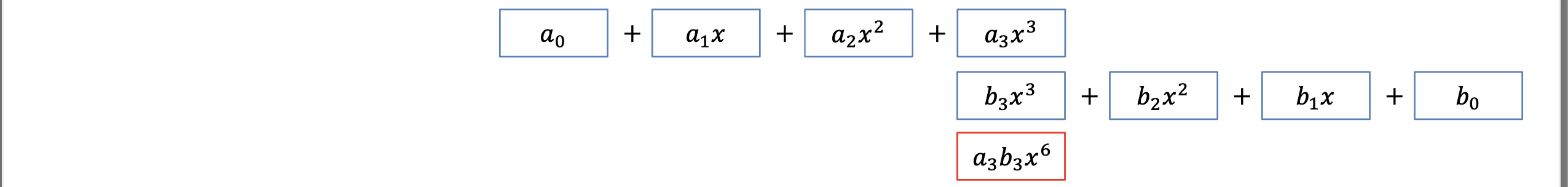[Algorithm] FFT

HDuckkk·2023년 9월 12일

FFT algorithm

Algorithm

목록 보기

3/3

FFT

이번에 학교에서 연구를 진행하면서 FFT를 공부하게 되었다. 이는 나의 공부과정을 정리한 내용이며 틀린 내용이 있을 수 있으니 만일 보시는 분들이 있다면 참고바란다.
~~부끄러우니 다른거 보세요~~

GOAL : Fast Multiplication in polynomial

다항식의 곱은 Convolution으로 해결할 수 있다.

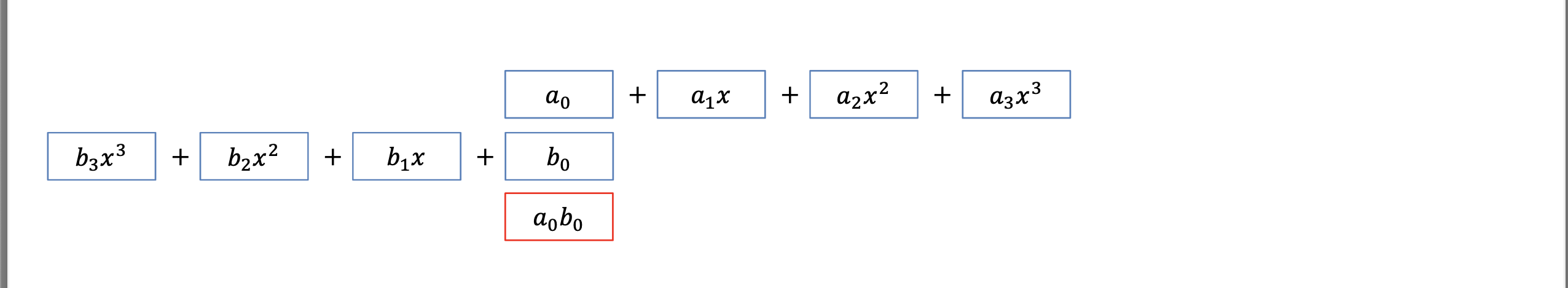
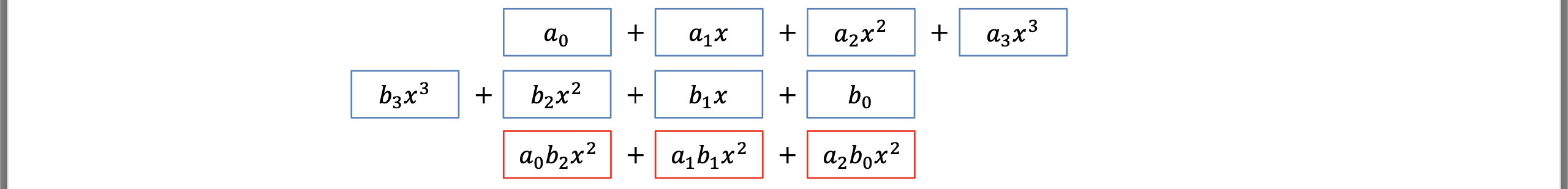
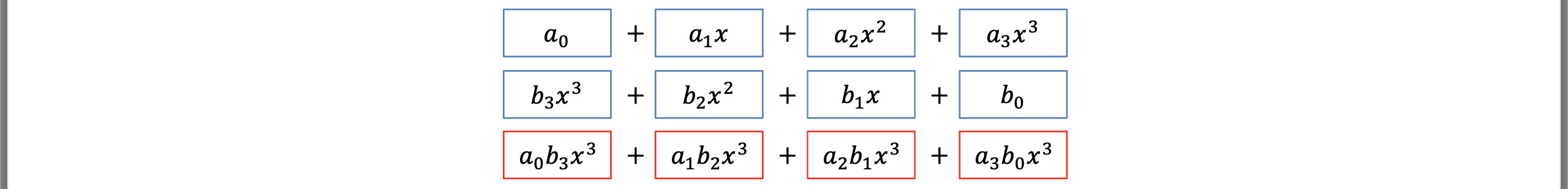
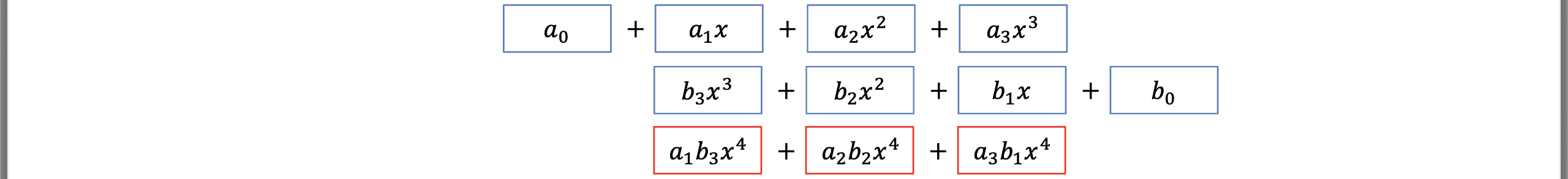
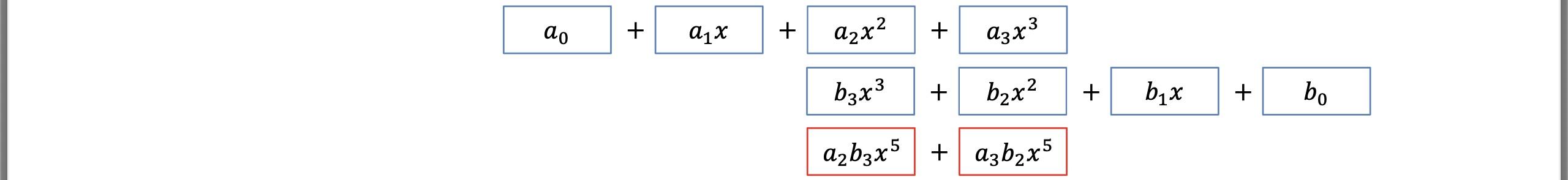
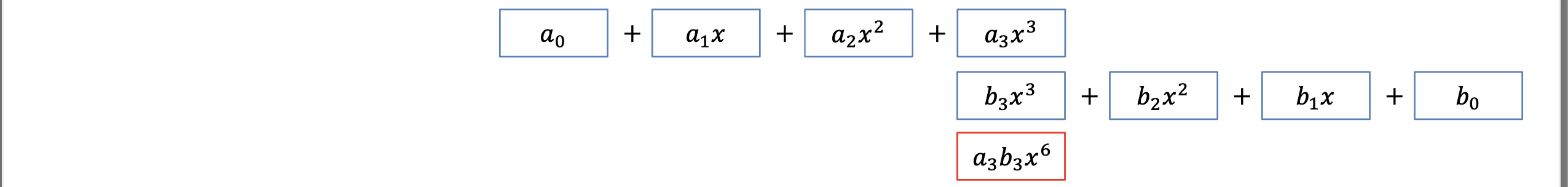
위의 과정은 단간하게 표현한 Convolution의 과정이다.

일반적인 Convolution은 $O(N^2)$ 의 시간복잡도를 갖는다. 그러나 FFT를 활용한다면 보다 효율적으로 계산을 수행할 수 있다.

Representation of polynomial

우선 다항식을 표현하는 두가지 방법이 있다는 것을 알아두자.

Coefficient representation

A(x) = \sum^{N-1}_{j=0} a_j x^j \\ A(x) = a_0 + x(a_1 \; + \; x(a_2 \; + \cdots +x(a_{N-2} \; + x(a_{N-1})))) \\ A(x) = a_{N-1}x^{N-1} + \cdots + a_1x^1 + a_0

Point-value representation

{ (x_0, A(x_0)), \; (x_1,A(x_1)), \; (x_2, A(x_2)), \; \cdots (x_{N-1},A(x_{N-1})) }

즉, 서로다른 $x$ 에 대해 고유의 값 $A(x)$ 를 N개의 집합 표현하는 것이다.
행렬로 표현한다면 다음과 같다.

\begin{bmatrix} A(x_0) \\ A(x_1) \\ A(x_2) \\ \vdots \\ A(x_{N-1}) \end{bmatrix} = \begin{bmatrix} x_0^0 & x_0^1 & x_0^2 & \cdots & x_0^{N-1} \\ x_1^0 & x_1^1 & x_1^2 & \cdots & x_1^{N-1} \\ x_2^0 & x_2^1 & x_2^2 & \cdots & x_2^{N-1} \\ \vdots & \vdots & \vdots & \cdots & \vdots \\ x_{N-1}^0 & x_{N-1}^1 & x_{N-1}^2 & \cdots & x_{N-1}^{N-1} \end{bmatrix} \begin{bmatrix} a_0 \\ a_1 \\ a_2 \\ \vdots \\ a_{N-1} \end{bmatrix}

~~벌써부터 머리가 아프다. 🥲~~

Why?

왜 이런식으로 표현할까? 혹은, 이런식으로 표현하는 것이 허용될까?

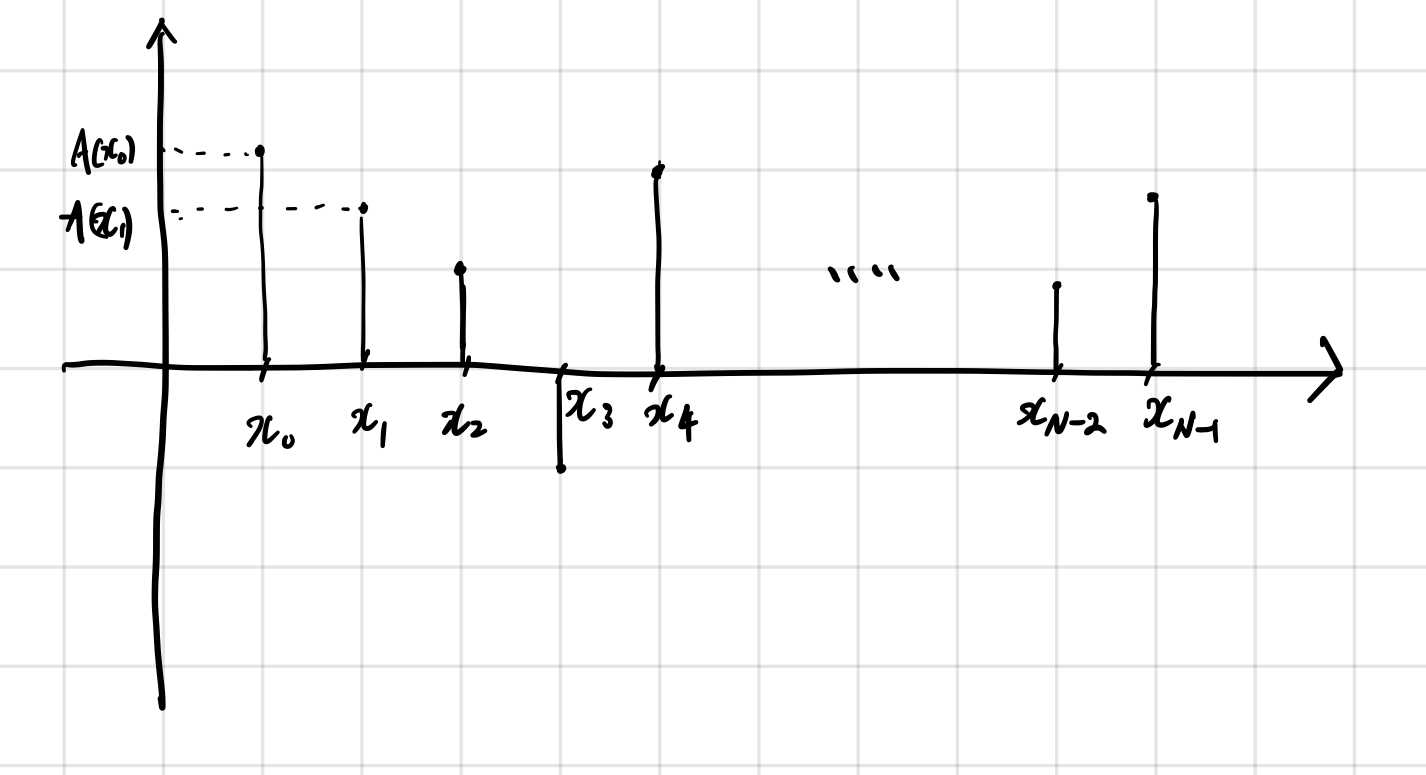
다음과 같은 순서쌍의 집합이 있다고 가정해 보자. 모든 점을 지나는 다항식은 몇개나 존재할까? 답은 무수히 많을 것이다. 그러나 놀랍게도 모든 점을 지날 수 있는 다항식의 최소 차수는 $N-1$ 차 이며 무려 유일하다.

그렇다면 다음의 식이 성립한다. 다항식 $A(x)$ 와 $B(x)$ 가 있다고 하자. 이 둘의 곱을 구하고자 하는데 만일 두 다항식이 어떠한 값 $\omega$ 에 대하여 $( \omega, A(\omega)), (\omega, B(\omega))$ 가 주어져 있다고 하면 두 다항식의 곱 $C(\omega)$ 는 $(\omega, A(\omega) \cdot B(\omega))$ 를 만족할 것이며 역시나 유일할 것이다.

도대체 이렇게 꼴을 바꾸어서 곱을 수행하는게 왜 유리할까? 조금만 생각해보자 기존에는 Convolution과 같은 알고리즘을 이용하여 $O(N^2)$ 에 수행되었지만, 이런식으로 꼴을 바꾼다면 각 $\omega$ 일 때, $A(\omega) \cdot B(\omega)$ 만을 수행하면 되므로 $O(N)$ 안에 수행되게 된다.

FFT

앞서 알아본 두가지의 표현법 간의 변환을 빨리 해주는 것에 FFT가 이용된다.

Coefficient representation to point-value representation
Point-value representation to Coefficient representation

Coefficient representation to point-value representation

일반적인 경우 N개의 $A(x_i)$ 를 구하기 위해 N개의 $\sum^{N-1}_{j=0} x_i^ja_j$ 를 수행하야 하기 때문에 시간복잡도는 $O(N^2)$ 이 될 것이다.

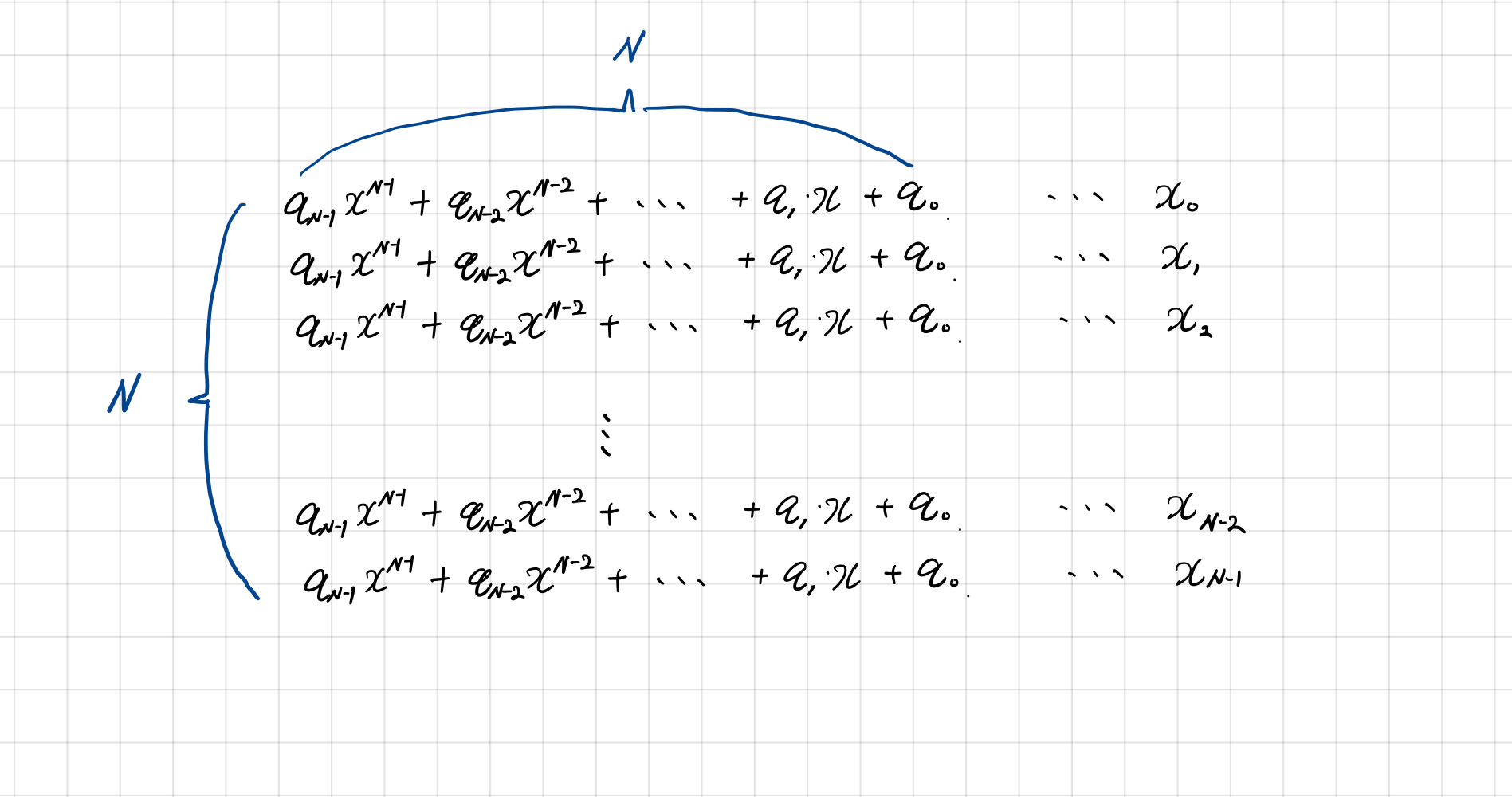
이를 빠르게 수행하는 것이 FFT 이다.

만일 다항식 $\bold{A}$ 와 $\bold{B}$ 가 있다고 가정하자. 다항식의 차수는 N-1차 다항식이며 이 둘의 곱을 $\bold{C}$ 라 하면, $\bold{C}$ 는 2N-2차 다항식이 될 것이다. 여기서 우리가 2N-1개의 대한 서로다른 $(x_i, \bold{C}(x_i))$ 가 있다면, 두 다항식의 곱을 구해낼 수 있을 것이다.

생각해보면 FFT를 이용하지 않는다고 가정하면 다항식 $\bold{A}$ 와 $\bold{B}$ 가 둘다 $N$ 차 다항식이라 가정할 때, 각각의 다항식을 변환하기 위해 $O(N^2)$ 이 소요되므로 일반적으로 보았을 때 시간복잡도는 $O(N^2 + N^2) = O(2N^2)$ 으로 별 차이 없을것이다.

$\bold{A}$ 와 $\bold{B}$ 를 각각 $(x_i, \bold{A}(x_i))$ 와 $(x_i, \bold{B}(x_i))$ 로 표현한 뒤, 이를 이용하여 $(x_i, \bold{C}(x_i))$ 를 구해낸다고 해보자.
여기서 FFT는 아래의 디테일을 이용하여 계산시간을 획기적으로 줄인다.

\bold{A}(x) = x^4 + 7x^2 + 10x^0 \\ \bold{B}(x) = 2x^5 + 3x^3 + 11x^1

위와 같이 $\bold{A}$ 는 짝수항을 갖는 다항식, $\bold{B}$ 는 홀수항을 갖는 다항식이라 해보자.
여기서 우리가 임의의 $(x_i, \bold{A}(x_i))$ 와 $(x_i, \bold{B}(x_i))$ 를 구했다고 해보자. 그렇다면 다음의 항도 쉽게 구할 수 있을 것이다.

(x_i, \bold{A}(x_i)), \;\; (-x_i, \bold{A}(x_i)) \\ (x_i, \bold{B}(x_i)), \;\; (-x_i, -\bold{B}(x_i))

이는 짝수항만을 갖는 다항식과, 홀수항만을 갖는 다항식으로 가정했기 때문에 가능한 것이며, 임의의 다항식이 주어졌을 때 각각 짝수, 홀수항만을 갖는 다항식으로 만든뒤 두 다항식을 더해주는 연산은 다항식의 최고차수에 비례하기 때문에 크게 문제되지 않을 것이다.

일반적인 경우에는 다항식을 짝수, 홀수항만을 갖는 다항식으로 나눈다면 계산이 절반으로 줄어들 것이다.

P(x) = P_{e}(x^2) + xP_o(x^2) \\ P(x_i) = P_e(x_i^2) + x_iP_o(x_I^2) \\ P(-x_i) = P_e(x_i^2) - x_iP_o(x_i^2)

이를 보다 이해하기 쉽게 표현해보자.

A(x_i) = a_0x^0_i + a_1x^1_i * \cdots +a_{N-1}x^{N-1}_i \\ = (a_0x^0_i + a_2x^2_i+\cdots+ a_{N-2}x_i^{N-2}) * x_i(a_2x^0_i + a_4x^2_i+\cdots+ a_{N-1}x_i^{N-2})

여기서 우리는

P_e(x_i^2) = (a_0x^0_i + a_2x^2_i+\cdots+ a_{N-2}x_i^{N-2}), \\ P_o(x_i^2) = (a_2x^0_i + a_4x^2_i+\cdots+ a_{N-1}x_i^{N-2 })

라 하는 것이다.

그러나 이런식으로 계산과정을 절반으로 줄였다고 하더라도 결국 큰 효과를 보지는 못한다.

$O((\frac{N}{2})^2 + (\frac{N}{2})^2) = O(\frac{N^2}{2}) = O(N^2)$ . ~~사실 의미 없다.~~

이를 빨리 수행하기 위해 등장하는 개념이 바로 FFT이다.

즉, 임의의 $x_i$ 를 $\omega_N = \cos(\frac{2\pi}{N}) + i\cdot \sin(\frac{2\pi}{N})$ 로 설정하는 것이다. 기존의 $N$ 을 절반으로밖에 줄이지 못했었지만 이렇게 설정한다면, 무려 $O(\log{N})$ 안에 수행할 수 있다.

왜 이렇게 되는지는 다음의 동영상을 참고하면 매우 도움이 된다.

세상을 바꾼 알고리즘
~~목소리가 좋으시다~~
But what is the Fourier Transform? A visual introduction.

요약 : 사인파, 코사인파의 주기성 등 다양한 특성을 이용하면 주기가 다른 파형에 대해서 규칙성을 보여 값의 재사용이 허용된다. 쉽게 말해 앞서 홀수항과, 짝수항을 나누었던 과정을 그 길이가 1이 될 때 까지 무한정 반복할 수 있다는 것이다.

이 컨셉에 대하여 잠시 알아보자. 어째서 홀수항과 짝수항을 무한히 구분할 수 있는 것인가? 정확히 표현하자면 무한히 홀수항과 짝수항을 나눌수 있는 것이 아닌 이전의 계산한 값을 재사용할 수 있어 연산의 양이 무한히 절반으로 줄어드는 것이다.

우리는 임의의 $x_i$ 를 $\omega_N = \cos(\frac{2\pi}{N}) + i\cdot \sin(\frac{2\pi}{N})$ 로 설정했던것을 기억하자. 정말 자연스레 다음의 식도 성립을 한다. $\omega_N^{2k} = \omega_{\frac{N}{2}}^{k}$

조금 더 풀어서 보도록 하자. 만일 $N = 8$ 이라고 하면, 다음과 같을 것이다.

A(\omega^0_8) = P_e(\omega^0_8) + \omega^0_8 \cdot P_o(\omega^0_8) = P_e(\omega^0_4)+\omega^0_8\cdot P_o(\omega^0_4) \\ A(\omega^1_8) = P_e(\omega^2_8) + \omega^1_8 \cdot P_o(\omega^2_8) = P_e(\omega^1_4)+\omega^1_8\cdot P_o(\omega^1_4) \\ A(\omega^2_8) = P_e(\omega^4_8) + \omega^2_8 \cdot P_o(\omega^4_8) = P_e(\omega^2_4)+\omega^2_8\cdot P_o(\omega^2_4) \\ \vdots \\ A(\omega^6_8) = P_e(\omega^{12}_8) + \omega^6_8 \cdot P_o(\omega^{12}_8) = P_e(\omega^6_4)+\omega^6_8\cdot P_o(\omega^6_4) \\ A(\omega^7_8) = P_e(\omega^{14}_8) + \omega^7_8 \cdot P_o(\omega^{14}_8) = P_e(\omega^7_4)+\omega^7_8\cdot P_o(\omega^7_4)

이렇게 보면은 별 의미가 없어보이지만 우리가 임의의 값을 $\omega_N = \cos(\frac{2\pi}{N}) + i\cdot \sin(\frac{2\pi}{N})$ 로 설정했다는 것을 기억하자. $\omega_4$ 를 예시로 들자면, $\omega_4^4 = e^{\frac{2\pi}{4}i \cdot 4} = e^{2\pi i} = 1$ 임을 알 수 있다. 즉, 다음과 같다는 의미이다.

P_e(\omega^4_4)+\omega^4_8\cdot P_o(\omega^4_4) = P_e(\omega^0_4)+\omega^4_8\cdot P_o(\omega^0_4) \\ P_e(\omega^5_4)+\omega^5_8\cdot P_o(\omega^5_4) = P_e(\omega^1_4)+\omega^5_8\cdot P_o(\omega^1_4) \\ P_e(\omega^6_4)+\omega^6_8\cdot P_o(\omega^6_4) = P_e(\omega^2_4)+\omega^6_8\cdot P_o(\omega^2_4) \\ P_e(\omega^7_4)+\omega^7_8\cdot P_o(\omega^7_4) = P_e(\omega^3_4)+\omega^7_8\cdot P_o(\omega^3_4)

$\omega_4^5 = \omega_4^4 \cdot \omega_4^1$

여기서 끝이 아니다. 우리는 다음과 같이 또 표현할 수 있다.
~~끝이 없어 흑흑~~

P_e(\omega_4^0) = P_e(\omega_2^0)+ \omega_4^0 \cdot P_o(\omega_2^0) \\ P_e(\omega_4^1) = P_e(\omega_2^2)+ \omega_4^1 \cdot P_o(\omega_2^2) \\ P_e(\omega_4^2) = P_e(\omega_2^4)+ \omega_4^2 \cdot P_o(\omega_2^4) \\ P_e(\omega_4^3) = P_e(\omega_2^6)+ \omega_4^3 \cdot P_o(\omega_2^6)

이는 Odd Poly에 대해서도 마찬가지 이다.

P_o(\omega_4^0) = P_e(\omega_2^0)+ \omega_4^0 \cdot P_o(\omega_2^0) \\ P_o(\omega_4^1) = P_e(\omega_2^2)+ \omega_4^1 \cdot P_o(\omega_2^2) \\ P_o(\omega_4^2) = P_e(\omega_2^4)+ \omega_4^2 \cdot P_o(\omega_2^4) \\ P_o(\omega_4^3) = P_e(\omega_2^6)+ \omega_4^3 \cdot P_o(\omega_2^6)

이쯤 되면 규칙성이 보인다.

$\omega_2^2 = 1$ 이며, $\omega_2^0 = \omega_2^2 = \omega_2^4 = \omega_2^6$ 임을 유추할 수 있다.

물론 단순 연산의 양은 동일하다고 할 수 있지만, 크나큰 차이점이 하나 생긴다. 바로 값의 재사용이 일어난다는 것이다. 이러한 성질을 이용하여 우리는 $O(N^2)$ 만큼의 연산을 $O(\log{N})$ 내에서 해결할 수 있게 된 것이다.
이후의 곱의 연산은 간단하다. $(\omega, A(\omega)), (\omega, B(\omega))$ 를 알고있으니, $C(x) = A(x) \cdot B(x)$ 라 할 때 $(\omega, A(\omega) \cdot B(\omega))$ 를 구하면 될 것이다.