[JS] - 카카오 인턴 [BFS]

문제

문제링크

• 이 문제는 주어진 nxn 보드에 도로를 건설하는 것이 목표다. 최단거리, 최소비용으로 도착점에 도달해야한다.

• 최단거리로 가야하니 왔던 길을 되돌아가면 안된다.

• 최소비용으로 가야하니 방향을 최소한으로 틀어야한다. (직/후진은 100원, 좌/우회전은 600원)
  모든 경로를 기록해야하니 알맞은 저장방식이 필요하다.

• BFS(Breadth First Search) 탐색 방식을 이용한 풀이를 정리해보자.

문제 핵심

저장할 정보

[x좌표, y좌표, 최근방향, 현재까지 비용]
x, y, D, price
[1, 0, 0, 100]

1. 방문할 칸의 x좌표
2. 방문할 칸의 y좌표
3. 해당칸을 방문한 방향
4. 해당칸까지의 경주로 건설 비용

방향 이미지

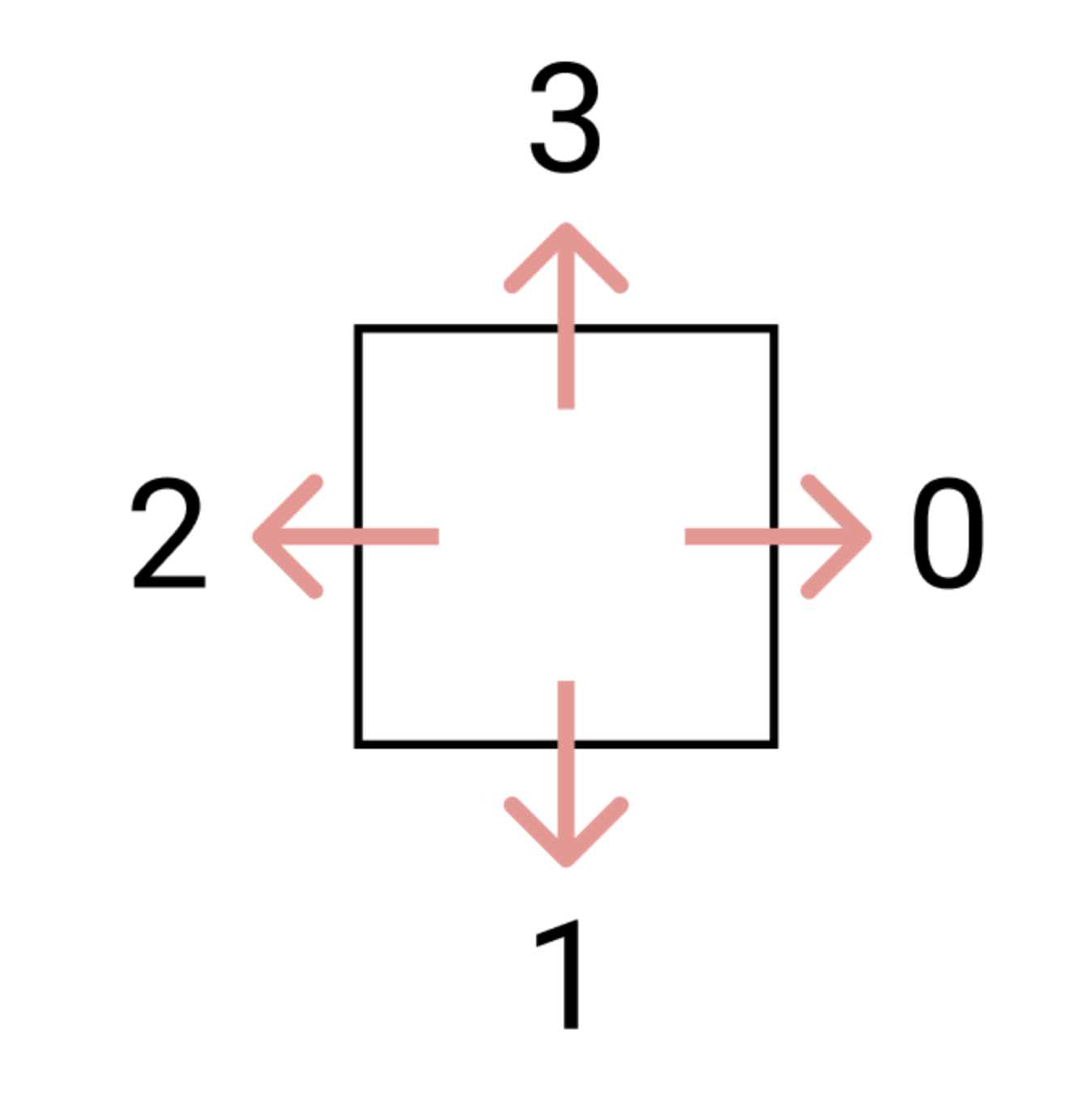
되돌아가는것을 제외한 방향 ~!!

방향이 0이었다면 다음 방향이 2가 되면 안된다
방향이 1이었다면 다음 방향이 3이 되면 안된다
방향이 2였다면 다음 방향이 0이 되면 안된다
방향이 3이었다면 다음 방향이 1이 되면 안된다.

k = [0, 1, 3]
D_new = (D_old + k) % 4

D_old = 0;
D_new = (0 + 0) % 4 = 0; (k=0)
D_new = (0 + 1) % 4 = 1; (k=1)
D_new = (0 + 3) % 4 = 3; (k=3)
D_new = [0, 1, 3];
0의 반대 방향인 2는 나오지 않는다.

소스코드

// 방향을 생각하는게 진짜 어렵다..~!
        // 1. 방문할 칸의 x좌표
        // 2. 방문할 칸의 y좌표
        // 3. 해당칸을 방문한 방향
        // 4. 해당칸까지의 경주로 건설 비용    
        function solution(board) {
        let answer = 0;   
        const n = board.length
        const Q = [[0,0,'',0]]
        const directionAdds = [0, 1, 3] 
        // 범위 조건
        const checkPush = ([x,y]) => {
            return x >= 0 && x < n && y >= 0 && y < n && !(x === 0 && y === 0) && board[x][y] !== 1
        } 
        while (Q.length) {
            let [x,y,direction,price] = Q.shift();
            //보드판에서 현재 좌표에 해당하는 칸의 값이 0이거나 비용보다 크면 비용으로 대체한다.
            //항상 더 적은 비용으로 대체해야한다
            if (board[x][y] >= price || board[x][y] === 0) {
                board[x][y] = price
                directionAdds.forEach(k => {
                    let D = (direction+k)%4;
                    let a = 0;
                    //각방향 x,y 좌표 업데이트
                    //let a = D === 0 ? x+1 : (D === 2 ? x-1 : x)
                    if(D === 0){
                        a = x+1;
                    }else if(D === 2){
                        a = x-1;
                    }else{
                        a = x;
                    }
                    let b = 0;
                    //let b = D === 1 ? y+1 : (D === 3 ? y-1 : y)
                    if(D === 1){
                        b = y+1;
                    }else if(D === 3){
                        b = y-1;
                    }else{
                        b = y;
                    }
                    // k === 0 이란 말은 방향을 변화지 않고 그대로 가겟다는것
                    if (checkPush([a,b])) {
                        //Q.push([a,b, D, k === 0 || direction === '' ? price + 100 : price + 600])
                        if(k === 0 || direction === ''){
                            Q.push([a,b,D,price + 100]);
                        }else{
                            Q.push([a,b,D,price + 600]);
                        }
                    }
                })
        }
        }
        console.log(board);
        // 맨끝 좌표 도착지점 출력
        return board[n-1][n-1]
    }