색종이 만들기 - 재귀 함수를 이용한 분할정복

문제

아래 <그림 1>과 같이 여러개의 정사각형칸들로 이루어진 정사각형 모양의 종이가 주어져 있고, 각 정사각형들은 하얀색으로 칠해져 있거나 파란색으로 칠해져 있다. 주어진 종이를 일정한 규칙에 따라 잘라서 다양한 크기를 가진 정사각형 모양의 하얀색 또는 파란색 색종이를 만들려고 한다.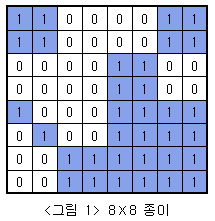
전체 종이의 크기가 N×N(N=2k, k는 1 이상 7 이하의 자연수) 이라면 종이를 자르는 규칙은 다음과 같다.

전체 종이가 모두 같은 색으로 칠해져 있지 않으면 가로와 세로로 중간 부분을 잘라서 <그림 2>의 I, II, III, IV와 같이 똑같은 크기의 네 개의 N/2 × N/2색종이로 나눈다. 나누어진 종이 I, II, III, IV 각각에 대해서도 앞에서와 마찬가지로 모두 같은 색으로 칠해져 있지 않으면 같은 방법으로 똑같은 크기의 네 개의 색종이로 나눈다. 이와 같은 과정을 잘라진 종이가 모두 하얀색 또는 모두 파란색으로 칠해져 있거나, 하나의 정사각형 칸이 되어 더 이상 자를 수 없을 때까지 반복한다.
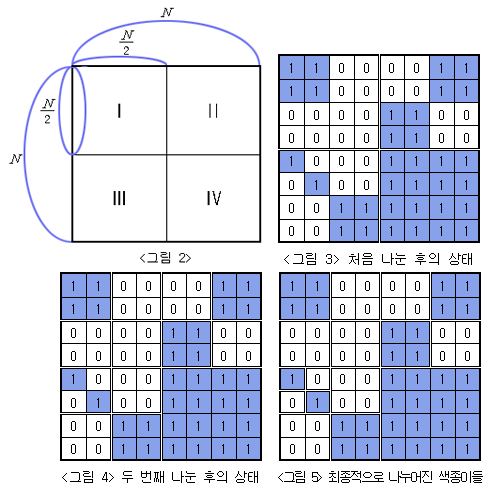위와 같은 규칙에 따라 잘랐을 때 <그림 3>은 <그림 1>의 종이를 처음 나눈 후의 상태를, <그림 4>는 두 번째 나눈 후의 상태를, <그림 5>는 최종적으로 만들어진 다양한 크기의 9장의 하얀색 색종이와 7장의 파란색 색종이를 보여주고 있다.

입력
첫째 줄에는 전체 종이의 한 변의 길이 N이 주어져 있다. N은 2, 4, 8, 16, 32, 64, 128 중 하나이다. 색종이의 각 가로줄의 정사각형칸들의 색이 윗줄부터 차례로 둘째 줄부터 마지막 줄까지 주어진다. 하얀색으로 칠해진 칸은 0, 파란색으로 칠해진 칸은 1로 주어지며, 각 숫자 사이에는 빈칸이 하나씩 있다.

출력
첫째 줄에는 잘라진 햐얀색 색종이의 개수를 출력하고, 둘째 줄에는 파란색 색종이의 개수를 출력한다.

풀이

조건이 만족하지 않는 경우(색상이 모두 같은 경우가 아닌 경우)는 4분의 1로 분할한다.

4분할 시 재귀법을 사용하고, 전달인자로는 그 사분면의 가장 왼쪽 위의 좌표와 크기를 넣어준다.

조건이 만족하는 경우(하나의 색상으로만 구성되는 경우)는 해당 색상의 값을 카운팅한다.

참고로 트리의 자식 노드가 4개씩 분할하는 방법을 쿼드 트리라고 한다.
우린 작게 분할한 색종이 안에서 같은 색인지를 판단해 같지 않다면 다시 나누는 과정을 반복할 것이다.

자, 일단 처음 전체 종이의 크기가 N×N이다.
한 번 사분할하면 종이의 가로세로 길이는 각각 N//2가 된다.

위를 토대로 하면 한 사분면의 기준이 되는 사분면의 가장 첫번째 좌표, 즉 왼쪽 최상단의 좌표는 다음과 같이 수식화됨을 이해할 수 있다.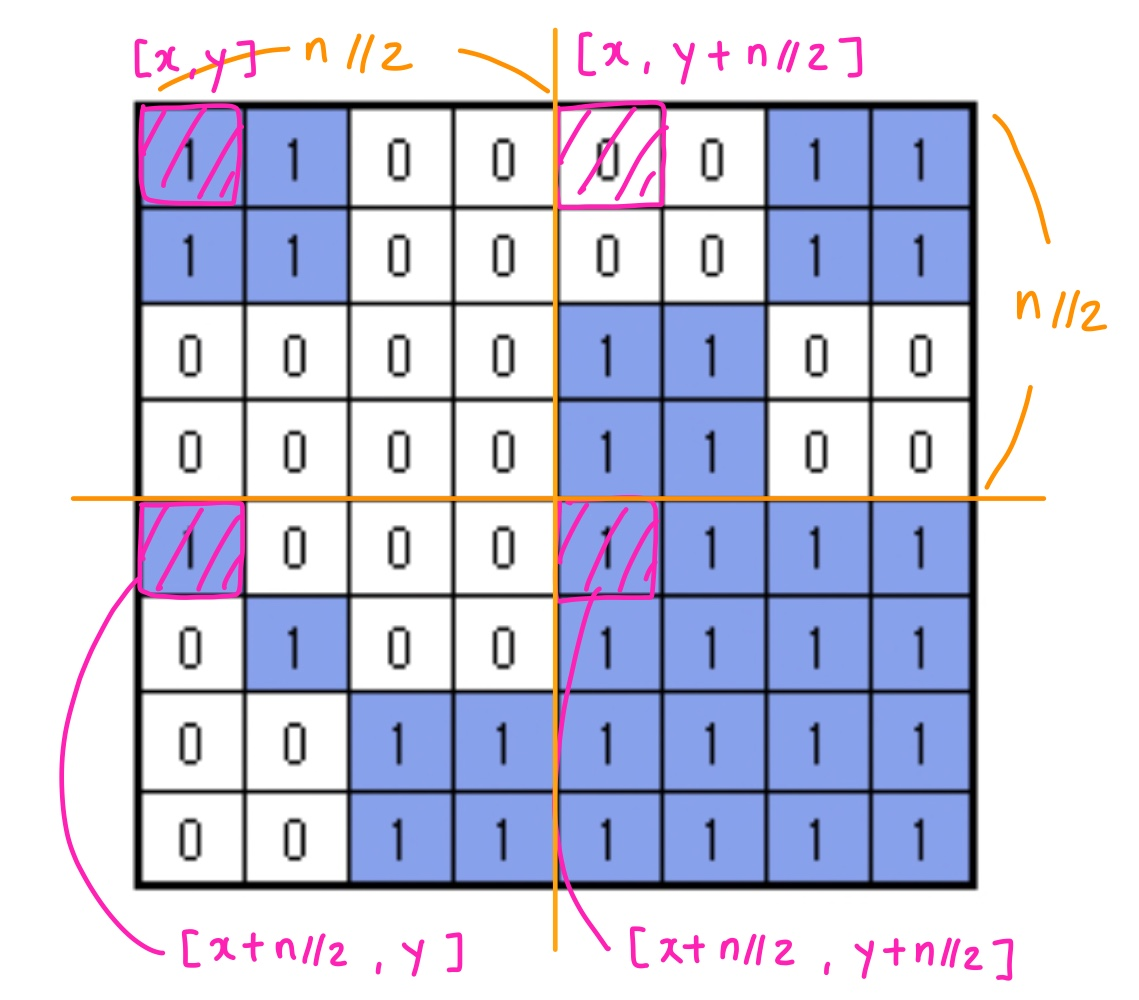 이 블로그에서 도움을 받았다. https://chaewsscode.tistory.com/95

아래의 코드는 정답이다.

import sys
input = sys.stdin.readline
N = int(input())
board = list( list(map(int, input().split())) for _ in range(N) )
blue = 0
white = 0

def recur(x, y, N):
    global white, blue
    color = board[x][y]
    for row in range(x, x+N):
        for col in range(y, y+N):
            if color != board[row][col]:
                recur(x,      y,      N//2) # 1사분면
                recur(x,      y+N//2, N//2) # 2사분면
                recur(x+N//2, y,      N//2) # 3사분면
                recur(x+N//2, y+N//2, N//2) # 4사분면
                return
    if color==0:
        white += 1
    else:
        blue += 1

recur(0, 0, N)
print(white, blue, sep='\n')

전체 색종이 board = [list(map(int, input().split())) for _ in range(N)]에서 얻을 수 있는 정보값 board[x][y]는 결국 색깔의 여부일 것이다.
고로 board[x][y]는 color 라는 변수로 선언하여 활용한다.

남의 풀이를 분석할 때 초입에서 blue, white 두 변수가 모두 값이 0인 점이 의문이었는데 이는 for문의 대상이 되는 범위 안에서의 blue와 white의 개수를 세는 변수이고 종이를 자르는 수행은 어떤 색인지의 구별 없이 걍 지금 세고 있는 색과 같은 색인지 아닌지의 여부가 중요한 것이므로 그리 혼란스러울 것도 없었당 ㅋ

분할 정복은
기본적으로 2로 나누는 경우가 많은데, 원리가 다음과 같다.

대상을 계속해서 2분할, 또 2분할, 또 2분할하여 대상의 정보가 더 이상 2로 나눌 수 없는 자연수인 1이 될 때까지 재귀 호출을 하도록 한다.

간단한 분할 정복 문제들에 대한 풀이법은 대강 다음과 같은 꼴을 하곤 한다.

def recur(x, y, 인자.., N):
.
.
	check = matrix[x][y]
.
.
	for i in range(x, x+N.. y어쩌고, N) :
            if 2분할하는 조건:
                recur(x,   y..   N//2) # 1사분면
                recur(x,   y..   N//2) # 2사분면
                recur(x+N//2,   y..   N//2) # 3사분면
                recur(x+N//2,   y..   N//2) # 4사분면
                return
    .
    .
    if check == '0':
        answer += '0'
    else:
        answer += '1'
    return

recur(0, .., N)

기본 분할정복 문제인 쿼드 트리 문제(https://www.acmicpc.net/problem/1992)의 답안도 위와 개똑같은 모습을 하고 있다. 이게 기본의 틀인 것 같다.
혹은

while N != 0:
	N -= 1
    .
    .
            if 2분할하는 조건:
                어저고저쩌고 할 일 수행 N*2 # 1사분면
            if 2분할하는 조건:
                어저고저쩌고 할 일 수행 N*2 # 2사분면
            if 2분할하는 조건:
                어저고저쩌고 할 일 수행 N*2 # 3사분면
            if 2분할하는 조건:
                어저고저쩌고 할 일 수행 N*2 # 4사분면
     return
    .
    .

recur(0, .., N)

Z문제(https://www.acmicpc.net/problem/1074)다.

근데 디버깅을 해봐도 너무 어렵다.ㅇ....
아래는 대강 색종이 만들기 풀이에 대한 분석이다.

import sys
input = sys.stdin.readline
N = int(input())
board = list( list(map(int, input().split())) for _ in range(N) )
blue = 0
white = 0

def recur(x, y, N):
    global white, blue
    color = board[x][y]             # 현재 내가 들고있는 색깔(즉, 직전의 for문 때 확인한 색깔)
    for row in range(x, x+N):       # 처음 시작하는 종이의 가로 변: 0부터 N까지.
        for col in range(y, y+N):   # 처음 시작하는 종이의 세로 변: 0부터 N까지.
            check = board[row][col] # 지금(이번 for문) 확인할 종이칸 좌표. 뭔 색깔인지 확인. 
            if color != check:      # 색이 이어지지 않고 달라졌다면 잘라줄 것이다!
                recur(x, y, N//2)           # 1. 현재 종이의 1사분면으로 가 색깔 확인하는 수행. 
                recur(x, y+N//2, N//2)      # 3. 현재 종이의 2사분면으로 가 색깔 확인하는 수행. 
                recur(x+N//2, y, N//2)      # 5. 현재 종이의 3사분면으로 가 색깔 확인하는 수행. 
                recur(x+N//2, y+N//2, N//2) # 7. 현재 종이의 4사분면으로 가 색깔 확인하는 수행.
                # 9. 길이가 N//2이 되어 처음에서부터 4분할 된 종이 4개를 한 번 싹 돌았다. 이제 그것들을 길이가 N//2//2인 종이들로 한 번씩 더 난도질해서 총 16분할 된 종이들도 돌아가며 확인한다. 처음으로 올라서 아까처럼 recur() 4개를 쭉 훑고 내려올 것.
                return
    # 2. 4. 6. 8. 길이가 N//2이 된 사분면으로 가 한 바퀴 쭉 다 돌고 색깔 확인하는 수행을 마침.
    #             방금 내가 자른 종이가 무슨 색인지 확인 후 수 적립 후 다음 사분면으로 감.
    if color==0:
        white += 1
    else:
        blue += 1

recur(0, 0, N)
print(white, blue, sep='\n')

그니까 결국 저 4개의 recur()가 꼭 하나의 거대한 재귀함수 묶음같이 작용하는 것 같다.